Толстые кучи

Основные операции

Операция make-heap заключается в инициализации счетчиков. Трудоемкость .

Операция FindMin возвращает указатель на минимальный элемент. Трудоемкость .

Операция Insert(key). Чтобы выполнить эту операцию, делаем новый элемент отдельным деревом и выполняем процедуру вставки нового элемента ранга в корневой счетчик. После этого, если необходимо, корректируем значение указателя на минимальный элемент.

Операция уменьшения ключа DecreaseKey. Чтобы выполнить эту операцию, поступим следующим образом. Пусть — узел, на который указывает указатель . Вычитаем из ключа узла . Если новый ключ меньше минимального ключа кучи 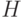, обмениваем ключ элемента с ключом минимального элемента. Новых нарушений операция не создаст. Пусть — ранг . Если — нарушаемый узел, добавляем как новое -ранговое нарушение инкрементированием -й цифры счетчика нарушений. Трудоемкость .

Операция DeleteMin выполняется следующим образом. Удаляем поддерево с корнем в минимальном узле из леса. Минимальность этого элемента гарантирует нам, что среди его детей нарушений порядка кучи не было. То есть нет необходимости работать со счетчиком нарушений. Затем вставляем в кучу все деревья с корнями, расположенными в детях удаляемого узла. Очевидно, что новый минимальный ключ — либо в корне дерева леса, либо в нарушенном узле. Выполняем поиск нового минимального элемента среди корней деревьев и нарушенных узлов.

Если минимальный элемент оказался в нарушенном узле, то обмениваем его с элементом, хранимым в корне этого дерева, корректируя корневой счетчик, если это необходимо. После замены новый минимум — в корне дерева леса. Этот корень будет новым минимальным узлом. Трудоемкость операции равна .

Операция удаления элемента. Выполняется с помощью 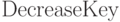и затем . Трудоемкость операции .

Операция Meld(h1, h2). Выполняется следующим образом. Первый шаг — фиксируются все нарушения в куче с меньшим максимальным рангом (разрывая связь произвольно). Не уменьшая общности, считаем, что эта куча — . Пройти по счетчику нарушений от младшей цифры к старшей, пропуская цифры со значением . Для -й цифры делаем операцию фиксирования на каждой цифре, показываемой прямым указателем 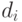, если эта цифра имеет значение 2. Затем, если , фиксируем 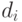. Если , преобразуем это -ранговое нарушение в -ранговое нарушение, как при фиксировании, используя -рангового брата нарушенного узла вместо (несуществующего) другого -рангового нарушения.

Как только не будет содержать каких-либо нарушений, нужно вставить корни из корневого счетчика в корневой счетчик 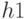инкрементированием соответствующих цифр. Если минимальный узел содержит меньший ключ, чем минимальный узел 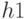, следует установить новым минимальным узлом 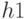минимальный узел . Затем нужно вернуть модифицированную кучу 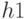в качестве результата . Трудоемкость операции равна .

Операция DeleteViolation. Для освобождения кучи от нарушений достаточно выполнить операторы

Основываясь на описанной выше реализации толстой кучи, получаем следующий результат. В толстых кучах операции и 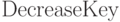выполняются за время , а и — за время .

Замечание. Существует альтернативное представление избыточных счетчиков. Вместо одной записи на цифру можно использовать одну запись на блок одинаковых цифр. Инкрементирование любой цифры можно выполнить за время , используя это альтернативное представление. Преимущество такого представления — возможность расширить счетчик на произвольное число одинаковых цифр за постоянное время.

Г.Бродал описывает кучевидную структуру, которая теоретически лучше, чем толстые кучи, так как их временная оценка для — в худшем случае. Структура Бродала, однако, намного сложнее толстых куч.