НОУ ИНТУИТ | Защита информации в электронных платежных системах. Лекция 19: Будущее электронной коммерции

Учитесь и получайте официальные документы БЕСПЛАТНО. Вы можете поддержать наш проект.

Регистрация Вход

Твой путь к знаниям!

Опубликован: 24.10.2016 | Уровень: для всех | Доступ: платный

|

Вам нравится? Нравится 27 студентам

| Поделиться |

Поддержать программу

Приложение 5

Конечные поля. Криптосистема на основе эллиптических уравнений

Эллиптические кривые суть математический объект, который может быть определен над любым полем. В криптографии обычно используются конечные поля. Для точек на эллиптической кривой вводится операция сложения, которая играет ту же роль, что и операция умножения в криптосистеме RSA.

Многочисленные исследования показали, что криптосистемы на основе эллиптических кривых превосходят другие системы с открытым ключом по двум важным параметрам: степени защищенности в расчете на каждый бит ключа и быстродействию при программной и аппаратной реализациях.

Математические основы

Группа. Группой G называется множество элементов a, b, g, ..., обладающее следующими свойствами.

Для элементов множества G определена некоторая операция двух переменных, записываемая в виде a + b = g или в виде ab = g; в первом случае операцию условно называют сложением, во втором - умножением.

На множестве G выполняются следующие законы:

в результате применения операции к двум любым элементам группы также получается элемент группы (свойство замкнутости);
для любых трех элементов группы справедливо (a+b) + g = a + (b + g), если операция является сложением; или (ab)g = a (bg) если операция является умножением (ассоциативный закон);
в группе существует единичный элемент, который обозначается как 0 для сложения, при этом для любого элемента a группы справедливо 0 + a = a + 0 = a; либо как 1 для умножения, при этом для любого элемента a группы справедливо 1a = a1 = a;
каждый элемент a группы обладает обратным элементом, который обозначается как (–a) для сложения, при этом a + (–a) = (–a) + a = 0; либо как $a^{–1}$ для умножения, при этом $aa^{–1} = a^{–1}a = 1$ .

Если для любых элементов a, b группы выполняется коммутативный закон, т.е. справедливо равенство a + b = b + a для сложения или ab = ba для умножения, группа называется коммутативной или абелевой.

Число элементов группы называется порядком группы.

Абелева группа относительно операции сложения называется аддитивной абелевой группой, абелева группа относительно операции умножения называется мультипликативной абелевой группой.

Некоторое подмножество группы G называется подгруппой, если оно удовлетворяет всем свойствам группы.

Конечная группа, которая состоит из степеней $1, g, g^2, g^3, \ldots$ одного из ее элементов g, называется циклической группой. При этом наименьшее целое число e такое, что g^e = 1 , называется порядком элемента g.

Конечное поле. Конечным полем или полем Галуа GF (p) называется конечное множество из p (где p = q^n , q - простое, n - натуральное) элементов a, b, g, …, обладающее следующими свойствами:

для элементов множества GF (p) определены две операции двух переменных, записываемые в виде a + b = g и в виде ab = g; первую операцию условно называют сложением, вторую - умножением;
на множестве GF (p) выполняются следующие законы:
- в результате применения операции сложения или умножения к двум любым элементам группы также получается элемент группы (свойство замкнутости),
- для любых трех элементов для операции сложения справедливо (a+b) + g = a + (b + g), для операции умножения справедливо (ab)g = a (bg) (ассоциативный закон),
- для любых трех элементов справедливо (a+b)g = ag + bg,
- в GF (p) существует нулевой элемент, который обозначается как 0, при этом для любого элемента a группы справедливо 0a = 0, 0 + a = a + 0 = a,
- в GF (p) существует единичный элемент, который обозначается как 1, при этом для любого элемента a группы справедливо 1a = a1 = a,
- каждый элемент a конечного поля обладает обратным аддитивным и мультипликативным элементами, которые обозначаются как (–a) для сложения, при этом a + (–a) = (–a) + a = 0; либо как a–1 для умножения, при этом $aa^{–1} = a^{–1}a = 1$ ;
в GF (p) все ненулевые элементы поля могут быть представлены в виде степени примитивного элемента w, т.е. в виде . Таким образом, поле может быть записано в виде

$GF (p) = \{0, w^0, w^1, w^2, \ldots, w^{p – 2}\},$

где		=	$1, w^1 = w, w^{p – 1}= 1, w^p= w \ldots ;$
		-	множество всех ненулевых элементов поля GF (p), образующее абелеву группу порядка p – 1.

Допустим, p = 5 — простое. Тогда целые числа 0, 1, 2, 3, 4 образуют поле GF (5), при этом все операции сложения и умножения выполняются по модулю 5. Примеры выполнения различных операций в рассматриваемом поле:

2 + 3 = 0, 4 + 4 = 3;

4 – 1 = 4 + (–1) = 4 + 4 = 3; 1 – 3 = (5 + 1) – 3 = 3;

2 * 3 = 1, 4 * 3 = 2;

1/2 = (5 + 1)/3 = 2, 2/3 = (2 * 5 + 2)/3 = 4;

2–1 = 3, 4–1 = 4.

Группа точек эллиптической кривой. Рассмотрим приведенную на рис. 1 эллиптическую кривую Е, соответствующую уравнению

y^2 + y = x^3 – x^2 .

Рис. 1. Группа из 5 точек эллиптической кривой Е, соответствующей приведенному ниже уравнению

y^2 + y = x^3 – x^2 , О — бесконечно удаленная точка

На этой кривой лежат только четыре точки, координаты которых являются целыми числами. Это точки

А (0, 0), В (1, –1), С (1, 0) и D (0, –1).

Для определения операции сложения на группе точек эллиптической кривой будем считать, что:

на плоскости существует бесконечно удаленная точка О E, в которой сходятся все вертикальные прямые;
касательная к кривой пересекает точку касания Р 2 раза (это допущение становится понятным, если вспомнить, что касательная PR суть предельное положение секущей PM при стремлении точки М к точке Р), как показано на рис. 2.

Рис. 2. Касательная к эллиптической кривой

Теперь можно сформулировать правила сложения точек P, Q E:

проведем прямую линию через точки P и Q, найдем третью точку S пересечения этой прямой с кривой Е;
проведем через точку S вертикальную прямую до пересечения с кривой E в точке T;
искомая сумма равна P + Q = T.

Процесс нахождения суммы точек эллиптической кривой графически изображен на рис. 3.

Рис. 3. Сложение точек на эллиптической кривой. P + Q = T

Применив это правило к группе точек $G = \{A, B, C, D, О\}$ , получим:

A + A = B, A + B = C, A + C = D, A + D = О

или

2А = В, 3А = С, 4А = D, 5А = О, 6А = А.

Для любых точек P, Q G справедливо P + Q = Q + P. Для любой точки P G справедливо P + О = P, иными словами, точка О суть аддитивный единичный элемент группы G.

Пример аддитивной абелевой группы точек приведен на рис. 4.

Рис. 4. Аддитивная абелева группа {A, B, C, D, О} на эллиптической кривой

Эллиптическая кривая над GF (p). В реальных криптосистемах используется уравнение

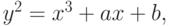
y^2 = x^3 + ax + b,

где	a, b		$GF (p), 4a^3 + 27b^2 \ne 0 (mod p) + ax,$
	p > 3	-	простое.

Группа E (GF (p)) состоит из всех точек (x, y),

где x, y GF (p), удовлетворяющих уравнению, и бесконечно удаленной точки О.

Определенная над точками из E (GF (p)) операция сложения алгебраически может быть описана следующим образом.

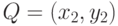Допустим, P = (x_1, y_1) и Q = (x_2, y_2) .

Тогда P + Q = (x_3, y_3) ,

где

$X_3 = \lambda^2 – x_1 – x_2$ ;

$Y_3 = \lambda (x_1 – x_3 – y_1)$ ,

а

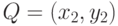Число суть угловой коэффициент секущей, проведенной через точки P = (x_1, y_1) и Q = (x_2, y_2) .

При P = Q секущая превращается в касательную, чем и объясняется наличие двух формул для вычисления .

Для любой точки P E (GF (p)) справедливо P + O = O + P = P.

Если P = (x, y) E (GF (p)), то (x, y) + (x, –y) = O.

Точка (x, –y) E (GF (p)) является обратным элементом по отношению к P и обозначается –P.

Задача, которую вынужден решать противник при использовании криптосистемы на базе эллиптических уравнений, своего рода задача "дискретного логарифмирования на эллиптической кривой", формулируется следующим образом.

Даны точки P и Q на эллиптической кривой порядка r, где r - число точек на кривой. Необходимо найти единственную точку x - такую, для которой P = xQ.

Допустим, $p = 5, a = b = 1, 4a^3 + 27b^2 = 4 + 4 = 8 \ne 0$ .

Рассмотрим эллиптическую кривую

E: y^2 = x^3 + x + 1.

Вид кривой, соответствующей такому уравнению, показан на рис. 5.

Рис. 5. Эллиптическая кривая, соответствующая показанному ниже уравнению

y^2 = x^3 + x + 1

E (GF (5)) состоит из следующих точек, представленных на рис. 6:

P = (0, 1), 2P = (4, 2), 3Р = (2, 1), 4Р = (3, 4), 5Р = (3, 1),

6Р = (2, 4), 7Р = (4, 3), 8Р = (0, 4), 9Р = O,

при этом 10Р = Р.

Рис. 6.

На рис. 6 показана аддитивная группа на E (Z_5)

Алгоритм электронной подписи на основе эллиптических кривых ECDSA. Алгоритм ECDSA (Elliptic Curve Digest Signature Algorithm) принят в качестве стандартов ANSI X9F1 и IEEE P1363. В Германии ECDSA является государственным стандартом. В России разработан ГОСТ на основе ECDSA.

Алгоритм генерации ключей.

Выбираем эллиптическую кривую Е, определенную на . Число точек в должно делится на большое целое n.
Выбираем точку $P \in E (Z_p)$ порядка n.
Выбираем случайное число $d \in [1, n – 1]$ .
Вычисляем .
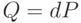Секретным ключом объявляем d, открытым - (E, P, n, Q).

Алгоритм формирования подписи под сообщением M.

Выбираем случайное число $k \in [1, n – 1]$ .
Вычисляем и .
Если $r \ne 0$ , переходим к шагу 3, в противном случае возвращаемся к шагу 1.
Вычисляем .
Вычисляем .
Если $s \ne 0$ , переходим к шагу 5, в противном случае возвращаемся к шагу 1.
Подписью под сообщением M является пара целых чисел (r, s).

Примечания.

В качестве хеш-функции h (x) на шаге 4 в стандартах ANSI X9F1 и IEEE P1363 используется SHA-1.
При r = 0 результат вычисления s не зависит от секретного ключа d.
При s = 0 необходимого для проверки подписи числа $s^{–1} mod n$ не существует.

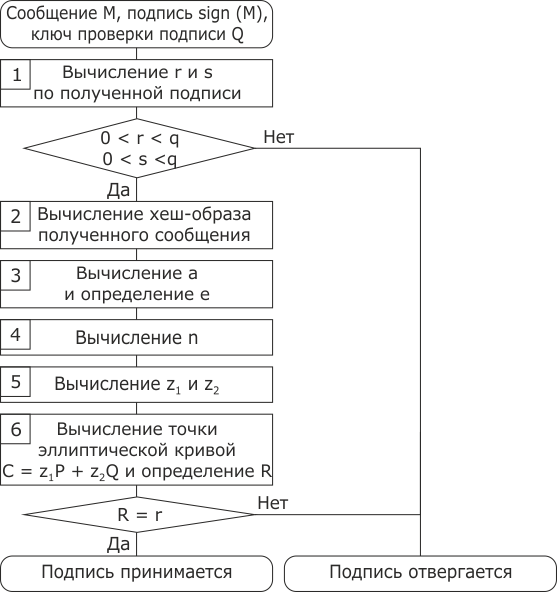
Алгоритм проверки подписи (r, s) сообщения M с помощью открытого ключа (E, P, n, Q).

Если r и s - целые числа, принадлежащие интервалу [1, n – 1], переходим к шагу 2, в противном случае - результат проверки отрицательный (подпись отвергается).
Вычисляем $w = s^{–1} mod n$ и h (M).
Вычисляем и .
Вычисляем и .
Подпись верна в том и только том случае, когда n = r.

Новый Российский стандарт цифровой подписи*
$V_{256}$	множество всех двоичных векторов длиной 256 бит
$V_{\infty}$	множество всех двоичных векторов произвольной конечной длины
Z	множество всех целых чисел
p	простое число, p > 3
GF (p)	конечное простое поле из p элементов {0, 1, 2, ..., (p – 1)}
b mod p	минимальное неотрицательное число, сравнимое с b по модулю p
h	двоичный вектор, например, двоичный вектор длиной 256 бит может быть представлен в виде $h = (a_{255}, ..., a_1 a_0), a_i \in \{0, 1\}$ , числу a соответствует вектор h, если выполняется равенство $a = \sum a_i 2^i$
M	сообщение, $М \in V_{\infty}$
	конкатенация (объединение) двух двоичных векторов, пусть $h_1 = (a_{255}, \ldots, a_1 a_0), a_i \in \{0, 1\}, h_2 = (b_{255}, \ldots, b_1 b_0), b_i \in \{0, 1\}$ , тогда $(h_1, h_2) = (a_{255}, \ldots, a_1 a_0 b_{255}, \ldots, b_1 b_0)$
a, b	коэффициенты эллиптической кривой
m	порядок группы точек эллиптической кривой
q	порядок подгруппы группы точек эллиптической кривой
O	бесконечно удаленная точка эллиптической кривой
P	точка эллиптической кривой порядка q
d	целое число, ключ формирования подписи
Q	точка эллиптической кривой, ключ проверки подписи
sign (M)	цифровая подпись под сообщением М

* ГОСТ Р34.10-2001. Криптографическая защита информации. Процессы формирования и проверки электронной подписи. М. : Госстандарт России. 2001.

В стандарте процессы генерации пары ключей (формирования и проверки подписи), а также параметров не рассматриваются.

Механизм цифровой подписи включает в себя две основные процедуры:

формирования подписи;
проверки подписи.

На рис. 7 и 8 соответственно приведены схемы процедур формирования и проверки цифровой подписи.

Рис. 7. Схема формирования цифровой подписи

Рис. 8. Схема проверки цифровой подписи

Схема на рис. 7 реализована с использованием операций группы точек эллиптической кривой, определенной над конечным простым полем, а также хеш-функции. Стойкость схемы цифровой подписи основывается на сложности решения задачи дискретного логарифмирования на группе точек эллиптической кривой, а также стойкости используемой хеш-функции. Алгоритм хеширования определен в ГОСТ Р34.11-94.

Разрядность цифровой подписи устанавливается равной 512 битам.

Математические предпосылки

Инвариантом эллиптической кривой Е называется величина J (E), удовлетворяющая тождеству

$J (E) \equiv 1728 * (4a^3/ (4a^3 + 27b^2)) mod p$ .

Коэффициенты a и b эллиптической кривой по известному инварианту J (E) определяются следующим образом:

$a \equiv 3k mod p,$

$b \equiv 2k mod p,$

где $k\equiv J (E)/ (1728 – J (E)) mod p;$

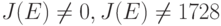$J (E) \ne 0, J (E) \ne 1728$ .

Для абелевой группы порядка m, которую образуют точки эллиптической кривой E, справедливо неравенство:

Точка Q называется точкой кратности k или просто кратной точкой эллиптической кривой Е, если для некоторой точки Р выполняется равенство Q = kP.

Параметрами схемы цифровой подписи являются:

простое число $p > 2^{255}$ , при этом $p^i \ne 1 mod q$ для всех целых i, меньших 32;
эллиптическая кривая Е, задаваемая своим инвариантом или коэффициентами a и b;
целое число m - порядок группы точек эллиптической кривой $Е (m \ne p)$ ;
простое число q - порядок циклической подгруппы группы точек кривой Е, для которого выполняются условия:
$m = nq, n \in Z, n \ge 1$ ,

2254 < q < 2256;
точка $P \ne O$ кривой Е с координатами , удовлетворяющая равенству qP = O.

Ключ формирования подписи - целое число d, удовлетворяющее неравенству 0 < d < q.

Ключ проверки подписи - точка эллиптической кривой Q с координатами (x_Q, y_Q) , удовлетворяющая равенству dP = Q.

Последовательность формирования цифровой подписи сообщения

Последовательность формирования цифровой подписи сообщения $М \in V_{\infty}$

Вычислить хеш-образ h (M) сообщения М.
Вычислить целое число a, двоичным представлением которого является вектор h, и определить $e \equiv a mod q$ . Если е = 0, то определить e = 1.
Сформировать случайное число k, удовлетворяющее условию 0 < k < q.
Вычислить точку эллиптической кривой С = kP и определить $r \equiv x_C mod q$ , где - координата точки С. Если r = 0, то вернуться к шагу 3.
Вычислить значение $s \equiv (rd + ke) mod q$ . Если s = 0, то вернуться к шагу 3.
Вычислить двоичные векторы r и s и определить цифровую подпись sign (M) как конкатенацию двух двоичных векторов (r, s).

Последовательность проверки цифровой подписи

По полученной подписи sign (M) вычислить целые числа r и s. Если выполнены неравенства 0 < r < q, 0 < s < q, то перейти к следующему шагу, в противном случае подпись отвергается.
Вычислить хеш-образ h (M) полученного сообщения М.
Вычислить целое число a, двоичным представлением которого является вектор h, и определить $e \equiv a mod q$ . Если е = 0, то определить e = 1.
Вычислить значение $n \equiv e^{–1} mod q$ .
Вычислить значения $z_1 \equiv sv mod q, z_2 \equiv –rv mod q$ .
Вычислить точку эллиптической кривой и определить $R \equiv x_C mod q$ , где - координата точки С.