| Россия, Пошатово |
Представление множеств. Хеширование
13.2. Хеширование со списками
На хеш-функцию с  значениями можно смотреть как на
способ свести вопрос о хранении одного большого множества
к вопросу о хранении нескольких меньших. Именно, если у нас
есть хеш-функция с
значениями можно смотреть как на
способ свести вопрос о хранении одного большого множества
к вопросу о хранении нескольких меньших. Именно, если у нас
есть хеш-функция с  значениями, то любое множество
разбивается на
значениями, то любое множество
разбивается на  подмножеств (возможно, пустых),
соответствующих возможным значениям хеш-функции. Вопрос
о проверке принадлежности, добавлении или удалении для
большого множества сводится к такому же вопросу для одного
из меньших (чтобы узнать, для какого, надо посмотреть на
значение хеш-функции).
подмножеств (возможно, пустых),
соответствующих возможным значениям хеш-функции. Вопрос
о проверке принадлежности, добавлении или удалении для
большого множества сводится к такому же вопросу для одного
из меньших (чтобы узнать, для какого, надо посмотреть на
значение хеш-функции).
Эти меньшие множества удобно хранить с помощью ссылок; их суммарный размер равен числу элементов хешируемого множества. Следующая задача предлагает реализовать этот план.
13.2.1.
Пусть хеш-функция принимает значения  .
Для каждого значения хеш-функции рассмотрим список всех
элементов множества с данным значением хеш-функции. Будем
хранить эти k списков с помощью переменных
.
Для каждого значения хеш-функции рассмотрим список всех
элементов множества с данным значением хеш-функции. Будем
хранить эти k списков с помощью переменных
Содержание: array [1..n] of T; Следующий: array [1..n] of 1..n; ПервСвоб: 1..n; Вершина: array [1..k] of 1..n;
так же, как мы это делали для k стеков ограниченной суммарной длины. Написать соответствующие программы. (Удаление по сравнению с открытой адресацией упрощается.)
Решение. Перед началом работы надо положить Вершина[i]=0 для всех i=1...k, и связать все места в список свободного пространства, положив ПервСвоб=1 и Следующий[i]=i+1 для i=1...n-1, а также Следующий[n]=0.
function принадлежит (t: T): boolean;
| var i: integer;
begin
| i := Вершина[h(t)];
| {осталось искать в списке, начиная с i}
| while (i <> 0) and (Содержание[i] <> t) do begin
| | i := Следующий[i];
| end; {(i=0) or (Содержание [i] = t)}
| принадлежит := (i<>0) and (Содержание[i]=t);
end;
procedure добавить (t: T);
| var i: integer;
begin
| if not принадлежит(t) then begin
| | i := ПервСвоб;
| | {ПервСвоб <> 0 - считаем, что не переполняется}
| | ПервСвоб := Следующий[ПервСвоб]
| | Содержание[i]:=t;
| | Следующий[i]:=Вершина[h(t)];
| | Вершина[h(t)]:=i;
| end;
end;
procedure исключить (t: T);
| var i, pred: integer;
begin
| i := Вершина[h(t)]; pred := 0;
| {осталось искать в списке, начиная с i; pred -
| предыдущий, если он есть, и 0, если нет}
| while (i <> 0) and (Содержание[i] <> t) do begin
| | pred := i; i := Следующий[i];
| end; {(i=0) or (Содержание [i] = t)}
| if i <> 0 then begin
| | {Содержание[i]=t, элемент есть, надо удалить}
| | if pred = 0 then begin
| | | {элемент оказался первым в списке}
| | | Вершина[h(t)] := Следующий[i];
| | end else begin
| | | Следующий[pred] := Следующий[i]
| | end;
| | {осталось вернуть i в список свободных}
| | Следующий[i] := ПервСвоб;
| | ПервСвоб:=i;
| end;
end;13.2.2.
(Для знакомых с теорией вероятностей.) Пусть хеш-функция
с  значениями используется для хранения множества,
в котором в данный момент
значениями используется для хранения множества,
в котором в данный момент  элементов. Доказать, что
математическое ожидание числа действий в предыдущей задаче
не превосходит
элементов. Доказать, что
математическое ожидание числа действий в предыдущей задаче
не превосходит  , если добавляемый (удаляемый,
искомый) элемент
, если добавляемый (удаляемый,
искомый) элемент  выбран случайно, причем все значения
выбран случайно, причем все значения  имеют равные вероятности (равные
имеют равные вероятности (равные 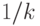 ).
).
Решение. Если  - длина списка, соответствующего
хеш-значению
- длина списка, соответствующего
хеш-значению  , то число операций не превосходит
, то число операций не превосходит  ; усредняя, получаем искомый ответ, так как
; усредняя, получаем искомый ответ, так как  .
.
Эта оценка основана на предположении о равных вероятностях. Однако в конкретной ситуации все может быть совсем не так, и значения хеш-функции могут "скучиваться": для каждой конкретной хеш-функции есть "неудачные" ситуации, когда число действий оказывается большим. Прием, называемый универсальным хешированием, позволяет обойти эту проблему. Идея состоит в том, что берется семейство хеш-функций, причем любая ситуация оказывается неудачной лишь для небольшой части этого семейства.
Пусть 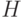 - семейство функций, каждая из которых отображает
множество
- семейство функций, каждая из которых отображает
множество  в множество из
в множество из  элементов (например,
элементов (например,  ). Говорят, что
). Говорят, что 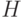 - универсальное
семейство хеш-функций,
если для любых двух различных значений
- универсальное
семейство хеш-функций,
если для любых двух различных значений  и
и  из
множества
из
множества  вероятность события
вероятность события  для
случайной
функции
для
случайной
функции 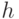 из семейства
из семейства 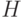 равна
равна 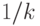 .
(Другими словами,
те функции из
.
(Другими словами,
те функции из 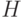 , для которых
, для которых  , составляют
, составляют 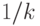 -ую часть всех функций в
-ую часть всех функций в 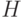 .)
.)
Замечание. Более сильное требование к семейству 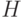 могло бы
состоять в том, чтобы для любых двух различных элементов
могло бы
состоять в том, чтобы для любых двух различных элементов  и
и  множества
множества  значения
значения  и
и  случайной функции
случайной функции 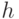 являются
независимыми случайными величинами, равномерно распределенными
на
являются
независимыми случайными величинами, равномерно распределенными
на  .
.
13.2.3.
Пусть  - произвольная последовательность
различных элементов множества
- произвольная последовательность
различных элементов множества  . Рассмотрим количество
действий, происходящих при помещении элементов
. Рассмотрим количество
действий, происходящих при помещении элементов  в множество, хешируемое с помощью функции
в множество, хешируемое с помощью функции 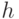 из универсального
семейства
из универсального
семейства 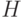 . Доказать, что среднее количество действий
(усреднение - по всем
. Доказать, что среднее количество действий
(усреднение - по всем 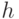 из
из 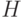 ) не превосходит
) не превосходит  .
.
Решение. Обозначим через  количество элементов
последовательности, для которых хеш-функция равна
количество элементов
последовательности, для которых хеш-функция равна  . (Числа
. (Числа  зависят, конечно, от выбора хеш-функции.)
Количество действий, которое мы хотим оценить, с точностью до
постоянного множителя равно
зависят, конечно, от выбора хеш-функции.)
Количество действий, которое мы хотим оценить, с точностью до
постоянного множителя равно 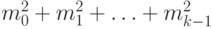 .
(Если
.
(Если  чисел попадают в одну хеш-ячейку, то для этого
требуется примерно
чисел попадают в одну хеш-ячейку, то для этого
требуется примерно  действий.) Эту же сумму
квадратов можно записать как число пар
действий.) Эту же сумму
квадратов можно записать как число пар  , для
которых
, для
которых  . Последнее равенство, если его
рассматривать как событие при фиксированных
. Последнее равенство, если его
рассматривать как событие при фиксированных  и
и  ,
имеет
вероятность
,
имеет
вероятность 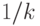 при
при  , поэтому среднее значение
соответствующего члена суммы равно
, поэтому среднее значение
соответствующего члена суммы равно 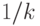 , а для всей суммы
получаем оценку порядка
, а для всей суммы
получаем оценку порядка  , а точнее
, а точнее 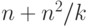 , если
учесть члены с
, если
учесть члены с  .
.
Эта задача показывает, что на каждый добавляемый элемент
приходится в среднем  операций. В этой оценке дробь
операций. В этой оценке дробь 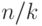 имеет смысл "коэффициента заполнения"
хеш-таблицы.
имеет смысл "коэффициента заполнения"
хеш-таблицы.
13.2.4. Доказать аналогичное утверждение для произвольной последовательности операций добавления, поиска и удаления (а не только для добавления, как в предыдущей задаче).
Указание.
Будем представлять себе, что в ходе поиска, добавления
и удаления элемент проталкивается по списку своих коллег
с тем же хеш-значением, пока не найдет своего двойника
или не дойдет до конца списка. Будем называть  -
-  -столкновением столкновение
-столкновением столкновение 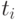 с
с 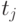 . (Оно
либо произойдет, либо нет - в зависимости от
. (Оно
либо произойдет, либо нет - в зависимости от 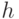 .) Общее
число действий примерно равно числу всех происшедших
столкновений плюс число элементов. При
.) Общее
число действий примерно равно числу всех происшедших
столкновений плюс число элементов. При  вероятность
вероятность  -
-  -столкновения не превосходит
-столкновения не превосходит 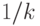 .
Осталось проследить за столкновениями между равными
элементами. Фиксируем некоторое значение
.
Осталось проследить за столкновениями между равными
элементами. Фиксируем некоторое значение  из
множества
из
множества  и посмотрим на связанные с ним операции. Они
идут по циклу: добавление - проверки - удаление -
добавление - проверки - удаление - … Столкновения
происходят между добавляемым элементом и следующими за ним
проверками (до удаления включительно), поэтому общее их
число не превосходит числа элементов, равных
и посмотрим на связанные с ним операции. Они
идут по циклу: добавление - проверки - удаление -
добавление - проверки - удаление - … Столкновения
происходят между добавляемым элементом и следующими за ним
проверками (до удаления включительно), поэтому общее их
число не превосходит числа элементов, равных  .
.
Теперь приведем примеры универсальных семейств.
Очевидно, для любых конечных множеств  и
и  семейство
всех функций, отображающих
семейство
всех функций, отображающих  в
в  , является
универсальным. Однако этот пример с практической точки
зрения бесполезен: для запоминания случайной функции из
этого семейства нужен массив, число элементов в котором
равно числу элементов в множестве
, является
универсальным. Однако этот пример с практической точки
зрения бесполезен: для запоминания случайной функции из
этого семейства нужен массив, число элементов в котором
равно числу элементов в множестве  . (А если мы можем
себе позволить такой массив, то никакого хеширования не
требуется!)
. (А если мы можем
себе позволить такой массив, то никакого хеширования не
требуется!)
Более практичные примеры универсальных семейств могут
быть построены с помощью несложных алгебраических
конструкций. Через 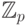 мы обозначаем множество
вычетов по простому модулю
мы обозначаем множество
вычетов по простому модулю  , т.е.
, т.е.  ;
арифметические операции в этом множестве выполняются по
модулю
;
арифметические операции в этом множестве выполняются по
модулю  . Универсальное семейство образуют все линейные
функционалы на
. Универсальное семейство образуют все линейные
функционалы на 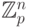 со значениями
в
со значениями
в 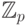 . Более подробно, пусть
. Более подробно, пусть 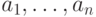 -
произвольные элементы
-
произвольные элементы 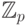 ; рассмотрим
отображение
; рассмотрим
отображение
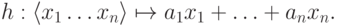
 отображений
отображений  параметризованное
наборами
параметризованное
наборами  .
.13.2.5. Доказать, что это семейство является универсальным.
Указание.
Пусть  и
и  - различные точки пространства
- различные точки пространства 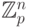 . Какова вероятность того, что случайный
функционал принимает на них одинаковые значения? Другими
словами, какова вероятность того, что он равен нулю на их
разности
. Какова вероятность того, что случайный
функционал принимает на них одинаковые значения? Другими
словами, какова вероятность того, что он равен нулю на их
разности  ? Ответ дается таким утверждением: пусть
? Ответ дается таким утверждением: пусть  - ненулевой вектор; тогда все значения случайного
функционала на нем равновероятны.
- ненулевой вектор; тогда все значения случайного
функционала на нем равновероятны.
В следующей задаче множество 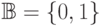 рассматривается как множество вычетов по модулю
рассматривается как множество вычетов по модулю 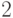 .
.
13.2.6.
Семейство всех линейных отображений из  в
в  является универсальным.
является универсальным.
Родственные хешированию идеи неожиданно оказываются
полезными в следующей ситуации (рассказал Д. Варсанофьев).
Пусть мы хотим написать программу, которая обнаруживала
(большинство) опечаток в тексте,
но не хотим хранить список всех правильных словоформ.
Предлагается поступить так: выбрать некоторое  и набор
функций
и набор
функций  , отображающих русские слова
добавлены запятые в 1,...,N
в
, отображающих русские слова
добавлены запятые в 1,...,N
в  . В массиве из
. В массиве из  битов положим все биты
равными нулю, кроме тех, которые являются значением
какой-то функции набора на какой-то правильной
словоформе. Теперь приближенный тест на правильность
словоформы таков: проверить, что значения всех функций
набора на этой словоформе попадают на места, занятые
единицами. (Этот тест может не заметить некоторых ошибок,
но все правильные словоформы будут одобрены.)
битов положим все биты
равными нулю, кроме тех, которые являются значением
какой-то функции набора на какой-то правильной
словоформе. Теперь приближенный тест на правильность
словоформы таков: проверить, что значения всех функций
набора на этой словоформе попадают на места, занятые
единицами. (Этот тест может не заметить некоторых ошибок,
но все правильные словоформы будут одобрены.)

