| Россия |
Обобщения и применения модели Хопфилда
Алгоритмы разобучения (забывания)
Возможность забывания ненужной, лишней информации является одним из замечательных свойств биологической памяти. Идея приложения этого свойства к искусственной нейросети Хопфилда "удивительно" проста: при запоминании образов обучающей выборки вместе с ними запоминаются и ложные образы. Их-то и следует "забыть".
Соответствующие алгоритмы получили название алгоритмов разобучения. Суть их сводится к следующему.
На первой фазе происходит обучение сети по стандартному правилу
Хебба. Память наполняется истинными образами и множеством ложной
информации. На следующей фазе (фазе разобучения) сети предъявляется
некоторый (случайный) образ  Сеть эволюционирует от
состояния
Сеть эволюционирует от
состояния  к некоторому состоянию
к некоторому состоянию 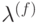 , которое
при большом объеме обучающей выборки чаще всего оказывается ложным.
Теперь матрица связей может быть поправлена, с целью уменьшить глубину
минимума энергии, отвечающего этому ложному состоянию:
, которое
при большом объеме обучающей выборки чаще всего оказывается ложным.
Теперь матрица связей может быть поправлена, с целью уменьшить глубину
минимума энергии, отвечающего этому ложному состоянию:
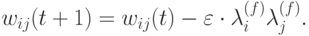
В качестве степени забывания  выбирается некоторое
малое число, что гарантирует незначительное ухудшение полезной памяти,
если состояние
выбирается некоторое
малое число, что гарантирует незначительное ухудшение полезной памяти,
если состояние 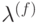 не окажется ложным. После нескольких
"сеансов забывания" свойства сети улучшаются.
не окажется ложным. После нескольких
"сеансов забывания" свойства сети улучшаются.
Данная процедура пока не имеет формального теоретического обоснования, однако на практике приводит к более регулярной энергетической поверхности нейронной сети и к увеличению объема бассейнов притяжения полезных образов.
Непрерывные системы
На предыдущей лекции была рассмотрена классическая модель Хопфилда с двоичными нейронами. Изменение состояний нейронов во времени описывалось детерминированными правилами, которые в заданный момент времени однозначно определяли степень возбуждения всех нейронов сети.
Хопфилд рассматривал модели с непрерывной активационной
функцией  , точнее моделирующей биологический нейрон. В общем
случае это
, точнее моделирующей биологический нейрон. В общем
случае это  -образная или логистическая функция
-образная или логистическая функция

где  — коэффициент, определяющий крутизну сигмоидальной
функции. Если
— коэффициент, определяющий крутизну сигмоидальной
функции. Если  велико,
велико,  приближается к
описанной ранее
пороговой функции. Небольшие значения
приближается к
описанной ранее
пороговой функции. Небольшие значения  дают более пологий
наклон.
дают более пологий
наклон.
Как и для бинарных систем, устойчивость гарантируется, если веса
симметричны, т.е.  и
и  при
всех
при
всех 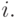 Функция
энергии, доказывающая устойчивость подобных систем, сконструирована,
но она не рассматривается здесь из-за своего концептуального сходства с
дискретным случаем.
Функция
энергии, доказывающая устойчивость подобных систем, сконструирована,
но она не рассматривается здесь из-за своего концептуального сходства с
дискретным случаем.
Если  велико, непрерывные системы функционируют
подобно дискретным бинарным системам, окончательно стабилизируясь со
всеми выходами, близкими нулю или единице, т. е. в вершине единичного
гиперкуба. С уменьшением
велико, непрерывные системы функционируют
подобно дискретным бинарным системам, окончательно стабилизируясь со
всеми выходами, близкими нулю или единице, т. е. в вершине единичного
гиперкуба. С уменьшением  устойчивые точки удаляются от
вершин, последовательно исчезая по мере приближения
устойчивые точки удаляются от
вершин, последовательно исчезая по мере приближения  к
нулю.
На рис. 9.1 показаны линии энергетических уровней непрерывной
системы с двумя нейронами.
к
нулю.
На рис. 9.1 показаны линии энергетических уровней непрерывной
системы с двумя нейронами.


