НОУ ИНТУИТ | Основы теории вычислимых функций. Лекция 8: Арифметическая иерархия

Учитесь и получайте официальные документы БЕСПЛАТНО. Вы можете поддержать наш проект.

Регистрация Вход

Твой путь к знаниям!

Опубликован: 16.03.2007 | Уровень: профессионал | Доступ: платный

|

Вам нравится? Нравится 5 студентам

| Поделиться |

Поддержать программу

Классификация множеств в иерархии

Интересно посмотреть, какое место разные конкретные множества занимают в описанной нами иерархии. Например, что можно сказать о множестве номеров какой-то фиксированной вычислимой функции в главной нумерации?

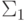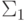Мы уже говорили, что множество всех номеров всех функций с непустой областью определения перечислимо, то есть принадлежит классу $\Sigma _{1}$ . Следовательно, его дополнение, множество всех номеров нигде не определенной функции, принадлежит классу $\Pi _{1}$ . (Классу $\Sigma _{1}$ оно принадлежать не может, так как неразрешимо, см. теорему 21)

70.Докажите, что множество номеров нигде не определенной функции в любой главной нумерации является m -полным в классе $\Pi _{1}$ множеством.

А что можно сказать о номерах других функций? Например, что можно сказать о множестве номеров тождественно нулевой функции? Оказывается, можно получить в некотором смысле полный ответ на этот вопрос.

Теорема 59. (а) Пусть U вычислимая универсальная функция для класса вычислимых функций. Тогда множество тех n, при которых U_n всюду определено и тождественно равно 0, принадлежит классу $\Pi _{2}$ . (б) Пусть U главная универсальная функция. Тогда указанное множество является m -полным в классе $\Pi _{2}$ .

Заметим, что требование главности в пункте (б) существенно: в однозначной нумерации это множество состоит из единственного номера.

Интересующее нас свойство числа n можно записать так: для любого k найдется такое t, что за t шагов вычисление значения U(n,k) закончится и даст результат 0. Выделенная часть является разрешимым свойством, а перед ней стоят два квантора как раз нужного вида. Итак, пункт (а) доказан.

Докажем утверждение (б). Пусть имеется произвольное множество P из класса $\Pi _{2}$ . При этом

$x \in P \Leftrightarrow \forall\ y\ \exists\ z\ R(x,y,z),$

где R некоторое разрешимое свойство. Рассмотрим теперь функцию S(x,y), вычисляемую таким алгоритмом: перебирая все числа, ищем число z, для которого R(x,y,z) ; как только (и если) такое число найдено, выдаем на выход 0. Ясно, что x -ое сечение S_x функции S будет тождественно нулевой функцией в том и только том случае, когда $x\in P$ . Применим свойство главности и получим функцию s, для которой U_s(x)=S_x. Она и будет сводить P к множеству всех номеров тождественно нулевой функции.

Что можно сказать про другие функции? Для любой вычислимой универсальной функции U и любой вычислимой функции f множество всех U -номеров функции f является $\Pi _{2}$ -множеством. Верен даже более сильный факт: свойство U_m=U_n (числа m и n являются номерами одной и той же функции) является $\Pi _{2}$ -свойством пары $\langle m,n\rangle$ , поэтому тем более любое его сечение (е множество всех номеров любой конкретной функции) является $\Pi _{2}$ -множеством.В самом деле, свойство U_m=U_n можно сформулировать так: " для всяких x и t₁ найдется такое t₂, что если вычисление U(m,x) завершается за t₁ шагов, то вычисление U(n,x) завершается за t₂ шагов с тем же результатом, и наоборот ". Выделенная часть разрешима, а до нее стоит $\Pi _{2}$ -префикс.

Можно даже понять, для каких функций множество номеров является $\Pi _{2}$ -полным: для функций с бесконечной областью определения. Если область определения функции конечна, то множество всех ее номеров является 0' -разрешимым (и потому не $\Pi _{2}$ -полным): имея оракул для проблемы остановки, можно убедиться, что функция определена всюду, где она должна быть определена (после чего проверить, что значения правильны), а затем проверить, что ни в одной из оставшихся точек она не определена (процесс поиска точки вне данного конечного множества, в которой функция определена, является перечислимым процессом и потому его успешность может быть проверена с помощью 0' -оракула).

Если же функция имеет бесконечную область определения, то существует бесконечное разрешимое множество, во всех точках которого функция определена (задача 12). Затем можно использовать по существу ту же конструкцию, что и для нулевой функции, но только внутри этого подмножества (не трогая элементов вне него).

71.Проведите это рассуждение подробно.

72.Покажите, что множество всех номеров всех всюду определенных функций (в главной нумерации) является $\Pi _{2}$ -полным.

73.В каком наименьшем классе арифметической иерархии лежит множество номеров всех функций с бесконечной областью определения? Будет ли оно m -полным в этом классе?

74.Покажите, что для любой (не обязательно главной!) нумерации множество всех номеров всюду определенных функций неперечислимо. Более того, оно не имеет перечислимого подмножества, включающего в себя хотя бы по одному номеру каждой вычислимой всюду определенной функции. (Указание: используйте диагональную конструкцию.)

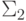В книге Х.Роджерса ([8], параграф 14.8) приведено много результатов подобного рода для многих других свойств вычислимых функций и перечислимых множеств. Например, для любого m -полного множества K множество всех его номеров является $\Pi _{2}$ -полным. (Здесь и далее, говоря о номерах, мы имеем в виду главную нумерацию перечислимых множеств.) Множество номеров всех конечных множеств является $\Sigma _{2}$ -полным. Множество номеров множеств, содержащих хотя бы один номер бесконечного множества, является $\Sigma _{3}$ -полным. Множество номеров всех разрешимых множеств является $\Sigma _{3}$ -полным. Множество номеров всех множеств с конечными дополнениями является $\Sigma _{3}$ -полным.

75. Докажите перечисленные утверждения (или прочтите их доказательства в книге Роджерса [8]).

76. Рассмотрим квантор $\exists ^\infty x$ , который читается как "существует бесконечно много x, для которых". Покажите, что все свойства из класса $\Pi _{2}$ (и только они) представимы в виде