|
Входит ли данный курс в перечень программы по переподготовки ФСТЭК? |
Измерение формы и спектра сигналов
Измерение параметров модулированных сигналов
В радиотехнических устройствах применяются амплитудная, частотная, угловая (фазовая), импульсная и комбинированные виды модуляции. В первых трех видах модуляции амплитуда, частота или фаза синусоидального сигнала изменяется по закону изменения модулирующего напряжения. При импульсной модуляции модулирующее напряжение воздействует на видеоимпульсы и изменяет их высоту, частоту следования, длительность, а также их временное положение или относительную фазу.
Синусоидальный сигнал, модулированный по амплитуде, характеризуется коэффициентом модуляции M, по частоте – девиацией частоты 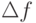 , по фазе – индексом угловой модуляции
, по фазе – индексом угловой модуляции  . Кроме того, все модулированные колебания характеризуются глубиной модуляции, равной отношению данного коэффициента, девиации или индекса модуляции к максимальному, принимаемому за 100% модуляцию.
. Кроме того, все модулированные колебания характеризуются глубиной модуляции, равной отношению данного коэффициента, девиации или индекса модуляции к максимальному, принимаемому за 100% модуляцию.
Выражение для сигнала, модулированного по амплитуде синусоидальным напряжением, имеет следующий вид:
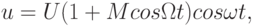 |
( 10.9) |
где U – амплитуда немодулированного высокочастотного колебания,  , f – несущая частота,
, f – несущая частота,  , F – модулирующая частота, M – коэффициент модуляции, равен отношению изменения амплитуды высокочастотного колебания при модуляции последнего к ее значению в отсутствие модуляции:
, F – модулирующая частота, M – коэффициент модуляции, равен отношению изменения амплитуды высокочастотного колебания при модуляции последнего к ее значению в отсутствие модуляции:
 |
( 10.10) |
Максимальное изменение амплитуды не должно превышать ее значения, следовательно, максимальное значение M = 1, минимальное M=0.
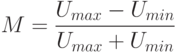 |
( 10.11) |
Формулы (10.10) и (10.11) справедливы только для симметричной модуляции. Для оценки асимметрии коэффициента модуляции измеряется раздельно "вверх" и "вниз"
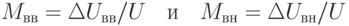 |
( 10.12) |
Коэффициент амплитудной модуляции измеряют двумя методами: осциллографическим и методом выпрямления.
Осциллографический метод осуществляют способом линейной и синусоидальной разверток. При линейной развертке в канал вертикального отклонения подают высокочастотный модулированный сигнал, а частоту развертки устанавливают в 2-3 раза ниже модулирующей частоты. На экране осциллографа появляется осциллограмма модулированного сигнала в виде 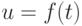 .
.
Для определения коэффициента модуляции при синусоидальной развертке в канал вертикального отклонения подают модулированный сигнал, а в канал горизонтального отклонения – модулирующее напряжение.
Метод выпрямления применяют для измерения коэффициента модуляции в процессе эксплуатации. Сущность метода заключается в том, что высокочастотный модулированный сигнал сначала детектируется, а затем измеряется стрелочными приборами постоянного и переменного тока. Приборы, основанные на этом методе, называются измерителями модуляции.
Самый распространенный способ выпрямления – способ двойного детектирования. Модулированный сигнал сначала детектируется линейным, а затем пиковым детектором. При линейном детектировании на нагрузке создается пульсирующее напряжение, постоянная составляющая которого соответствует напряжению несущей частоты U и фиксируется при помощи стрелочного индикатора. Переменная составляющая, соответствующая огибающей модулированного колебания, поступает на пиковый вольтметр с закрытым входом, показания которого в зависимости от положения переключателя П пропорциональны амплитуде 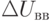 или
или  .
.
Коэффициент модуляции M определяют по формуле (10.12).
Выражение для сигнала, модулированного по частоте одним синусоидальным напряжением, имеет вид:
 |
( 10.13) |
где U – амплитуда высокочастотного колебания, 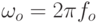 , f – значение высокой (несущей) частоты до модуляции,
, f – значение высокой (несущей) частоты до модуляции,  , F – частота модулирующего напряжения,
, F – частота модулирующего напряжения,  – индекс частотной модуляции,
– индекс частотной модуляции,
 |
( 10.14) |
где 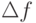 – отклонение высокой частоты при модуляции – девиация частоты.
– отклонение высокой частоты при модуляции – девиация частоты.
Девиацию частоты можно измерить несколькими методами, наиболее распространенный – метод частотного детектора. Сущность его состоит в том, что частотно-модулированные колебания преобразуются в амплитудно-модулированные, а затем детектируются амплитудным детектором, в результате чего получается напряжение, пропорциональное напряжению модулирующей частоты. Это напряжение измеряется пиковым вольтметром.
Частотно-модулированные колебания преобразуются в колебания низкой частоты частотным детектором, амплитудно-частотная характеристика которого имеет вид S-образной кривой.
Модулированный по частоте сигнал преобразуется в сигнал промежуточной частоты, усиливается до уровня, необходимого для нормальной работы ограничителя, и поступает на частотный детектор, выходное напряжение которого пропорционально девиации частоты; это напряжение проходит через фильтр нижних частот, усиливается и измеряется пиковым вольтметром. Шкала последнего проградуирована в единицах девиации – килогерцах.

