|
Раньше это можно было зделать просто нажав на тест и посмотреть результаты а сейчас никак |
Основы "живого" моделирования
15.4. Сокращение "твердого" объекта
Рассмотрим взаимодействие мышцы с тем объектом, к которому она приложена. Сокращаясь, она должна увлекать клетки объекта или только его оболочку, имитируя сокращение не только мышцы, но и всего объекта.
Пусть, как и ранее, задано значение 0 <= l <= 1 , приводящее к сокращению объекта в направлении мышцы АВ (рис. 15.3). Объект должен преобразиться, как показано на рисунке пунктиром. Мышца описывается системой параметрических уравнений (15.1). М, как и прежде, — неподвижная (относительно неподвижного объекта) точка мышцы. Однако эта точка теперь определяет плоскость М, перпендикулярную мышце, относительно которой слева и справа все значащие клетки объекта должны сместиться в направлении к этой плоскости, т.е. параллельно мышце, с коэффициентом смещения (сжатия), равным l.
Плоскость М описывается уравнением
 |
( 15.4) |
Пусть точка (xj, yj, zj) — текущая клетка объекта с адресом xjyjzj , подлежащая указанному переносу. Найдем координаты xj(M), yj(M), zj(M) ее проекции на плоскость М. Так как точка с этими координатами принадлежит плоскости М и минимизирует квадрат расстояния точки (xj, yj, zj) до этой плоскости, задача такой условной минимизации формулируется так:
найти значение xj(M), yj(M), zj(M) , удовлетворяющее требованию
(xj(M) - xj )2 + (yj(M) - yj)2 + (zj(M) - zj)2 -> min
при условии
(xj(M) - xM)(x1 - xM) + (yj(M) - yM)(y1 - yM) + (zj(M) - zM)(z1 - zM) = 0.
Решим данную задачу, используя уравнение Лагранжа
![(x_{j}^{(M)} - x_{j})^{2} + (y_{j}^{(M)} - y_{j})^{2} + (z_{j}^{(M)} - z_{j})^{2} + \lambda [(x_{j}^{(M)} - x_{M})(x_{1} - x_{M}) + (y_{j}^{(M)} - y_{M})(y_{1} - y_{M}) + (z_{j}^{(M)} - z_{M})(z_{1} - z_{M})] \to min](/sites/default/files/tex_cache/80e24a20fb20ac2d0d354eec0db25a9d.png) .
.
Дифференцируя по всем переменным, включая  и приравнивая производные нулю, получим систему линейных уравнений
и приравнивая производные нулю, получим систему линейных уравнений


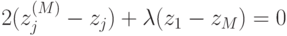
(xj(M) - xM)(x1 - xM) + (yj(M) - yM)(y1 - yM) + (zj(M) - zM)(z1 - zM) = 0.
Решая систему, находим
 |
( 15.5) |
Таким образом, получена мышца с началом в точке (клетке) с координатами xj, yj, zj и с концом в точке xj(M), yj(M), zj(M) . Эта же точка является неподвижной. Тогда по (14.2) и (14.3) имитируется сжатие мышцы. Цикл по j охватывает все значащие клетки объекта.
15.5. Сокращение вязкого тела
Вязкое тело, внутри которого сокращается мышца, характеризуется "затуханием" величины смещения клетки объекта с увеличением ее расстояния до мышцы (рис. 15.4).
Найдем квадрат r2 кратчайшего расстояния между произвольной текущей точкой объекта или только его оболочки xj, yj, zj) и мышцей. Это расстояние определяется с помощью проекции xj0, yj0, zj0) данной точки на мышцу (на рисунке — две точки, проектируемые правее А ), или ее удаленностью от концов мышцы (на рисунке — точка левее А ).
Предполагая, что данная проекция принадлежит мышце, найдем с помощью параметрического описания (15.1) соответствующее ей значение kmin из соотношения
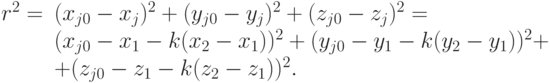 |
( 15.6) |
Значение kmin, которое определяет клетку мышцы, соответствующую искомому минимальному расстоянию, вычисляется с помощью нулевого значения производной по k:
(xj0 - x1 - k(x2 - x1)(x2 - x1) + (yj0 - y1 - k(y2 - y1)(y2 - y1) + (zj0 - z1 - k(z2 - z1)(z2 - z1) = 0
Откуда
 |
( 15.7) |
Если выполняется условие 0 <= kmin <= 1, искомая проекция действительно принадлежит мышце. Тогда r2 отыскивается в результате подстановки (15.7) в (15.6). Если kmin < 0, ближайшей точкой мышцы является А. В этом случае
r2 = (x1 - xj)2 + (y1 - yj)2 + (z1 - zj)2.
Если kmin > 1, ближайшей точкой мышцы является В:
r2 = (x2 - xj)2 + (y2 - yj)2 + (z2 - zj)2.
Чтобы определить направление переноса клетки (xj, yj, zj) , необходимо по (15.5) найти ее проекцию на плоскость М. Тогда для нахождения адресов циклической пересылки значащих клеток объекта воспользуемся формулами
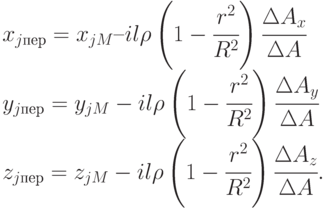 |
( 15.8) |
Здесь 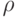 — коэффициент вязкости
и R2
— заведомо большое число,
ограничивающее значение r2
, где
смещение полностью затухает.
— коэффициент вязкости
и R2
— заведомо большое число,
ограничивающее значение r2
, где
смещение полностью затухает.
Перебор клеток объекта для пересылки выполняется по (15.3). Пересылка выполняется для обоих полупространств, разделяемых плоскостью М.



