Лекция 9: Независимые множества, клики, вершинные покрытия.

Эвристики для задачи о независимом множестве

Поиск в дереве вариантов в общем случае неэффективен, а приемы сокращения перебора, подобные описанному ниже сжатию по включению, применимы далеко не ко всем графам. Одним из выходов из этого положения является применение так называемых эвристических алгоритмов, или эвристик. Так называются алгоритмы, основанные на каких-нибудь интуитивных соображениях, которые, как кажется, ведут к получению хорошего решения. Такие алгоритмы могут иногда не давать вообще никакого решения или давать решение далеко не оптимальное. Но они, как правило, очень быстро работают и иногда (а может быть, и очень часто) дают решение, близкое к оптимальному или приемлемое для практики. Рассмотрим две простые эвристики для задачи о независимом множестве.

Одна из эвристических идей состоит в том, чтобы рассмотреть только один путь от корня до листа в дереве вариантов в надежде, что этому листу соответствует достаточно большое независимое множество. Для выбора этого единственного пути могут применяться разные соображения. В дереве вариантов, описанном выше, у каждого внутреннего узла имеются два сына. Одному из них соответствует подграф, получающийся удалением некоторой произвольно выбранной вершины , а другому - подграф, получающийся удалением окрестности этой вершины. Чтобы вместо дерева получился один путь, достаточно каждый раз выполнять какую-нибудь одну из этих двух операций. Рассмотрим оба варианта.

Допустим, мы решили каждый раз удалять выбранную вершину. Эти удаления производятся до тех пор, пока не останется граф без ребер, т.е. независимое множество. Оно и принимается в качестве решения задачи. Для полного описания алгоритма необходимо еще сформулировать правило выбора активной вершины . Мы хотим получить граф без ребер, в котором было бы как можно больше вершин. Чем меньше вершин будет удалено, тем больше их останется. Значит, цель - как можно быстрее удалить все ребра. Кажется, мы будем двигаться в нужном направлении, если на каждом шаге будем удалять наибольшее возможное на этом шаге число ребер. Это означает, что в качестве активной вершины всегда нужно выбирать вершину наибольшей степени. Алгоритмы такого типа называются жадными или градиентными. К сожалению, как будет показано дальше, оптимальный выбор на каждом шаге не гарантирует получения оптимального решения в конечном итоге.

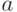Другой вариант - каждый раз удалять окрестность активной вершины . Это повторяется до тех пор, пока оставшиеся вершины не будут образовывать независимого множества. Удаление окрестности вершины равносильно тому, что сама эта вершина включается в независимое множество, которое будет получено в качестве ответа. Так как мы хотим получить в итоге как можно большее независимое множество, следует стараться удалять на каждом шаге как можно меньше вершин. Это означает, что в качестве активной вершины всегда нужно выбирать вершину наименьшей степени. Получается еще один вариант жадного алгоритма.

Имеется немало графов, для которых каждая из этих эвристик дает близкое к оптимальному, а иногда и оптимальное решение. Но, как это обычно бывает с эвристическими алгоритмами, можно найти примеры графов, для которых найденные решения будут весьма далеки от оптимальных. Рассмотрим граф , у которого множество вершин 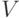состоит из трех частей мощности каждая: 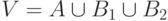, причем является независимым множеством, каждое из множеств 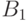, 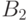- кликой, и каждая вершина из множества смежна с каждой вершиной из множества . С помощью операций суммы и соединения графов этот граф можно представить формулой . Степень каждой вершины из множества в этом графе равна , а степень каждой вершины из множеств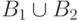а равна . Первый алгоритм, выбирающий вершину наибольшей степени, будет удалять вершины из множества до тех пор, пока не удалит их все. После этого останется граф, состоящий из двух клик, и в конечном итоге будет получено независимое множество из двух вершин. Второй алгоритм на первом шаге возьмет в качестве активной одну из вершин множества и удалит всю ее окрестность. В результате получится граф, состоящий из этой вершины и клики, а после второго шага получится независимое множество, состоящее опять из двух вершин. Итак, при применении к этому графу любой из двух эвристик получается независимое множество из двух вершин. В то же время в графе имеется независимое множество мощности .