Компьютеры и ошибки округления
Известно, что при решении задач на компьютере неизбежно возникают ошибки округления. Они крайне малы, но при решении больших задач их появляется очень много. Поэтому в совокупности они могут оказывать значительное влияние на точность получаемых результатов. Тем не менее, в курсах вычислительной математики ошибкам округления уделяется неоправданно мало внимания. Возможно, именно поэтому вокруг ошибок округления возникает немало необоснованных мнений и даже мифов.
Например, в одном из них утверждается, что при решении задач на вычислительных системах параллельной архитектуры влияние ошибок округления уменьшается и это уменьшение тем значительнее, чем больше параллелизм. В обоснование этого тезиса даже приводится вроде бы вполне разумный довод. Он сводится к тому, что на параллельных системах в каждый момент времени выполняются независимые операции. А поскольку независимые операции порождают не связанные между собой ошибки округления, то и совокупное влияние ошибок на весь вычислительный процесс становится меньше. Но как было показано в "Математически эквивалентные преобразования" , при заданном способе округления и фиксированном множестве операций ошибки округления зависят только от графа алгоритма, а совсем не от того, на какой вычислительной системе, последовательной или параллельной, реализуется сам алгоритм.
Широко распространен миф, согласно которому ошибки округления можно считать случайными величинами. Но, естественно, возникает вопрос, почему они случайные и что это означает? Имеются немало и других необоснованных постулатов. Чтобы они не становились руководством к действию, познакомимся с ошибками округления поближе.
Общий эффект от решения задачи и даже возможность ее решения во многом определяется тем, как в действительности выполняются операции над числами. А это в свою очередь зависит от принятой системы записи чисел или, как говорят, системы счисления. Наиболее совершенным принципом записи является тот, на котором основана общепринятая десятичная система. Создание вычислительной техники не связано с какими-либо принципиально другими системами счисления. Запись чисел, с которыми оперирует компьютер, основана на той же идее, что и десятичная система. В математическом плане изменения невелики и заключаются в следующем.
Зафиксируем некоторое целое положительное число р >1 и целые числа  . Пусть любое неотрицательное число x может быть
представлено в виде ряда
. Пусть любое неотрицательное число x может быть
представлено в виде ряда
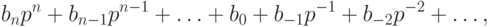
 может принимать одно из значений
может принимать одно из значений  . Перечислив подряд все коэффициенты и приписав слева знак
числа, получаем похожую на десятичную запись
. Перечислив подряд все коэффициенты и приписав слева знак
числа, получаем похожую на десятичную запись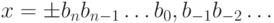
Такие формы записи чисел называются позиционными системами
счисления. Их название связано с тем, что роль, которую играет каждое
число  в записи, зависит от занимаемой им позиции. Отсчет позиции
определяется положением запятой или, что то же самое, положением
коэффициента
в записи, зависит от занимаемой им позиции. Отсчет позиции
определяется положением запятой или, что то же самое, положением
коэффициента 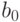 .
.
В литературе, связанной с вычислительной математикой, слово
"позиция" чаще всего заменяется словом "разряд".
Нумерация разрядов устанавливается в убывающем порядке подряд слева
направо, причем первый разряд слева от запятой имеет нулевой номер.
Различаются разряды числа до запятой и разряды после запятой. Число p
называется основанием системы счисления, числа  - базисными. Если используется система счисления с основанием p, то
правую часть представления числа x называют p -ичной дробью. Дробь
называется бесконечной, если в ее записи имеется бесконечно много
ненулевых коэффициентов, и конечной в противном случае. Обычно в
записи дроби опускаются все первые и последние нулевые коэффициенты.
Опускается и запятая, если все коэффициенты после нее являются
нулевыми.
- базисными. Если используется система счисления с основанием p, то
правую часть представления числа x называют p -ичной дробью. Дробь
называется бесконечной, если в ее записи имеется бесконечно много
ненулевых коэффициентов, и конечной в противном случае. Обычно в
записи дроби опускаются все первые и последние нулевые коэффициенты.
Опускается и запятая, если все коэффициенты после нее являются
нулевыми.
Выбор базисных чисел  определяется в основном
требованиями удобства работы с вещественными числами в данной системе
счисления. Не видно каких-либо особых преимуществ, которое дало бы
использование базисных чисел, превосходящих по модулю основание
системы счисления. Поэтому будем считать, что
определяется в основном
требованиями удобства работы с вещественными числами в данной системе
счисления. Не видно каких-либо особых преимуществ, которое дало бы
использование базисных чисел, превосходящих по модулю основание
системы счисления. Поэтому будем считать, что  для всех
для всех  . В вычислительной технике чаще всего используются системы
счисления с базисными числами
. В вычислительной технике чаще всего используются системы
счисления с базисными числами  . В дальнейшем, если не сделано
каких-либо оговорок, выполнение этого условия предполагается.
. В дальнейшем, если не сделано
каких-либо оговорок, выполнение этого условия предполагается.
Арифметические операции над числами, заданными в любой позиционной системе счисления, реализуются по таким же правилам, что и в десятичной системе. При этом используются таблицы сложения и умножения не десятичной системы, а системы с основанием p. Позиционные системы счисления широко используются для представления чисел в вычислительной технике. Наиболее часто применяется простейшая из них - двоичная система счисления. Использование именно позиционных систем объясняется возможностью реализации в них достаточно простых алгоритмов выполнения арифметических операций над числами.
Никакие технические средства не позволяют выполнять операции над
числами, заданными бесконечными дробями. Поэтому замена любого числа
конечной дробью является необходимой операцией. Округлением числа x до s разрядов в заданной системе счисления называется операция замены
этого числа таким числом 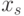 , все младшие разряды которого в той же
системе счисления, начиная с s -1-го, являются нулевыми.
Разность
, все младшие разряды которого в той же
системе счисления, начиная с s -1-го, являются нулевыми.
Разность  называется ошибкой округления.
называется ошибкой округления.
Заметим, что в данном определении ничего не говорится ни о способе выполнения операции округления, ни о том, насколько округленное число близко к округляемому. Это не случайно. В практике конструирования компьютеров операции округления реализуются самыми различными способами. Единственное, что их объединяет, - это малость в том или ином смысле ошибок округления, по крайней мере, для большинства чисел.
Один из простейших способов округления заключается в следующем.
Пусть задана p -ичная дробь 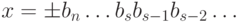 . В качестве
результата выполнения операции округления числа x до s разрядов
берется число
. В качестве
результата выполнения операции округления числа x до s разрядов
берется число 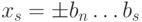 . Основное достоинство данного способа
округления - простота реализации. Однако сразу же видны и некоторые
недостатки.
. Основное достоинство данного способа
округления - простота реализации. Однако сразу же видны и некоторые
недостатки.
Предположим, что в качестве базисных берутся числа 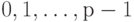 .
Тогда для ошибки округления справедливо соотношение
.
Тогда для ошибки округления справедливо соотношение  .
Равенство достигается только в одном случае, когда число
.
Равенство достигается только в одном случае, когда число  представлено бесконечной дробью и во всех его младших разрядах,
начиная с s -1-го, стоят числа p -1.
Уже сравнение с общепринятым "школьным" правилом округления в десятичной системе
показывает, что в рассмотренном способе оценка ошибки вдвое больше. Но
более важным является то, что независимо от своей величины ошибка
округления всегда имеет вполне определенный знак, противоположный
знаку округляемого числа. Это явление нежелательно, так как оно
приводит к более быстрому накоплению ошибок округления.
представлено бесконечной дробью и во всех его младших разрядах,
начиная с s -1-го, стоят числа p -1.
Уже сравнение с общепринятым "школьным" правилом округления в десятичной системе
показывает, что в рассмотренном способе оценка ошибки вдвое больше. Но
более важным является то, что независимо от своей величины ошибка
округления всегда имеет вполне определенный знак, противоположный
знаку округляемого числа. Это явление нежелательно, так как оно
приводит к более быстрому накоплению ошибок округления.
Хотя описанный способ округления чисел и не является лучшим, тем не
менее именно с ним тесно связаны все другие способы округления. В
самом деле, как бы ни выполнялась операция округления, ее результатом
будет число, все младшие разряды которого, начиная с s -1-го, являются
нулевыми. Следовательно, операцию округления всегда можно трактовать
как отбрасывание всех разрядов, начиная с s -1-го, и последующее
добавление или вычитание некоторого числа, кратного  . Для того чтобы
ошибка округления была малой, необходимо и достаточно, чтобы было
малым именно это число.
. Для того чтобы
ошибка округления была малой, необходимо и достаточно, чтобы было
малым именно это число.
Числа, имеющие нулевые младшие разряды, начиная с s -1-го, образуют
на вещественной оси равномерную сетку с шагом  . Среди этих чисел
есть число
. Среди этих чисел
есть число  , наиболее близкое к x.
Ясно, что
, наиболее близкое к x.
Ясно, что  .
Наилучшее приближение
.
Наилучшее приближение  к x будет единственным, если имеет место
строгое неравенство, и таких приближений будет два, если имеет место
равенство. Замена числа x числом
к x будет единственным, если имеет место
строгое неравенство, и таких приближений будет два, если имеет место
равенство. Замена числа x числом  является операцией округления до s разрядов, причем лучшей во многих отношениях. Однако по сравнению с
описанной ранее операцией она имеет два существенных недостатка. Во-первых,
для ее реализации необходимо всегда дополнительно осуществлять
проверку, какой из двух кандидатов должен быть взят в качестве
округленного числа
является операцией округления до s разрядов, причем лучшей во многих отношениях. Однако по сравнению с
описанной ранее операцией она имеет два существенных недостатка. Во-первых,
для ее реализации необходимо всегда дополнительно осуществлять
проверку, какой из двух кандидатов должен быть взят в качестве
округленного числа  . После этой проверки примерно в половине
случаев нужно дополнительно выполнить еще одну операцию сложения
чисел. Так как округление осуществляется после каждой арифметической
операции, реализация наилучшего по точности округления приводит к
замедлению работы арифметических устройств компьютера. Кроме этого,
есть некоторая неоднозначность в выполнении данного варианта операции
округления, когда имеется два наилучших приближения
. После этой проверки примерно в половине
случаев нужно дополнительно выполнить еще одну операцию сложения
чисел. Так как округление осуществляется после каждой арифметической
операции, реализация наилучшего по точности округления приводит к
замедлению работы арифметических устройств компьютера. Кроме этого,
есть некоторая неоднозначность в выполнении данного варианта операции
округления, когда имеется два наилучших приближения  к числу x.
Хотя такая неоднозначность встречается относительно редко, она совсем
не безобидна, как будет показано в дальнейшем.
к числу x.
Хотя такая неоднозначность встречается относительно редко, она совсем
не безобидна, как будет показано в дальнейшем.
Естественным является желание объединить достоинства обоих способов округления. Покажем, как этого можно добиться путем использования специальных систем счисления.
До сих пор предполагалось, что в качестве базисных чисел p -ичной
системы счисления используются числа  . При этом
оказалось, что лучший по точности способ округления не является самым
простым в реализации и приводит к замедлению выполнения арифметических
операций. Рассмотрим теперь p -ичные позиционные системы счисления с
другими наборами базисных чисел. Пусть основание p системы счисления
является нечетным и в качестве базисных выбраны числа
. При этом
оказалось, что лучший по точности способ округления не является самым
простым в реализации и приводит к замедлению выполнения арифметических
операций. Рассмотрим теперь p -ичные позиционные системы счисления с
другими наборами базисных чисел. Пусть основание p системы счисления
является нечетным и в качестве базисных выбраны числа  . Такая система называется сокращенной.
. Такая система называется сокращенной.
В этом случае для всех k из заданного диапазона выполняется
неравенство  . Допустим, что перед округлением до s -го
разряда округляемое число было представлено p -ичной дробью до r -го
разряда, где r - целое число и r < s.
Снова рассмотрим число
. Допустим, что перед округлением до s -го
разряда округляемое число было представлено p -ичной дробью до r -го
разряда, где r - целое число и r < s.
Снова рассмотрим число 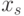 Однако теперь, принимая во внимание неравенства
Однако теперь, принимая во внимание неравенства  , получаем, что
, получаем, что
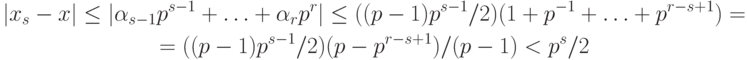
Из этих соотношений вытекает несколько интересных выводов. Главный
из них состоит в том, что в любой сокращенной системе счисления
простое отбрасывание всех младших разрядов, начиная с s -1-го, дает
правильно округленное число. В таких системах нет необходимости
задавать отдельно знак числа, так как он совпадает со знаком старшего
разряда. В любой сокращенной системе не возникает никакой
неоднозначности при правильном округлении, о чем говорилось ранее.
Можно также показать, что  , если первый из ненулевых отброшенных
разрядов отрицательный, и
, если первый из ненулевых отброшенных
разрядов отрицательный, и  , если он положительный. Число
, если он положительный. Число 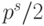 не
может быть представлено конечной дробью и т.д.
не
может быть представлено конечной дробью и т.д.
Среди сокращенных позиционных систем счисления простейшей является троичная система. Как уже отмечалось, в современной вычислительной технике наиболее широко используется двоичная система. С точки зрения округления чисел этот выбор не является лучшим. Но если троичная система счисления так хороша, то почему же нет большого числа построенных на ней компьютеров?
Рядовой пользователь не видит систему счисления, лежащую в основе работы компьютера, поскольку он отгорожен от нее языком программирования. С точки зрения пользователя троичная система хороша только тем, что позволяет без каких-либо дополнительных усилий получать более точные результаты. Безусловно, это очень важно. Однако достижение лучшей точности очень редко становится приоритетным условием для конструкторов компьютеров. Поэтому в первую очередь на выбор системы счисления влияют другие факторы. Это и трудности построения большого числа базисных элементов, имеющих 3 устойчивых состояния, и традиции конструирования элементной базы, и конкуренция в среде производителей компьютеров, и многое другое.
Тем не менее, совсем не очевидно, на каких принципах и с какой целевой функцией будут строиться компьютеры в будущем. И вполне возможно, что троичная система счисления еще окажется востребованной. Тем более что успешный опыт создания компьютера на такой системе имеется. Это машина "Сетунь". Она была разработана в вычислительном центре Московского университета в конце 50-х годов прошлого столетия. Ее главным конструктором является к.т.н. Н.П.Брусенцов, программное обеспечение выполнялось под руководством проф. Е.А.Жоголева.
Запоминание цифровой информации во всех компьютерах основано на использовании достаточно простых однотипных элементов. Каждый из таких элементов представляет некоторое физическое устройство, имеющее p устойчивых состояний, где p >1. При этом само устройство допускает возможность перевода любого своего состояния в любое другое. Эти элементы называются базисными и служат для моделирования одного числового разряда p -ичной системы счисления.
Компьютер не может содержать бесконечно много базисных элементов. Поэтому он всегда имеет возможность оперировать лишь с конечным числом конечных р -ичных дробей. Это важный вывод, из которого вытекают все основные особенности компьютерной арифметики.

