|
Здравствуйте Владимир (Ефименко). Я обучаюсь по программе повышения квалификации "Наноэлектронная элементная база информатики на основе полупроводников и ферромагнетиков". У меня проблема с тестом № 2 (к лекции № 2) по этой программе. Я несколько раз пытался пройти этот тест, но больше 50 баллов набрать не удаётся, хотя я всё делаю в соответствии сматериалом лекции. В заданиях этого теста есть ошибки, которые видны невооружённым глазом. Обращаюсь к Вам как к инспектору этой программы повышения квалификации. Найдите возможность исправить ошибки в тесте № 2. Из-за остановки на этом тесте я не могу двигаться дальше, а у меня очень ограниченное время на освоение этой программы. Заранее благодарен Вам за внимание к моим проблемам и помощь. |
Качественные изменения свойств при переходе к наноразмерным элементам
Одноэлектронное туннелирование
В лекции 1 мы рассказывали о туннельном токе между наноразмерным острием металлического зонда и электропроводящим образцом. В общем случае речь идет о том, что в квантовой механике частица описывается как волна, "облако", распределенное по всей области пространства, где ее волновая функция отлична от нуля. И есть определенная вероятность найти микрочастицу в любой точке этого пространства, даже там, куда по классическим представлениям она никак не может попасть. Поэтому в ряде случаев частица может проникать сквозь потенциальные барьеры, проходя словно сквозь "туннели" в них. В силу этого случаи такого просачивания называют "туннельным эффектом". Многочисленные эксперименты и практические применения доказали правоту в этом вопросе именно квантовой, а не классической механики.
Кулоновская блокада
В наноэлектронике туннельный эффект чаще всего используют для прохождения электронов проводимости сквозь тонкий (порядка 1-10 нм) слой изолятора между двумя проводниками ("туннельный переход",
рис.
3.6.а). Энергетическая диаграмма для этой системы такая же, как показано в лекции 1 на
рис.
1.3 справа, лишь "Вакуум" надо заменить на диэлектрик, а "Зонд" и "Образец" – на электроды Эл1 и Эл2. Как и там, "прозрачность" вакуумного барьера и туннельный электрический ток описываются выражением (1.2), т.е. зависимость их от толщины барьера, а также от работы выхода ( ) является приблизительно экспоненциальной.
) является приблизительно экспоненциальной.
а) Структура туннельного перехода. Справа – временные диаграммы: б) включения напряжения; в,г) электрического тока и напряжения на переходе, когда напряжение мало; д,е) напряжения на переходе и электрического тока, когда приложенное напряжение превышает UК. ж) Зависимость среднего тока сквозь туннельный переход от приложенного напряжения
Когда хотя бы один из электродов имеет площадь порядка единиц квадратного нанометра, тогда электрическая емкость  между электродами оказывается очень малой, и наблюдаются особые явления. Ведь для перемещения электрона из электрода Эл1 на электрод Эл2 надо выполнить работу
между электродами оказывается очень малой, и наблюдаются особые явления. Ведь для перемещения электрона из электрода Эл1 на электрод Эл2 надо выполнить работу  против сил кулоновского притяжения. Наибольшая работа, которую способен выполнить источник напряжения
против сил кулоновского притяжения. Наибольшая работа, которую способен выполнить источник напряжения  по перемещению электрического заряда
по перемещению электрического заряда  , равна
, равна 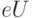 . Поэтому для того, чтобы электрон мог перейти из электрода Эл1 на электрод Эл2, должно быть выполнено условие
. Поэтому для того, чтобы электрон мог перейти из электрода Эл1 на электрод Эл2, должно быть выполнено условие
 |
( 3.19) |
Потенциал
 |
( 3.20) |
На
рис.
3.6.б показана временная диаграмма включения источника напряжения, на
рис.
3.6.в – ток 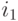 зарядки емкости
зарядки емкости  после включения напряжения, на
рис.
3.6.г – изменение напряжения
после включения напряжения, на
рис.
3.6.г – изменение напряжения  на емкости в случае, когда условие (3.19) не выполняется. В результате протекания кратковременного тока емкость
на емкости в случае, когда условие (3.19) не выполняется. В результате протекания кратковременного тока емкость  заряжается до потенциала
заряжается до потенциала  , и дальнейшее протекание тока прекращается. Это состояние называют "кулоновской блокадой" (англ. Coulomb blockade).
Она становится заметной лишь в наноэлектронике. Ведь даже при емкости туннельного перехода в 1 пФ кулоновский потенциал
, и дальнейшее протекание тока прекращается. Это состояние называют "кулоновской блокадой" (англ. Coulomb blockade).
Она становится заметной лишь в наноэлектронике. Ведь даже при емкости туннельного перехода в 1 пФ кулоновский потенциал  составляет лишь 80 нВ. А вот при емкости 10-18 Ф имеем уже
составляет лишь 80 нВ. А вот при емкости 10-18 Ф имеем уже  = 80 мВ, что легко заметить.
= 80 мВ, что легко заметить.
Важной является и температура окружающей среды. Ведь кулоновскую блокаду можно наблюдать и использовать лишь при условии, когда кулоновская энергия намного превышает энергию хаотического теплового движения электронов
 |
( 3.21) |
Одноэлектронные колебания
На
рис.
3.6.д показана временная диаграмма изменения напряжения UC2 на емкости  после включения источника напряжения в случае, когда
после включения источника напряжения в случае, когда  . Емкость начинает заряжаться, но как только напряжение на ней превышает
. Емкость начинает заряжаться, но как только напряжение на ней превышает  , происходит туннелирование одного электрона, и напряжение на емкости прыжком падает до значения
, происходит туннелирование одного электрона, и напряжение на емкости прыжком падает до значения  . Под действием источника напряжения емкость снова начинает заряжаться, но как только напряжение на ней превышает
. Под действием источника напряжения емкость снова начинает заряжаться, но как только напряжение на ней превышает  , снова происходит туннелирование одного электрона, и напряжение на емкости прыжком падает до
, снова происходит туннелирование одного электрона, и напряжение на емкости прыжком падает до  . Этот процесс повторяется все время, пока включен источник напряжения.
Соответствующие временные изменения тока
. Этот процесс повторяется все время, пока включен источник напряжения.
Соответствующие временные изменения тока  через туннельный переход показаны на
рис.
3.6.е. Туннельный переход периодически генерирует очень короткие импульсы тока. Длительность этих импульсов можно оценить из соотношения неопределенности
через туннельный переход показаны на
рис.
3.6.е. Туннельный переход периодически генерирует очень короткие импульсы тока. Длительность этих импульсов можно оценить из соотношения неопределенности
 |
( 3.22) |
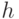 – постоянная Планка (4,14*10-15 эВ*с),
– постоянная Планка (4,14*10-15 эВ*с), 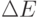 – высота туннельного барьера, в данном случае – работа выхода электрона. Если она составляет приблизительно 4 эВ, то
– высота туннельного барьера, в данном случае – работа выхода электрона. Если она составляет приблизительно 4 эВ, то 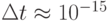 с. Периодические импульсы тока, которые сопровождают перенос каждого отдельного электрона через наноразмерный туннельный барьер, называют "одноэлектронными колебаниями". Частота этих колебаний в принципе может достигать 100 ТГц и выше. Она ограничивается лишь паразитными емкостями, электрическим сопротивлением и индуктивностями схемы.
с. Периодические импульсы тока, которые сопровождают перенос каждого отдельного электрона через наноразмерный туннельный барьер, называют "одноэлектронными колебаниями". Частота этих колебаний в принципе может достигать 100 ТГц и выше. Она ограничивается лишь паразитными емкостями, электрическим сопротивлением и индуктивностями схемы.На рис. 3.6.ж показана вольтамперная характеристика наноразмерного туннельного барьера – зависимость среднего (по времени) электрического тока от приложенного напряжения. Если материал электродов Эл1 и Эл2 одинаков, то ВАХ является симметричной.
Кулоновская лестница
Интересным оказался случай двойного туннельного барьера (
рис.
3.7.а), когда наноостровок НО из металла или полупроводника находится в диэлектрике Д между двумя электродами Эл1 и Эл2 и отделен от них тонкими туннельными барьерами. Если материалы электродов и ширина обоих барьеров приблизительно одинаковы, то ВАХ такой двойной туннельной структуры подобна ВАХ на
рис.
3.6.ж, но, как правило, немного сдвинута в ту или другую сторону вдоль горизонтали (
рис.
3.7.б). Это связано с начальным (при  ) зарядовым состоянием наноостровка.
) зарядовым состоянием наноостровка.

Рис. 3.7. а) Структура двойного туннельного барьера. б) ВАХ приблизительно одинаковых барьеров. в) ВАХ в случае существенно разных барьеров – "кулоновская лестница"
Если же туннельные барьеры с двух сторон наноостровка значительно отличаются (шириной или высотой), то наблюдается непривычная форма ВАХ, которую называют "кулоновской лестницей" (англ. Coulomb staircase). Она объясняется тем, что сквозь один из туннельных барьеров (например, левый) электроны туннелируют значительно легче. Поэтому на наноостровок из левого электрода может туннелировать второй электрон, когда первый еще не успел туннелировать из наноостровка на правый электрод.
Кулоновская потенциальная энергия наноостровка с двумя избыточными электронами равна  , где
, где  – электрическая емкость островка. Поэтому для туннелирования на островок второго электрона надо выполнить работу
– электрическая емкость островка. Поэтому для туннелирования на островок второго электрона надо выполнить работу
 |
( 3.23) |
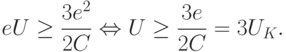 |
( 3.24) |
 |
( 3.25) |


