|
Здравствуйте Владимир (Ефименко). Я обучаюсь по программе повышения квалификации "Наноэлектронная элементная база информатики на основе полупроводников и ферромагнетиков". У меня проблема с тестом № 2 (к лекции № 2) по этой программе. Я несколько раз пытался пройти этот тест, но больше 50 баллов набрать не удаётся, хотя я всё делаю в соответствии сматериалом лекции. В заданиях этого теста есть ошибки, которые видны невооружённым глазом. Обращаюсь к Вам как к инспектору этой программы повышения квалификации. Найдите возможность исправить ошибки в тесте № 2. Из-за остановки на этом тесте я не могу двигаться дальше, а у меня очень ограниченное время на освоение этой программы. Заранее благодарен Вам за внимание к моим проблемам и помощь. |
Качественные изменения свойств при переходе к наноразмерным элементам
Изменения энергетического спектра
В случае квантовых размерных эффектов, когда размеры элементов становятся меньше длины волны де Бройля  , носители электрического заряда уже в принципе нельзя рассматривать как классические частицы, а обязательно надо учитывать их волновую природу, т.е. описывать их методами квантовой механики.
, носители электрического заряда уже в принципе нельзя рассматривать как классические частицы, а обязательно надо учитывать их волновую природу, т.е. описывать их методами квантовой механики.
Главными квантово-размерными эффектами являются:
- изменение энергетического спектра носителей электрического заряда;
- возможность их туннельного проникновения сквозь потенциальный барьер и
- явления квантовой интерференции.
Квантовая плоскость
Физическую суть изменения энергетического спектра носителей электрического заряда покажем сначала на примере идеальной "квантовой плоскости". В этом случае электрон находится в узкой (шириной  ) очень глубокой "потенциальной яме" прямоугольной формы (
рис.
3.3, слева), которая математически описывается выражением
) очень глубокой "потенциальной яме" прямоугольной формы (
рис.
3.3, слева), которая математически описывается выражением
 |
( 3.6) |
От других двух пространственных координат ( и
и 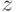 ) потенциал
) потенциал  не зависит.
не зависит.
В этом идеализированном случае решение задачи Коши для уравнения Шредингера известно и имеет вид:
 |
( 3.7) |
 |
( 3.8) |
 – постоянный множитель, который определяется из условия нормировки волновой функции.
– постоянный множитель, который определяется из условия нормировки волновой функции.
Решение существует только при целых (натуральных) значениях квантового числа  .
.
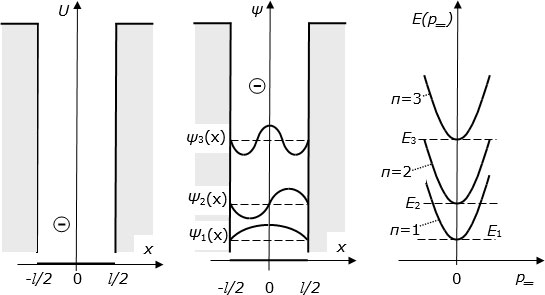
Рис. 3.3. Слева – форма потенциальной ямы. В центре – вид компонент волновой функции, зависящих от координаты х. Справа – зависимость энергии электрона проводимости от импульса p
Это означает, что  -компонента волнового вектора
-компонента волнового вектора 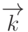 электрона и соответствующая компонента его импульса
электрона и соответствующая компонента его импульса 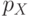 могут принимать лишь определенные значения:
могут принимать лишь определенные значения:
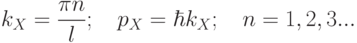 |
( 3.9) |
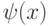 для трех первых значений квантового числа
для трех первых значений квантового числа  показаны на
рис.
3.3 в центре. На ширине
показаны на
рис.
3.3 в центре. На ширине 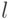 потенциальной ямы при этом укладывается точно
потенциальной ямы при этом укладывается точно  полуволн.
полуволн.Компоненты волнового вектора 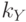 и
и  и соответствующие компоненты импульса электрона
и соответствующие компоненты импульса электрона  и
и  остаются не квантованными, т.е. могут принимать непрерывный набор значений. Кинетическая энергия электрона в потенциальной яме при разных значениях квантового числа
остаются не квантованными, т.е. могут принимать непрерывный набор значений. Кинетическая энергия электрона в потенциальной яме при разных значениях квантового числа  (в разных квантовых состояниях) равняется
(в разных квантовых состояниях) равняется
 |
( 3.10) |
 – эффективная масса электрона;
– эффективная масса электрона; 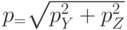 – компонента импульса электрона, параллельная квантовой плоскости;
– компонента импульса электрона, параллельная квантовой плоскости; 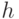 – постоянная Планка;
– постоянная Планка; 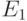 – минимальная энергия электрона в потенциальной яме. Когда электрон не движется вдоль квантовой плоскости (
– минимальная энергия электрона в потенциальной яме. Когда электрон не движется вдоль квантовой плоскости (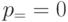 ), он имеет энергию
), он имеет энергию 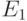 и представляет собой стоячую волну с пучностью при
и представляет собой стоячую волну с пучностью при 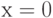 .
.Энергетический спектр электрона показан на
рис.
3.3 справа. Вдоль вертикали здесь отложена кинетическая энергия электрона, находящегося в квантовой плоскости, вдоль горизонтали – компонента 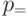 его импульса. Энергетические уровни
его импульса. Энергетические уровни 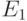 ,
,  и
и 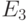 – это энергии электрона при
– это энергии электрона при 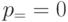 в состояниях с квантовым числом n=1,2,3. Когда электрон приходит в движение вдоль квантовой плоскости, его энергия непрерывно возрастает пропорционально
в состояниях с квантовым числом n=1,2,3. Когда электрон приходит в движение вдоль квантовой плоскости, его энергия непрерывно возрастает пропорционально 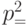 , и поэтому графики зависимости
, и поэтому графики зависимости 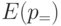 представляют собой параболы, точнее говоря, параболоиды вращения.
представляют собой параболы, точнее говоря, параболоиды вращения.
Если средняя тепловая энергия электрона проводимости (при температурах ~300 К она составляет ~0,026 эВ = 26 мэВ) меньше чем  , то при рассеяниях на неоднородностях он никак не сможет перейти из состояния
, то при рассеяниях на неоднородностях он никак не сможет перейти из состояния 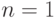 в состояние
в состояние 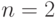 и, следовательно, не может изменить компоненту
и, следовательно, не может изменить компоненту 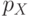 своего импульса. При рассеяниях изменяются лишь компоненты импульса
своего импульса. При рассеяниях изменяются лишь компоненты импульса  и
и  , т.е. электрон в квантовой плоскости ведет себя как двумерная частица-волна, способная двигаться лишь в пределах этой плоскости. Именно поэтому совокупность электронов проводимости внутри квантовой плоскости часто называют "двумерным электронным газом".
, т.е. электрон в квантовой плоскости ведет себя как двумерная частица-волна, способная двигаться лишь в пределах этой плоскости. Именно поэтому совокупность электронов проводимости внутри квантовой плоскости часто называют "двумерным электронным газом".
Одним из примеров реализации "квантовой плоскости" может служить гетероэпитаксиальная структура 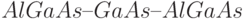 , полученная методом молекулярно-лучевой эпитаксии. Здесь тонкий слой узкозонного полупроводника
, полученная методом молекулярно-лучевой эпитаксии. Здесь тонкий слой узкозонного полупроводника 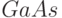 толщиной менее 30 нм находится между областями широкозонного полупроводника
толщиной менее 30 нм находится между областями широкозонного полупроводника  (
рис.
3.4).
(
рис.
3.4).
Другими примерами являются тонкий (<7 нм) канал кремниевого полевого транзистора или сверхтонкая (толщиной в несколько нанометров) металлическая пленка между слоями диэлектрика.
Конечно, в реальных гетероструктурах невозможно реализовать идеально прямоугольную потенциальную яму с бесконечно высокими стенками. А для реальных профилей потенциальных ям (на
рис.
3.4 профиль показан сплошной линией) аналитически решить квантово-механическую задачу не удается. Однако она успешно решается с помощью числовых методов на компьютерах. И общие закономерности, описанные выше для идеальной квантовой плоскости, (квантование, "двумерное поведение носителей заряда" и т.п.) в целом подтверждаются. Но имеются и важные отличия. Из-за ограниченной глубины потенциальной ямы оказывается ограниченным и число допустимых значений квантового числа  , т.е. количество дискретных энергетических уровней в "яме" (как правило, 2-5).
И, что важно, волновые функции не обращаются в нуль на границе потенциальной ямы. А это означает, что имеется определенная вероятность пребывания электрона в окрестности потенциальной ямы, т.е. там, где по классическим представлениям электрон не может находиться.
, т.е. количество дискретных энергетических уровней в "яме" (как правило, 2-5).
И, что важно, волновые функции не обращаются в нуль на границе потенциальной ямы. А это означает, что имеется определенная вероятность пребывания электрона в окрестности потенциальной ямы, т.е. там, где по классическим представлениям электрон не может находиться.


