Геометрические преобразования
Матрицы
Для выполнения преобразований векторов в пространстве мы будем
использовать матричный метод. Матрицей размерности  называется
таблица чисел вида
называется
таблица чисел вида

В дальнейшем будем использовать сокращенную запись для матрицы: 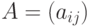 .
Строки матрицы
.
Строки матрицы  будем называть вектор-строками (поскольку каждая из
них определяет вектор), а столбцы
будем называть вектор-строками (поскольку каждая из
них определяет вектор), а столбцы  - вектор-столбцами. Матрицы
являются эффективным инструментом для выполнения преобразований на
плоскости и в пространстве. В этих случаях применяются матрицы
размерности
- вектор-столбцами. Матрицы
являются эффективным инструментом для выполнения преобразований на
плоскости и в пространстве. В этих случаях применяются матрицы
размерности  и
и  .
.
Сначала введем ряд операций над матрицами и векторами.
Пусть заданы матрицы 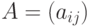 и
и 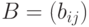 . Суммой матриц называется матрица
. Суммой матриц называется матрица  ,
элементами которой являются
,
элементами которой являются  .
.
Определим также операцию умножения матрицы на число. Результатом
умножения матрицы 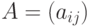 на число
на число  является матрица
является матрица 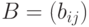 , элементы которой
, элементы которой 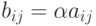 .
.
Произведением двух матриц 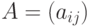 и
и 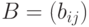 называется матрица
называется матрица  , элементы
которой определяются следующим образом:
, элементы
которой определяются следующим образом:
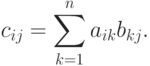
Произведение матриц некоммутативно, т.е. в общем случае  .
.
Предыдущие определения мы вводили для матриц произвольной
размерности. Следующие операции будут связаны с векторами, и мы будем
подразумевать, что 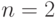 или
или 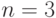 . Пусть задана матрица
. Пусть задана матрица 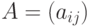 и вектор
и вектор  .
Результатом умножения матрицы на вектор является вектор
.
Результатом умножения матрицы на вектор является вектор 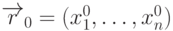 , координаты
которого вычисляются как скалярное произведение строки матрицы на
вектор:
, координаты
которого вычисляются как скалярное произведение строки матрицы на
вектор:

Если матрица 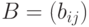 получена из матрицы
получена из матрицы 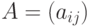 путем замены всех вектор-строк
на вектор-столбцы, т.е.
путем замены всех вектор-строк
на вектор-столбцы, т.е.  , то ее называют транспонированной матрицей
, то ее называют транспонированной матрицей  и обозначают
и обозначают  .
.
Аналогичным образом определяется умножение вектора на матрицу, только в этом случае вектор скалярно умножается на вектор-строки матрицы. Матрица вида

-
 для любой матрицы
для любой матрицы  .
. -
 для любого вектора
для любого вектора 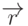 .
. - Если для матрицы
 существует матрица
существует матрица  , такая, что
, такая, что  , то
, то  называется обратной матрицей к
называется обратной матрицей к  и обозначается
и обозначается  . При этом
. При этом  , и для
любого вектора
, и для
любого вектора 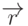 получаем соотношения: если
получаем соотношения: если  , то
, то 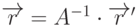 .
. - Если для матриц
 и
и  существуют обратные матрицы, то существует и
обратная матрица для их произведения и
существуют обратные матрицы, то существует и
обратная матрица для их произведения и  .
.
Благодаря операции умножения матрицы на вектор любая матрица определяет преобразование в пространстве, по которому каждому вектору сопоставляется некоторый другой по вполне определенному закону.
Отметим, что для геометрических преобразований удобно использовать матрицы размерностью на единицу больше, чем размерность пространства, но об этом подробнее речь пойдет в следующей главе.
Геометрические преобразования (перенос, масштабирование, вращение)
Геометрические объекты на плоскости и в пространстве можно подвергать ряду различных преобразований. Наиболее употребительными в задачах компьютерной графики являются:
- перемещение (параллельный перенос);
- изменение размеров (масштабирование);
- повороты вокруг некоторой точки на плоскости или некоторой оси в пространстве (вращение).
В дальнейшем мы часто будем отождествлять точки пространства с радиус-вектором, определяемым этой точкой.
Сначала рассмотрим преобразования на плоскости, или двумерные преобразования.
Параллельный перенос объекта сводится к перемещению всех его точек
на одно и то же расстояние 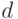 в одном и том же направлении, заданном
определенным вектором
в одном и том же направлении, заданном
определенным вектором  . Если этот вектор имеет длину
. Если этот вектор имеет длину 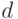 , то операция
переноса может быть реализована путем сложения всех точек объекта с
вектором
, то операция
переноса может быть реализована путем сложения всех точек объекта с
вектором  . Довольно просто доказать, что при такой операции
сохраняются расстояния между точками и, как следствие, углы между
отрезками. Понятно также, что отрезки прямых перейдут в отрезки
прямых. Поэтому при переносе многоугольника нет необходимости
подвергать этой операции бесконечное множество точек, достаточно
просто перенести вершины, а затем соединить их отрезками.
. Довольно просто доказать, что при такой операции
сохраняются расстояния между точками и, как следствие, углы между
отрезками. Понятно также, что отрезки прямых перейдут в отрезки
прямых. Поэтому при переносе многоугольника нет необходимости
подвергать этой операции бесконечное множество точек, достаточно
просто перенести вершины, а затем соединить их отрезками.
Масштабирование объекта можно реализовать путем умножения координат
всех его точек на некоторое число. Пусть имеются точки с координатами  и
и  , над которыми выполняется такое преобразование. Результатом будут
новые точки с координатами
, над которыми выполняется такое преобразование. Результатом будут
новые точки с координатами  и
и 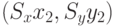 . Если
. Если  , то несложно доказать, что
обе точки переместятся вдоль прямых, проходящих через саму точку и
начало координат, т.е. в направлении своего же радиус-вектора
(рис. 3.5). При этом расстояние между новыми точками будет в
, то несложно доказать, что
обе точки переместятся вдоль прямых, проходящих через саму точку и
начало координат, т.е. в направлении своего же радиус-вектора
(рис. 3.5). При этом расстояние между новыми точками будет в 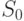 раз
отличаться от прежнего, но углы между отрезками сохранятся (это можно
показать, если выразить косинус угла через скалярное произведение
векторов). Ясно, что если коэффициент масштабирования
раз
отличаться от прежнего, но углы между отрезками сохранятся (это можно
показать, если выразить косинус угла через скалярное произведение
векторов). Ясно, что если коэффициент масштабирования 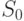 больше
единицы, соответствующий отрезок растягивается, а если меньше, то
сжимается. Кроме того, при таком преобразовании объект смещается.
больше
единицы, соответствующий отрезок растягивается, а если меньше, то
сжимается. Кроме того, при таком преобразовании объект смещается.
В случае, когда  , расстояния между точками изменятся неравномерно,
поскольку растяжения в горизонтальном и вертикальном направлениях
будут различными. Углы между отрезками также не сохранятся (рис. 3.6).
, расстояния между точками изменятся неравномерно,
поскольку растяжения в горизонтальном и вертикальном направлениях
будут различными. Углы между отрезками также не сохранятся (рис. 3.6).