НОУ ИНТУИТ | Управление ключами шифрования и безопасность сети. Лекция 17: Q. Некоторые доказательства

Учитесь и получайте официальные документы БЕСПЛАТНО. Вы можете поддержать наш проект.

Регистрация Вход

Твой путь к знаниям!

Опубликован: 19.01.2010 | Уровень: специалист | Доступ: платный

|

Вам нравится? Нравится 20 студентам

| Поделиться |

Поддержать программу

Q.2. Лекция 9

В этом разделе приводятся некоторые доказательства теорем, используемых в "лекции 1" . Мы не будем приводить длинных доказательств, таких как доказательство китайской теоремы об остатках, - интересующимся студентам рекомендуем посмотреть книги по теории чисел.

Простые числа

Мы докажем только одну теорему о простых числах.

Теорема Q.I2.Если n - составной объект, то есть простой делитель p, такой, что $p \le \surd n$ .

Доказательство:

Поскольку n - составной объект, n =a x b.

Если p - наименьший простой делитель n, тогда p <= a и p <= b.

Поэтому p²<= a x b или 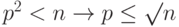$p^{2} < n \to p \le \surd n$

Эта теорема используется в решете Эратосфена, чтобы найти все простые сомножители n.

Phi-функция Эйлера

Ниже приводятся три доказательства, связанные с phi-функцией Эйлера.

Теорема Q.I3.Если p - простое число, тогда $\varphi (p)= p - 1$ .

Доказательство:

Поскольку p - простое число, все целые числа, меньшие, чем p, взаимно простые по отношению к p.

Поэтому $\varphi (p)= p - 1$ .

Эта теорема - часть phi-функции Эйлера.

Теорема Q.14.Если p - простое число и e - положительное целое число, тогда 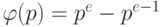$\varphi (p) =p^{e }- p^{e-1}$

Доказательство:

Целые числа, которые не являются взаимно простыми с p^e - (1 x p ), (2 x p). .., ( p^e-1 x p). Все они целые числа и имеют общий делитель p с p^e. Общее количество этих целых чисел - p^e-1. Остальная часть целых чисел является взаимно простой с p^e.

Поэтому 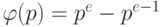$\varphi (p) =p^{e }- p^{e-1}$

Теорема Q.15.Если n - составной объект с разложением на простые множители Пp^ei, то 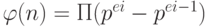$\varphi (n) = П(p^{ei} - p^{ei-1})$

Доказательство:

Доказательство базируется на факте, что 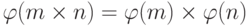$\varphi (m \times n) = \varphi (m) \times \varphi ( n)$ - мультипликативная функция, в которой m и n являются взаимно простыми. Поскольку элементы в разложении n на простые множители взаимно простые, $\varphi (Пp_{i}^{ei}) = П\varphi (p_{i}^{ei})$ .

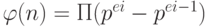
Поэтому $\varphi (n) = П(p^{ei} - p^{ei-1})$

Эта теорема - обобщение phi-функции Эйлера.

Малая теорема Ферма

Ниже приводятся две теоремы, которые относятся к малой теореме Ферма.

Теорема Q.I6.Если p - простое число и a - положительное целое число, взаимно простое c p, то $a^{p-1} \equiv 1 (mod\ p)$ .

Эта теорема - первая версия Малой теоремы Ферма.

Доказательство:

Может быть доказано, что вычеты элементов a, 2a, .., (p -1) a по модулю p равны 1,2..., (p - 1), но не обязательно в том же самом порядке,

В результате a x 2a x o o o (p - l) равно [(p - 1)]! a^p-1

В результате 1 x 2 x o - o x (p - 1) равно [(p - 1)]!

Это означает $[(p-1)]! a^{p-1}\equiv [(p - l)]! (mod\ p)$ ,

Сокразая обе стороны тождества на (p - 1)!, мы получаем 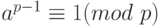$a^{p-1} \equiv 1(mod\ p)$ .

Теорема Q.I7.Если p - простое число и а - положительное целое число, то $a^{p} \equiv a (mod\ p)$ .

Эта теорема - вторая версия теоремы Ферма.

Доказательство:

Если a и p взаимно-простые, используя результат предыдущей теоремы, мы умножаем обе стороны сравнения, чтобы получить $a^{p} \equiv a (mod\ p)$ .

Если p|a, то $a^{p }\equiv a \equiv 0 (mod\ p)$ .

Теорема Эйлера

Ниже приводится доказательство одной теоремы, связанной с первой версией теоремы Эйлера. Вторую версию мы доказали в "лекции 1" .

Теорема Q.18.Если n и a являются взаимно-простыми, то $a \varphi (n) \equiv 1 (mod\ n)$ .

Доказательство:

Предположим, что элементы в $Z n* - r_{1}, r _{2,}.., r_{\varphi (n)}$

Мы создаем другой набор 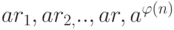$ar_{1}, ar _{2,}.., ar, a^{\varphi (n)}$ умножая каждый элемент в Z n * на a. Может быть доказано, что каждый элемент в этом новом наборе является конгруэнтным элементу в Zn* (не обязательно в том же самом порядке).

Таким образом, $ar_{1}, ar _{2,}.., ar, ar^{\varphi (n)} \equiv r_{1}, r _{2,}.., r^{\varphi (n)} (mod\ n)$

Мы имеем $a^{\varphi (n)} [r_{1} x r _{2,} x.. x r_{\varphi (n)}] \equiv r_{1} x r _{2,} x\dots x r_{\varphi (n)}] (mod\ n)$

Откуда $a^{\varphi (n)]} \equiv 1 (mod\ n)$ .

Основная теорема арифметики

Ниже приводится частичное доказательство основной теоремы арифметики.

Теорема Q.19

Основная теорема Арифметики

Ниже приводится частичное доказательство Основной теоремы Арифметики.

Теорема Q.19

Любое положительное целое число n больше чем 1 может быть представлено, как произведение простых чисел.

Доказательство:

Мы используем индукцию. Первое утверждение (база индукции) n = 2, является простым числом. Предположим, что все положительные целые числа меньше, чем n может быть представлены как произведение простых чисел. Мы докажем, что n может также быть представлено как произведение простых чисел.

Может иметь два случая: n - простое число, или n - составной объект.

Если n является простым, оно может быть представлено как произведение из одного этого простого числа,
Если n - составной объект, то мы можем написать n = a x b. Поскольку a и b - оба меньше чем n, каждое из них может быть представлено как произведение простых чисел согласно нашему предположению. Поэтому, n может быть представлено как произведение простых чисел.

Эта теорема - частичное доказательство основной теоремы арифметики. Чтобы полностью доказать эту теорему, мы должны показать, что это произведение уникально. Но мы рекомендуем посмотреть полное доказательство в книгах по теории чисел.

Дальше >>

Сетевые технологии

Управление ключами шифрования и безопасность сети