НОУ ИНТУИТ | Алгебра матриц и линейные пространства. Лекция 7: Единственность главного ступенчатого вида матрицы

Учитесь и получайте официальные документы БЕСПЛАТНО. Вы можете поддержать наш проект.

Твой путь к знаниям!

Московский государственный университет имени М.В.Ломоносова

Опубликован: 10.09.2007 | Доступ: свободный | Студентов: 3992 / 731 | Оценка: 4.33 / 3.93 | Длительность: 13:22:00

Тема: Математика

Специальности: Математик

Теги: beta, TE, алгебраическим дополнением, вычисления, геометрия, законы дистрибутивности, игры, линейная оболочка строк, матрица перехода, моноид, определитель матрицы, расширенная матрица, система линейных уравнений определенная, собственный вектор, теория, элементы

|

Вам нравится? Нравится 63 студентам

| Поделиться |

Поддержать курс

| Скачать электронную книгу

Обратимость матрицы перехода

Если |C|=0, то |C^*|=0 и строки матрицы C^* линейно зависимы. Поэтому из
$\begin{pmatrix} v'_1\\ \vdots\\ v'_n \end{pmatrix} = C^* \begin{pmatrix} v_1\\ \vdots\\ v_n \end{pmatrix},\ \ \text{т.\ е.}\ \ \mathcal E' = C^* \mathcal E,$
следует, что v'₁,...,v'_n - линейно зависимая система в V, что приводит к противоречию с тем, что v'₁,...,v'_n - базис. Итак, мы показали, что $|C|\neq 0$ и существует обратная матрица C^-1 (тогда (C^*)^-1=(C^-1)^* ).
Другое доказательство обратимости матрицы C дает интерпретация матрицы B=C^-1 как матрицы перехода от второго базиса к первому.

Действительно, элементы v₁,...,v_n также выражаются как линейные комбинации элементов базиса {v'₁,...,v'_n} :
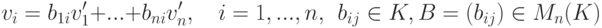
$v_i=b_{1i}v'_1+...+b_{ni}v'_n,\quad i=1,...,n,\ \ b_{ij}\in K, B=(b_{ij})\in M_n(K)$
. Тогда $\mathcal E=B^*\mathcal E'$ . Так как $\mathcal E'=C^*\mathcal E$ , то
$\mathcal E=B^*(C^*\mathcal E)=(B^*C^*)\mathcal E=(CB)^*\mathcal E.$
Так как {v₁,...,v_n} - базис в V, то (CB)^*=E, следовательно, CB=E, и поэтому B=C^-1.
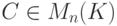Для любой обратимой матрицы $C\in M_{n}(K)$ , $|C|\neq 0$ , и любого базиса {v₁,...,v_n} конечномерного линейного пространства _K V, $\dim {}_K V=n$ , элементы $v'_1,...,v'_n\in {}_K V$ , где
$\begin{pmatrix} v'_1\\ \vdots\\ v'_n \end{pmatrix} = C^* \begin{pmatrix} v_1\\ \vdots\\ v_n \end{pmatrix},$
образуют базис линейного пространства _K V.

Действительно, в этом случае
$\begin{pmatrix} v_1\\ \vdots\\ v_n \end{pmatrix} = (C^*)^{-1} \begin{pmatrix} v'_1\\ \vdots\\ v'_n \end{pmatrix},\quad (C^*)^{-1} = (C^{-1})^*,$
т. е. n линейно независимых элементов v₁,...,v_n линейно выражаются через v'₁,...,v'_n. По основной лемме о линейной зависимости элементы v'₁,...,v'_n линейно независимы. Так как $\dim {}_K V=n$ , то {v'₁,...,v'_n} - базис линейного пространства _K V.

Замена координат элемента линейного пространства при замене базиса

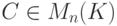Пусть {v₁,...,v_n}, {v'₁,...,v'_n} - два базиса линейного пространства _K V, $\dim {}_K V=n$ , $C\in M_{n}(K)$ , $|C|\neq 0$ , - матрица перехода от первого базиса ко второму,

$\begin{pmatrix} v'_1\\ \vdots\\ v'_n \end{pmatrix} = C^* \begin{pmatrix} v_1\\ \vdots\\ v_n \end{pmatrix},$

$x=x_1v_1+...+x_nv_n = x'_1v'_1+...+x'_nv'_n\in {}_K V$ .Так как

$\begin{mult} x = x_1v_1+...+x_nv_n = (x_1,...,x_n) \begin{pmatrix} v_1\\ \vdots\\ v_n \end{pmatrix} = {}\\ {}= (x_1,...,x_n)(C^{-1})^* \begin{pmatrix} v'_1\\ \vdots\\ v'_n \end{pmatrix} = (x'_1,...,x'_n) \begin{pmatrix} v'_1\\ \vdots\\ v'_n \end{pmatrix}, \end{mult}$

то (x'₁,...,x'_n) = (x₁,...,x_n) (C^-1)^*, или

$\begin{pmatrix} x'_1\\ \vdots\\ x'_n \end{pmatrix} = C^{-1} \begin{pmatrix} x_1\\ \vdots\\ x_n \end{pmatrix},$

что эквивалентно

$\begin{pmatrix} x_1\\ \vdots\\ x_n \end{pmatrix} = C \begin{pmatrix} x'_1\\ \vdots\\ x'_n \end{pmatrix}.$

Пример 9.9.1. Пусть V= R³, v₁=(2,1,-3), v₂=(3,2,-5), v₃=(1,-1,1). Необходимо выяснить, образуют ли элементы v₁, v₂, v₃ базис в R³, и если да, то найти координаты строки x=(6,2,-7) в базисе {v₁,v₂,v₃}.

Решение

$\begin{pmatrix} v_1\\ v_2\\ v_3 \end{pmatrix} = C^* \begin{pmatrix} e_1\\ e_2\\ e_3 \end{pmatrix},$

где {e₁,e₂,e₃} - стандартный базис в R³,

$C= \begin{pmatrix} \phm 2 & \phm 3 & \phm 1\\ \phm 1 & \phm 2 & -1\\ -3 & -5 & \phm 1 \end{pmatrix}.$

Строки v₁, v₂, v₃ образуют базис в R³ тогда и только тогда, когда матрица C обратима. Если матрица C обратима, то столбец координат строки x в базисе {v₁,v₂,v₃} равен

$C^{-1} \begin{pmatrix} \phm 6\\ \phm 2\\ -7 \end{pmatrix}.$

Для вычисления этого столбца применим алгоритм вычисления матрицы A^-1B в процессе работы которого проверяется, обратима ли матрица A=C :

$\begin{align*} & \left( \begin{array}{ccc|c} \phm 2 & \phm 3 & \phm 1 & \phm 6\\ \phm 1 & \phm 2 & -1 & \phm 2\\ -3 & -5 & \phm 1 & -7 \end{array} \right) \to \left( \begin{array}{ccc|c} \phm 1 & \phm 2 & -1 & \phm 2\\ \phm 2 & \phm 3 & \phm 1 & \phm 6\\ -3 & -5 & \phm 1 & -7 \end{array} \right) \to{}\\ & \quad {}\to \left( \begin{array}{ccc|c} \phm 1 & \phm 2 & -1 & \phm 2\\ \phm 0 & -1 & \phm 3 & \phm 2\\ -3 & -5 & \phm 1 & -7 \end{array} \right) \to \left( \begin{array}{ccc|c} 1 & 2 & -1 & \phm 2\\ 0 & 1 & -3 & -2\\ 0 & 1 & -2 & -1 \end{array} \right) \to{}\\ & \quad {}\to \left( \begin{array}{ccc|c} 1 & 2 & -1 & \phm 2\\ 0 & 1 & -3 & -2\\ 0 & 0 & \phm 1 & \phm 1 \end{array} \right) \to \left( \begin{array}{ccc|c} 1 & 2 & -1 & 2\\ 0 & 1 & \phm 0 & 1\\ 0 & 0 & \phm 1 & 1 \end{array} \right) \to{}\\ & \quad {}\to \left( \begin{array}{ccc|c} 1 & 2 & 0 & 3\\ 0 & 1 & 0 & 1\\ 0 & 0 & 1 & 1 \end{array} \right) \to \left( \begin{array}{ccc|c} 1 & 0 & 0 & 1\\ 0 & 1 & 0 & 1\\ 0 & 0 & 1 & 1 \end{array} \right). \end{align*}$

Таким образом, матрица C обратима, (1,1,1) - координаты строки x в базисе {v₁,v₂,v₃}, x=v₁+v₂+v₃.

Этот же результат можно было получить, используя формулу (6,2,-7)(C^*)^-1=(1,1,1),

$\left( \begin{array}{ccc} 2 & \phm 1 & -3\\ 3 & \phm 2 & -5\\ 1 & -1 & \phm 1\\ \hline 6 & \phm 2 & -7 \end{array} \right) \to \left( \begin{array}{ccc} 1 & 0 & 0\\ 0 & 1 & 0\\ 0 & 0 & 1\\ \hline 1 & 1 & 1 \end{array} \right)$

(здесь применяем элементарные преобразования столбцов).

Дальше >>

Авторизоваться

Алгебра матриц и линейные пространства

Единственность главного ступенчатого вида матрицы

Обратимость матрицы перехода

Замена координат элемента линейного пространства при замене базиса

Вопросы и ответы