НОУ ИНТУИТ | Алгебра матриц и линейные пространства. Лекция 5: Многочлены от матриц, теорема Гамильтона-Кэли. Обратная матрица

Учитесь и получайте официальные документы БЕСПЛАТНО. Вы можете поддержать наш проект.

Твой путь к знаниям!

Московский государственный университет имени М.В.Ломоносова

Опубликован: 10.09.2007 | Доступ: свободный | Студентов: 3973 / 713 | Оценка: 4.33 / 3.93 | Длительность: 13:22:00

Тема: Математика

Специальности: Математик

Теги: beta, TE, алгебраическим дополнением, вычисления, геометрия, законы дистрибутивности, игры, линейная оболочка строк, матрица перехода, моноид, определитель матрицы, расширенная матрица, система линейных уравнений определенная, собственный вектор, теория, элементы

|

Вам нравится? Нравится 62 студентам

| Поделиться |

Поддержать курс

| Скачать электронную книгу

Нахождение обратной матрицы A

Пусть дана квадратная матрица 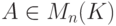$A \in M_n(K)$ такая, что $|A|\neq 0$ .

Первый способ. A^-1=B=(b_ij), $b_{ij}=\frac{A_{ji}}{|A|}$ (к сожалению, требуется вычислить n² определителей A_ji размера $(n-1)\times(n-1)$ ).

Второй способ. Найдем матрицу $X\in M_n(K)$ такую, что AX=E (тогда, по следствию 8.7.4, XA=E, X=A^-1 ). Это равносильно нахождению таких столбцов $\hat X_1,...,\hat X_n$ , что

$A\hat X_1=\hat E_1,...,\ A\hat X_n=\hat E_n,$

т. е. решению n систем линейных уравнений с матрицей A для коэффициентов и столбцами свободных членов $\hat E_1,...,\hat E_n$ (столбцы единичной матрицы). Так как $|A|\neq 0$ , то элементарными преобразованиями строк 1-го, 2-го и 3-го типов мы можем матрицу A привести к единичной матрице E. Применяя эти преобразования одновременно к n нашим системам, получаем

$(A\mid E)\mapsto...\mapsto(E\mid B).$

Но тогда столбцы матрицы B - решения наших n систем, AB=E (как мы уже отметили, в этом случае BA=E, B=A^-1 ).

Замечания 8.8.1.

Можно предложить другое обоснование этого алгоритма. Найдутся элементарные матрицы T_i 1-го, 2-го или 3-го типа такие, что 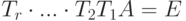$T_r\cdot...\cdot T_2T_1A=E$ , т. е. TA=E для $T=T_r\cdot...\cdot T_1$ и, следовательно, T=A^-1. Но тогда B=TE=T=A^-1.

Отсюда следует также, что группа $G=\GL_n(K)$ порождается элементарными матрицами 1-го, 2-го и 3-го типа.
Этот алгоритм можно применять и для выяснения, существует ли обратная матрица, так как если определитель |A| равен 0, то мы не сможем привести элементарными преобразованиями матрицу A к E (ступенчатый вид матрицы A будет треугольной матрицей с хотя бы одним нулем на диагонали). Это означает, что можно не вычислять определитель матрицы A перед применением алгоритма.

Пример 8.8.2.

$\begin{gathe} A= \begin{pmatrix} 1 & m\\ 0 & 1 \end{pmatrix},\quad |A|=1\neq 0,\\ \left( \begin{array}{cc|cc} 1 & m & 1 & 0\\ 0 & 1 & 0 & 1 \end{array}\right) \to \left( \begin{array}{cc|cc} 1 & 0 & 1 & -m\\ 0 & 1 & 0 & \phm 1 \end{array}\right), \end{gathe}$

т. е.

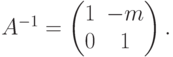
$A^{-1}= \begin{pmatrix} 1 & -m\\ 0 & \phm 1 \end{pmatrix}.$

Пример 8.8.3. Найти обратную матрицу для матрицы

$\begin{pmatrix} 5 & 2 & 0\\ 2 & 1 & 1\\ 3 & 3 & 8 \end{pmatrix},$

если она существует.

Решение

$\begin{align*} & \left( \begin{array}{ccc|ccc} 5 & 2 & 0 & 1 & 0 & 0\\ 2 & 1 & 1 & 0 & 1 & 0\\ 3 & 3 & 8 & 0 & 0 & 1 \end{array} \right) \to \left( \begin{array}{ccc|ccc} 5 & 2 & 0 & 1 & \phm 0 & 0\\ 2 & 1 & 1 & 0 & \phm 1 & 0\\ 1 & 2 & 7 & 0 & -1 & 1 \end{array} \right) \to{} \\[1mm] & \quad {}\to \left( \begin{array}{ccc|ccc} 1 & 2 & 7 & 0 & -1 & 1\\ 2 & 1 & 1 & 0 & \phm 1 & 0\\ 5 & 2 & 0 & 1 & \phm 0 & 0 \end{array} \right) \to{} %\\ %& \quad {}\to \left( \begin{array}{ccc|ccc} 1 & \phm 2 & \phm 7 & 0 & -1 & \phm 1\\ 0 & -3 & -13 & 0 & \phm 3 & -2\\ 0 & -8 & -35 & 1 & \phm 5 & -5 \end{array} \right) \to{} \\[1mm] & \quad {}\to \left( \begin{array}{ccc|ccc} 1 & \phm 2 & \phm 7 & 0 & -1 & \phm 1\\ 0 & -3 & -13 & 0 & \phm 3 & -2\\ 0 & \phm 1 & \phm 4 & 1 & -4 & \phm 1 \end{array} \right) \to{} \\[1mm] & \quad {}\to \left( \begin{array}{ccc|ccc} 1 & \phm 2 & \phm 7 & 0 & -1 & \phm 1\\ 0 & \phm 1 & \phm 4 & 1 & -4 & \phm 1\\ 0 & -3 & -13 & 0 & \phm 3 & -2 \end{array} \right) \to{} \\[1mm] & \quad {}\to \left( \begin{array}{ccc|ccc} 1 & 2 & \phm 7 & 0 & -1 & 1\\ 0 & 1 & \phm 4 & 1 & -4 & 1\\ 0 & 0 & -1 & 3 & -9 & 1 \end{array} \right) \to{} %\\ %& \quad {}\to \left( \begin{array}{ccc|ccc} 1 & 2 & 7 & \phm 0 & -1 & \phm 1\\ 0 & 1 & 4 & \phm 1 & -4 & \phm 1\\ 0 & 0 & 1 & -3 & \phm 9 & -1 \end{array} \right) \to{} \\[1mm] & \quad {}\to \left( \begin{array}{ccc|ccc} 1 & 2 & 0 & \phm 21 & -64 & \phm 8\\ 0 & 1 & 0 & \phm 13 & -40 & \phm 5\\ 0 & 0 & 1 & -3 & \phm 9 & -1 \end{array} \right) \to{} \\[1mm] & \quad {}\to \left( \begin{array}{ccc|ccc} 1 & 0 & 0 & -5 & \phm 16 & -2\\ 0 & 1 & 0 & \phm 13 & -40 & \phm 5\\ 0 & 0 & 1 & -3 & \phm 9 & -1 \end{array} \right). \end{align*}$

Итак,

$\begin{pmatrix} 5 & 2 & 0\\ 2 & 1 & 1\\ 3 & 3 & 8 \end{pmatrix}^{-1} = \begin{pmatrix} -5 & \phm 16 & -2\\ \phm 13 & -40 & \phm 5\\ -3 & \phm 9 & -1 \end{pmatrix}.$

Замечания о матричных уравнениях AX = B (случай Y A = B сводится к этому, AY = B*)

Случай 1. $A\in M_n(K)$ , $|A|\neq 0$ . Тогда существует обратная матрица A^-1, и поэтому существует единственное решение X=A^-1B уравнения AX=B (для уравнения YA=B существует единственное решение Y=BA^-1 ). При этом можно отдельно не вычислять матрицу A^-1, а применять наш алгоритм, приписывая к матрице A матрицу B, $(A\mid B)$ , и приводя элементарными преобразованиями строк к $(E\mid A^{-1}B)$ .

Пример 8.8.4. Пусть

$A= \begin{pmatrix} \phm 1 & \phm 3 & 2\\ -2 & -1 & 1\\ \phm 1 & \phm 2 & 2 \end{pmatrix},\quad B= \begin{pmatrix} \phm 8 & -16 & \phm 9\\ -6 & \phm 7 & -3\\ \phm 7 & -13 & \phm 7 \end{pmatrix}.$

Требуется найти матрицу A^{-1}B

Решение

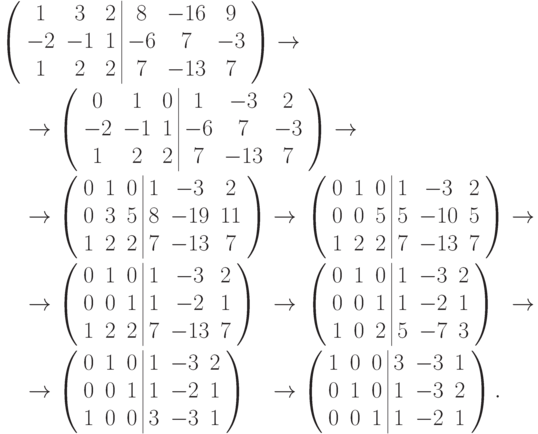
$\begin{align*} & \left( \begin{array}{ccc|ccc} \phm 1 & \phm 3 & 2 & \phm 8 & -16 & \phm 9\\ -2 & -1 & 1 & -6 & \phm 7 & -3\\ \phm 1 & \phm 2 & 2 & \phm 7 & -13 & \phm 7 \end{array} \right) \to{} \\ & \quad \begin{alignedat}{3} & {}\to \lefteqn{\left( \begin{array}{ccc|ccc} \phm 0 & \phm 1 & 0 & \phm 1 & -3 & \phm 2\\ -2 & -1 & 1 & -6 & \phm 7 & -3\\ \phm 1 & \phm 2 & 2 & \phm 7 & -13 & \phm 7 \end{array} \right) \to{}} \\ & {}\to \left( \begin{array}{ccc|ccc} 0 & 1 & 0 & 1 & -3 & 2\\ 0 & 3 & 5 & 8 & -19 & 11\\ 1 & 2 & 2 & 7 & -13 & 7 \end{array} \right) &&\to{} %\\ %& \quad {}\to \left( \begin{array}{ccc|ccc} 0 & 1 & 0 & 1 & -3 & 2\\ 0 & 0 & 5 & 5 & -10 & 5\\ 1 & 2 & 2 & 7 & -13 & 7 \end{array} \right) &&\to{} \\ & {}\to \left( \begin{array}{ccc|ccc} 0 & 1 & 0 & 1 & -3 & 2\\ 0 & 0 & 1 & 1 & -2 & 1\\ 1 & 2 & 2 & 7 & -13 & 7 \end{array} \right) &&\to{} %\\ %& \quad {}\to \left( \begin{array}{ccc|ccc} 0 & 1 & 0 & 1 & -3 & 2\\ 0 & 0 & 1 & 1 & -2 & 1\\ 1 & 0 & 2 & 5 & -7 & 3 \end{array} \right) &&\to{} \\ & {}\to \left( \begin{array}{ccc|ccc} 0 & 1 & 0 & 1 & -3 & 2\\ 0 & 0 & 1 & 1 & -2 & 1\\ 1 & 0 & 0 & 3 & -3 & 1 \end{array} \right) &&\to \left( \begin{array}{ccc|ccc} 1 & 0 & 0 & 3 & -3 & 1\\ 0 & 1 & 0 & 1 & -3 & 2\\ 0 & 0 & 1 & 1 & -2 & 1 \end{array} \right). \end{alignedat} \end{align*}$

Следовательно,

$A^{-1}B = \begin{pmatrix} 3 & -3 & 1\\ 1 & -3 & 2\\ 1 & -2 & 1 \end{pmatrix}.$

Общий случай матричного уравнения AX=B, 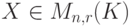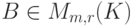$A\in M_{m,n}(K)$ , $X\in M_{n,r}(K)$ , $B\in M_{m,r}(K)$ , равносилен рассмотрению r систем линейных уравнений с матрицей A и столбцами $\hat B_1,...,\hat B_r$ в качестве столбцов свободных членов. Приведение матрицы A к ступенчатому виду A,

$(A\mid B)\mapsto (\bar A\mid \bar B),$

сводит задачу к анализу r ступенчатых систем с одной матрицей A коэффициентов и столбцами свободных членов $\Hat{\Bar{B}}_1,...,\Hat{\Bar{B}}_r$ .

Замечание 8.8.5. Вычисление матрицы Y=BA^-1 можно провести, используя элементарные преобразования столбцов:

$\left(\begin{array}{c} A\\ \hline B \end{array}\right) \to \left(\begin{array}{c} E\\ \hline BA^{-1} \end{array}\right).$

Дальше >>

Авторизоваться

Алгебра матриц и линейные пространства

Многочлены от матриц, теорема Гамильтона-Кэли. Обратная матрица

Нахождение обратной матрицы A

Замечания о матричных уравнениях AX = B (случай Y A = B сводится к этому, A*Y* = B*)

Вопросы и ответы

Замечания о матричных уравнениях AX = B (случай Y A = B сводится к этому, AY = B*)