НОУ ИНТУИТ | Алгебра матриц и линейные пространства. Лекция 2: Вычисление определителей

Учитесь и получайте официальные документы БЕСПЛАТНО. Вы можете поддержать наш проект.

Твой путь к знаниям!

Московский государственный университет имени М.В.Ломоносова

Опубликован: 10.09.2007 | Доступ: свободный | Студентов: 3991 / 731 | Оценка: 4.33 / 3.93 | Длительность: 13:22:00

Тема: Математика

Специальности: Математик

Теги: beta, TE, алгебраическим дополнением, вычисления, геометрия, законы дистрибутивности, игры, линейная оболочка строк, матрица перехода, моноид, определитель матрицы, расширенная матрица, система линейных уравнений определенная, собственный вектор, теория, элементы

|

Вам нравится? Нравится 63 студентам

| Поделиться |

Поддержать курс

| Скачать электронную книгу

Сведение вычисления определителя к определителям меньшего порядка

Определение 6.8.1 (дополняющие миноры и алгебраические дополнения). Зафиксируем элемент a_ij квадратной $(n\times n)$ -матрицы A=(a_ij). Вычеркивая в определителе |A| i -ю строку и j -й столбец (проходящие через a_ij ), получаем определитель M_ij матрицы порядка $(n-1)\times (n-1)$ , называемый дополняющим минором элемента a_ij. Алгебраическим дополнением элемента a_ij называется число A_ij=(-1)^i+jM_ij .

Замечание 6.8.2. Имеем n² (дополняющих) миноров M_ij.

Лемма 6.8.3.

$\begin{vmatrix} a_{11} & 0 & ... & 0\\ a_{21} & a_{22} & ... & a_{2n}\\ \hdotsfor{4}\\ a_{n1} & a_{n2} & ... & a_{nn} \end{vmatrix} = a_{11} \begin{vmatrix} a_{22} & ... & a_{2n}\\ \hdotsfor{3}\\ a_{n2} & ... & a_{nn} \end{vmatrix} = a_{11} M_{11} = a_{11} A_{11}.$

Доказательство. Каждый член определителя вида

$a_{11} a_{2\alpha(2)}...a_{n\alpha(n)}$

(все остальные заведомо равны нулю) входит в правую часть доказываемого равенства, при этом с тем же знаком:

$\begin{mult} \varepsilon \begin{pmatrix} 1 & 2 & ... & n\\ 1 = \alpha(1) & \alpha(2) & ... & \alpha(n) \end{pmatrix}={} \\ {}= \varepsilon \begin{pmatrix} 2 & ... & n\\ \alpha(2) & ... & \alpha(n) \end{pmatrix} = \varepsilon \begin{pmatrix} 1 & ... & n-1\\ \alpha(2)-1 & ... & \alpha(n)-1 \end{pmatrix}. \end{mult}$

Следствие 6.8.4.

$\begin{vmatrix} a_{11} & a_{12} & ... & a_{1n}\\ 0 & a_{22} & ... & a_{2n}\\ \hdotsfor{4}\\ 0 & a_{n2} & ... & a_{nn} \end{vmatrix} = a_{11} A_{11}.$

Лемма 6.8.5.

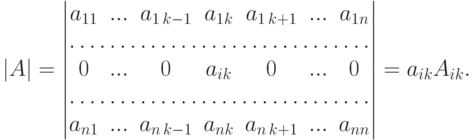
$|A| = \begin{vmatrix} a_{11} & ... & a_{1\,k-1} & a_{1k} & a_{1\,k+1} & ... & a_{1n}\\ \hdotsfor{7}\\ 0 & ... & 0 & a_{ik} & 0 & ... & 0\\ \hdotsfor{7}\\ a_{n1} & ... & a_{n\,k-1} & a_{nk} & a_{n\,k+1} & ... & a_{nn} \end{vmatrix} = a_{ik}A_{ik}.$

Доказательство. Переставляя последовательно i -ю строку (i-1) раз с (i-1) строками, стоящими над ней, а затем переставляя последовательно k -й столбец (k-1) раз с (k-1) столбцами, стоящими левее его, получаем

$\begin{mult} |A| = (-1)^{(i-1)+(k-1)} \begin{vmatrix} a_{ik} & 0 & ... & 0 & 0 & ... & 0\\ \hdotsfor{7}\\ a_{1k} & a_{11} & ... & a_{1\,k-1} & a_{1\,k+1} & ... & a_{1n}\\ \hdotsfor{7}\\ a_{nk} & a_{n1} & ... & a_{n\,k-1} & a_{n\,k+1} & ... & a_{nn} \end{vmatrix} ={} \\ {} \stackrel{\text{лемма 6.8.3}}}{= (-1)^{i+k} a_{ik} M_{ik} = a_{ik} A_{ik}. \end{mult}$

Теорема 6.8.6 (разложение определителя по i-й строке и по j-му столбцу, 1 <= i, j <= n).

$\begin{alignat*}{2} & 1) & \quad & |A|=a_{i1}A_{i1}+...+a_{in}A_{in}\ \biggl(=\sum_{j=1}^n a_{ij}A_{ij}\biggr);\\ & 2) & & |A|=a_{1j}A_{1j}+...+a_{nj}A_{nj}\ \biggl(=\sum_{i=1}^n a_{ij}A_{ij}\biggr). \end{alignat*}$

Доказательство.

Поскольку (a_i1,...,a_in)=(a_i1,0,...,0)+...+(0,...,0,a_in), то, применяя лемму 6.8.5, получаем
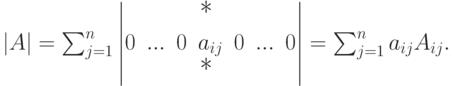
$|A|=\sum_{j=1}^n \begin{vmatrix} & & & \text{\large * }\\ 0 & ... & 0 & a_{ij} & 0 & ... & 0\\ & & & \text{\large * } \end{vmatrix} = \sum_{j=1}^{n} a_{ij}A_{ij}.$
Так как |A|=|A^*|, то разложение по j -й строке для |A^*| является разложением по j -му столбцу для |A|.

Теорема 6.8.7 (о фальшивом разложении по i-й строке и по j-му столбцу).

При $i\neq k$
$\sum_{j=1}^{n}a_{ij}A_{kj} = a_{i1}A_{k1}+...+a_{in}A_{kn}=0$
(сумма произведений элементов a_ij i -й строки на алгебраические дополнения A_kj элементов "чужой" k -й строки при $i\neq k$ равна нулю);
при $j\neq k$
$\sum_{i=1}^{n}a_{ij}A_{ik}=a_{1j}A_{1k}+...+a_{nj}A_{nk}=0$
(сумма произведений элементов a_ij j -го столбца на алгебраические дополнения A_ik элементов "чужого" k -го столбца при $j\neq k$ равна нулю).

Доказательство.

$\sum_{j=1}^{n}a_{ij}A_{kj} = \begin{vmatrix} & \text{\large * }\\ a_{i1} & ... & a_{in}\\ & \text{\large * }\\ a_{i1} & ... & a_{in}\\ & \text{\large * } \end{vmatrix} \begin{matrix} \vphantom{\text{\large * }}\\ \scriptstyle i\\ \vphantom{\text{\large * }}\\ \scriptstyle k\\ \vphantom{\text{\large * }} \end{matrix} = 0$
(разложение по k -й строке определителя, полученного из исходного заменой k -й строки на i -ю и равного 0, поскольку в нем имеется две одинаковые строки, i -я и k -я).
2) Применяя 1) к фальшивому разложению по строке для |A^*|, |A^*|=|A|, получаем фальшивое разложение по столбцу для |A|.

Пример 6.8.8. Найти определитель

$\Delta = \begin{vmatrix} 1 & 2 & 3\\ 2 & 3 & 1\\ 3 & 1 & 2 \end{vmatrix}.$

а) По определению, $\Delta = 1 \cdot 3 \cdot 2 + 2\cdot 3\cdot 1 + 2\cdot 1\cdot 3 - 3\cdot 3\cdot 3-1\cdot 1\cdot 1-2\cdot 2\cdot 2=-18$ .

б) Разлагая по первой строке, получаем

$\Delta = 1\cdot \begin{vmatrix} 3 & 1\\ 1 & 2 \end{vmatrix} + 2\cdot (-1)\cdot \begin{vmatrix} 2 & 1\\ 3 & 2 \end{vmatrix} + 3\cdot \begin{vmatrix} 2 & 3\\ 3 & 1 \end{vmatrix} =-18.$

в) Используя элементарные преобразования строк, имеем

$\begin{pmatrix} 1 & 2 & 3\\ 2 & 3 & 1\\ 3 & 1 & 2 \end{pmatrix} \to \begin{pmatrix} 1 & \phm 2 & \phm 3\\ 0 & -1 & -5\\ 3 & \phm 1 & \phm 2 \end{pmatrix} \to \begin{pmatrix} 1 & \phm 2 & \phm 3\\ 0 & -1 & -5\\ 0 & -5 & -7 \end{pmatrix} \to \begin{pmatrix} 1 & \phm 2 & \phm 3\\ 0 & -1 & -5\\ 0 & \phm 0 & \phm 18 \end{pmatrix},$

и мы пришли к треугольному виду. При этом мы применяли только преобразования 1-го типа, не меняющие определитель. Следовательно, $\Delta=-18$ .

Пример 6.8.9. Найти определитель

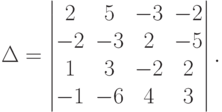
$\Delta = \begin{vmatrix} \phm 2 & \phm 5 & -3 & -2\\ -2 & -3 & \phm 2 & -5\\ \phm 1 & \phm 3 & -2 & \phm 2\\ -1 & -6 & \phm 4 & \phm 3 \end{vmatrix}.$

Используем элементарные преобразования строк, оставляя неизменной третью строку:

$\Delta\to \begin{vmatrix} \phm 0 & -1 & \phm 1 & -6\\ -2 & -3 & \phm 2 & -5\\ \phm 1 & \phm 3 & -2 & \phm 2\\ -1 & -6 & \phm 4 & \phm 3 \end{vmatrix} \to \begin{vmatrix} \phm 0 & -1 & \phm 1 & -6\\ \phm 0 & \phm 3 & -2 & -1\\ \phm 1 & \phm 3 & -2 & \phm 2\\ -1 & -6 & \phm 4 & \phm 3 \end{vmatrix} \to \begin{vmatrix} 0 & -1 & \phm 1 & -6\\ 0 & \phm 3 & -2 & -1\\ 1 & \phm 3 & -2 & \phm 2\\ 0 & -3 & \phm 2 & \phm 5 \end{vmatrix}.$

Мы применяли только преобразования 1-го типа, не меняющие определитель. Применяя разложение последнего определителя по первому столбцу, имеем

$\Delta = 1 \cdot (-1)^{3+1} \begin{vmatrix} -1 & \phm 1 & -6\\ \phm 3 & -2 & -1\\ -3 & \phm 2 & \phm 5 \end{vmatrix} = -4.$

Дальше >>

Авторизоваться

Алгебра матриц и линейные пространства

Вычисление определителей

Сведение вычисления определителя к определителям меньшего порядка

Вопросы и ответы