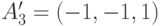Двунаправленная ассоциативная память
Кодировка ассоциаций
Обычно сеть обучается распознаванию множества образов. Обучение
производится с использованием обучающего набора, состоящего из пар
векторов  и
и 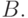 Процесс обучения реализуется в форме
вычислений; это
означает, что весовая матрица вычисляется как сумма произведений всех
векторных пар обучающего набора. B символьной форме запишем
Процесс обучения реализуется в форме
вычислений; это
означает, что весовая матрица вычисляется как сумма произведений всех
векторных пар обучающего набора. B символьной форме запишем

Предположим, что все запомненные образы представляют собой
двоичные векторы. Это ограничение будет выглядеть менее строгим, если
вспомнить, что все содержимое Библиотеки Университета может быть
закодировано в один очень длинный двоичный вектор. Показано, что более
высокая производительность достигается при использовании биполярных
векторов. При этом векторная компонента, большая чем 0, становится 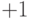 , а
компонента, меньшая или равная 0, становится
, а
компонента, меньшая или равная 0, становится 
Предположим, что требуется обучить сеть с целью запоминания трех
пар двоичных векторов, причем векторы  имеют размерность такую
же,
как и векторы
имеют размерность такую
же,
как и векторы  Надо отметить, что это не является необходимым
условием для работы алгоритма; ассоциации могут быть
сформированы и между векторами различной размерности.
Надо отметить, что это не является необходимым
условием для работы алгоритма; ассоциации могут быть
сформированы и между векторами различной размерности.
Вычисляем весовую матрицу:


Далее, прикладывая входной вектор  , вычисляем
выходной
вектор
, вычисляем
выходной
вектор  :
:

Используя пороговое правило,  , если
, если  ,
,  , если
, если  ,
,  , не изменяется, если
, не изменяется, если  ,
,
вычисляем

что является требуемой ассоциацией. Затем, подавая вектор  через обратную связь на вход первого слоя к
через обратную связь на вход первого слоя к  получаем
получаем

что дает значение  после применения пороговой функции и
образует
величину вектора
после применения пороговой функции и
образует
величину вектора 
Этот пример показывает, как входной вектор  с использованием
матрицы
с использованием
матрицы 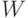 производит выходной вектор
производит выходной вектор 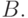 В свою
очередь, вектор
В свою
очередь, вектор  с использованием матрицы
с использованием матрицы  производит вектор
производит вектор  , и
таким образом в
системе формируется устойчивое состояние и резонанс.
, и
таким образом в
системе формируется устойчивое состояние и резонанс.
ДАП обладает способностью к
обобщению. Например, если
незавершенный или частично искаженный вектор подается в качестве  ,
сеть имеет тенденцию к выработке запомненного вектора
,
сеть имеет тенденцию к выработке запомненного вектора  , который,
в
свою очередь, стремится исправить ошибки в
, который,
в
свою очередь, стремится исправить ошибки в 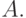 Возможно, для этого
потребуется несколько проходов, но сеть сходится к воспроизведению
ближайшего запомненного образа.
Возможно, для этого
потребуется несколько проходов, но сеть сходится к воспроизведению
ближайшего запомненного образа.
Системы с обратной связью могут иметь тенденцию к колебаниям; это означает, что они могут переходить от состояния к состоянию, никогда не достигая стабильности. Доказано, что все ДАП безусловно стабильны при любых значениях весов сети. Это важное свойство возникает из отношения транспонирования между двумя весовыми матрицами и означает, что любой набор ассоциаций может быть использован без риска возникновения нестабильности.
Существует взаимосвязь между ДАП и
рассмотренными на
предыдущих лекциях сетями Хопфилда. Если весовая матрица 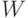 является
квадратной и симметричной, то
является
квадратной и симметричной, то  В этом случае, если слои 1 и
2
являются одним и тем же набором нейронов, ДАП превращается в
автоассоциативную сеть Хопфилда.
В этом случае, если слои 1 и
2
являются одним и тем же набором нейронов, ДАП превращается в
автоассоциативную сеть Хопфилда.