|
Зачем необходимы треугольные нормы и конормы? Как их использовать? Имеется ввиду, на практике. |
Алгоритмы нечеткого контроля и управления
В общем случае динамику дискретных систем можно представить уравнением состояния:

 — пространство состояний,
— пространство состояний,  —
множество допустимых управлений,
—
множество допустимых управлений,  —
переходная функция состояния, в общем случае нелинейная
—
переходная функция состояния, в общем случае нелинейная  .
.Эта система является детерминированной, если в любой момент времени  можно однозначно определить ее новое состояние для момента времени
можно однозначно определить ее новое состояние для момента времени  по текущему состоянию l и управлению
по текущему состоянию l и управлению 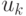 .
.
Для стохастических систем переходная функция записывается в виде
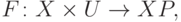
 — множество распределений вероятности на
— множество распределений вероятности на  . Для учета
неопределенностей в модель могут вводиться случайные величины или коэффициенты.
Однако для подобных моделей необходимо иметь информацию для построения
вероятностных распределений.
. Для учета
неопределенностей в модель могут вводиться случайные величины или коэффициенты.
Однако для подобных моделей необходимо иметь информацию для построения
вероятностных распределений.Не полностью определенные процессы можно моделировать с помощью аппарата нечетких множеств. Коэффициенты и некоторые величины могут быть заданы в виде функций принадлежности. Тогда динамика системы описывается нечетким отношением
![F\colon X\times U\times X\to [0,1],](/sites/default/files/tex_cache/a86c7606ae2b17e794968ab3b4fd0f28.png)
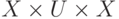 .
.Величина  рассматривается как
интенсивность перехода
или, точнее, как степень принадлежности элемента
рассматривается как
интенсивность перехода
или, точнее, как степень принадлежности элемента  образу
пары
образу
пары 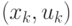 при отображении
при отображении  , т.е. основной характеристикой системы является
функция принадлежности
, т.е. основной характеристикой системы является
функция принадлежности 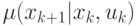 .
.
Используя понятие нечеткого отношения, можно ввести следующие пути
определения функции  :
:
1. Когда отсутствует модель процесса и имеется лишь лингвистическое описание желаемого поведения системы вида "если давление газа очень большое, то значительно увеличить расход". Подобные выражения дают информацию о том, что должно произойти в системе при поступлении на ее вход управляющих воздействий в форме нечетких множеств, определенных на универсальных множествах "давление газа" и "расход". Тогда нечеткое условное высказывание есть нечеткое отношение, которое определяется как
![F(x,u) = \min (\mu (x),\lambda (x));\quad \mu\colon X \to
[0,1];\quad \lambda\colon X \to [0,1].](/sites/default/files/tex_cache/e96c3221aa08e988f0dcf861a610a29e.png)
Если  будет являться нечеткой функцией, то состояние нечеткой
системы в момент
времени
будет являться нечеткой функцией, то состояние нечеткой
системы в момент
времени  есть условное по
есть условное по  и
и 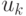 нечеткое множество,
характеризуемое функцией принадлежности
нечеткое множество,
характеризуемое функцией принадлежности  .
.
2. Возможно использование имеющейся модели системы
для задания функции  . Рассмотрим вначале случай свободной
динамики
системы и построим рекуррентную процедуру оценки состояния динамической
системы в нечетких условиях.
. Рассмотрим вначале случай свободной
динамики
системы и построим рекуррентную процедуру оценки состояния динамической
системы в нечетких условиях.
На практике ситуация усложняется частичным или полным отсутствием информации о статистических характеристиках шумов. Поэтому предлагается для решения задачи оценивания применять теорию нечетких множеств.
Рассмотрим нелинейную динамическую систему с дискретным временем:
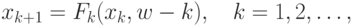
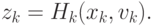
В этих уравнениях:
- индекс
 соответствует
соответствует  -му моменту времени;
-му моменту времени; -
 ,
,  — нелинейные функции соответствующих аргументов;
— нелинейные функции соответствующих аргументов; -
 — состояние динамической системы,
— состояние динамической системы, -
 — нечеткая помеха, заданная для каждого момента
времени
— нечеткая помеха, заданная для каждого момента
времени  -функцией принадлежности
-функцией принадлежности 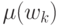 ;
; -
 — ошибка измерения с известной функцией
принадлежности
— ошибка измерения с известной функцией
принадлежности  .
.
Предполагается известной и функция принадлежности для начального
состояния  .
.
В процессе функционирования системы в общем случае носитель начального нечеткого состояния расширяется. Чтобы уменьшить неопределенность ситуаций при принятии решений, необходимо использовать дополнительную информацию о замерах и исследованиях в системе.
Будем предполагать независимость ошибок измерения, помех и состояния в
смысле
определения независимости нечетких величин. При заданной условной функции
принадлежности  состояния
состояния  и при
наличии
последовательности измерений
и при
наличии
последовательности измерений  ,
наилучшая четкая оценка состояния в момент времени
,
наилучшая четкая оценка состояния в момент времени  может быть
найдена из соотношения
может быть
найдена из соотношения

При наличии известной условной функции принадлежности  оптимальная точечная оценка состояния системы в момент
оптимальная точечная оценка состояния системы в момент  может быть
определена аналогично:
может быть
определена аналогично:

Поскольку для реальных процессов функции  и
и  являются унимодальными, то процедура
нахождения максимума довольно проста. Чтобы оценить состояния,
выведем рекуррентную процедуру для функции
принадлежности
являются унимодальными, то процедура
нахождения максимума довольно проста. Чтобы оценить состояния,
выведем рекуррентную процедуру для функции
принадлежности  . На основании
определения условной функции принадлежности можно записать, что
. На основании
определения условной функции принадлежности можно записать, что

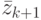 представлен в виде
представлен в виде  .
.Используя определение  и уравнение
для ошибки измерения, получаем:
и уравнение
для ошибки измерения, получаем:

Окончательно рекуррентные соотношения для нахождения апостериорной
функции принадлежности для нечеткого состояния системы на любом шаге  )
можно записать следующим образом:
)
можно записать следующим образом:

Рассмотрим теперь принципы управления нечеткой динамической системой
для функции  . Допустим, что на управляющее воздействие
. Допустим, что на управляющее воздействие 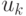 в каждый
момент времени
в каждый
момент времени  наложены нечеткие ограничения
наложены нечеткие ограничения  ,
характеризующиеся функцией принадлежности
,
характеризующиеся функцией принадлежности  , и также задано
начальное состояние
, и также задано
начальное состояние 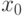 . Пусть
. Пусть  — нечеткая
цель, которую
необходимо достигнуть в момент времени
— нечеткая
цель, которую
необходимо достигнуть в момент времени  . Эта цель характеризуется
функцией принадлежности
. Эта цель характеризуется
функцией принадлежности  .
.
Оптимальные четкие управляющие воздействия 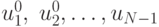 могут быть определены следующим образом:
могут быть определены следующим образом:
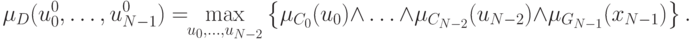
Функция 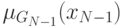 может рассматриваться как функция
принадлежности для нечеткой цели в момент времени
может рассматриваться как функция
принадлежности для нечеткой цели в момент времени  ,
индуцированной конечной целью
,
индуцированной конечной целью 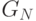 для момента
для момента  .
Зная текущее
нечеткое состояние
.
Зная текущее
нечеткое состояние  , нечеткое ограничение
, нечеткое ограничение 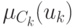 и индуцированную нечеткую цель
и индуцированную нечеткую цель  ,
на момент времени
,
на момент времени  можно найти эффективное четкое
управление
можно найти эффективное четкое
управление  .
.
