|
Зачем необходимы треугольные нормы и конормы? Как их использовать? Имеется ввиду, на практике. |
Нечеткие алгоритмы обучения
Алгоритм уточнения лингвистических критериев
Глобальные представления ЛПР о выборе альтернатив формулируются в виде
глобального критерия, и решение многокритериальной задачи сводится к построению
композиции  , где
, где
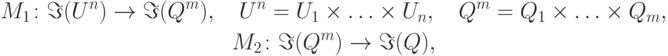
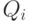 ,
,  — множества значений признаков,
локальных и глобального
критериев, соответственно.
— множества значений признаков,
локальных и глобального
критериев, соответственно. 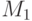 и
и  формируются
на основе высказываний
типа: "если значения признаков
формируются
на основе высказываний
типа: "если значения признаков 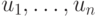 ,
характеризующие
альтернативу
,
характеризующие
альтернативу  , оцениваются термами
, оцениваются термами 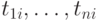 , то альтернатива
удовлетворяет
, то альтернатива
удовлетворяет  -му критерию с оценкой
-му критерию с оценкой  ".
".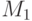 и
и  описываются наборами
описываются наборами
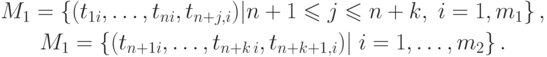
Степень удовлетворения глобальному критерию для альтернативы  вычисляется следующим образом:
вычисляется следующим образом:
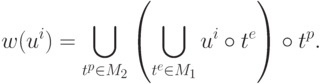
В процессе обучения уточняются оценки глобального и локальных критериев на
основе
сравнения выбранных ЛПР альтернатив  из множества
предъявленных
из множества
предъявленных 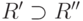 .
.  заменяется некоторым
заменяется некоторым  ,
подтверждающим соответствующий выбор:
,
подтверждающим соответствующий выбор:

Обучение осуществляется в два этапа: формирование обобщенных описаний
предпочтения ЛПР; модификация M при несовпадении предпочтений ЛПР с порядком
оценок  . На втором этапе выполняется следующее: генерация
допустимых
наборов оценок показателей; определение отношения предпочтения на парах
сгенерированных альтернатив; выделение из
. На втором этапе выполняется следующее: генерация
допустимых
наборов оценок показателей; определение отношения предпочтения на парах
сгенерированных альтернатив; выделение из  наборов,
не подлежащих корректировке; корректировка оценок по критериям.
наборов,
не подлежащих корректировке; корректировка оценок по критериям.
