|
Зачем необходимы треугольные нормы и конормы? Как их использовать? Имеется ввиду, на практике. |
Методы построения функции принадлежности. Классификация
Типы шкал
Шкалы наименований или классификации используются для описания принадлежности объектов к определенным классам. Всем объектам одного и того же класса присваивается одно и то же число, объектам разных классов — разные.
Здесь наблюдаются только два отношения: "равно" и "не равно". Следовательно, допустимы любые преобразования лишь бы одинаковые объекты были поименованы одинаковыми символами (числами, буквами, словами), а разные объекты имели бы разные имена. Этим способом фиксируются такие характеристики, как собственные имена людей, их национальность, названия населенных пунктов и т.п.
Шкала порядка применяется для измерения упорядочения объектов по единичному или совокупности признаков. Числа в шкале порядка отражают только порядок следования объектов и не дают возможности сказать, на сколько или во сколько один объект предпочтительнее другого.
Допустимыми преобразованиями для данного типа шкалы являются все монотонные преобразования, т.е. такие, которые не нарушают порядок следования значений измеряемых величин. Такие шкалы появляются, например, в результате сравнения тел по твердости. Записи "1; 2; 3" и "5,3; 12,5; 109,2" содержат одинаковую информацию о том, что первое тело самое твердое, второе менее твердое, а третье — самое мягкое. И никакой информации о том, во сколько раз одно тверже другого, на сколько единиц оно тверже и т.д., в этих записях нет, и полагаться на конкретные значения чисел, на их отношения или разности нельзя.
Разновидностью шкалы
порядка является шкала рангов, где используются
только числа, идущие подряд от 1 вверх по возрастанию.
Если среди  измеряемых объектов одинаковых нет, то ранговое
место каждого объекта в протоколе будет указано одним из целых
чисел от 1 до
измеряемых объектов одинаковых нет, то ранговое
место каждого объекта в протоколе будет указано одним из целых
чисел от 1 до  . При одинаковом значении измеряемого свойства у
. При одинаковом значении измеряемого свойства у  объектов, занимающих порядковые места с
объектов, занимающих порядковые места с  -го по
-го по  -е, их ранги будут
обозначены одинаковым числом, равным их "среднему" рангу
-е, их ранги будут
обозначены одинаковым числом, равным их "среднему" рангу  ,
где
,
где  ,
, 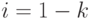 .
.
Такая разновидность шкалы порядка называется "нормированной шкалой рангов".
К типу шкал порядка относится и широко используемая шкала баллов. При этом используются целые числа в ограниченном диапозоне их значений: от 1 до 5 в системе образования, от 0 до 6 или до 10 в спорте и т.д. В любом из этих случаев протокол содержит информацию только о трех эмпирических отношениях: "<", ">" и "=".
Шкала интервалов применяется для отображения величины различия между свойствами объектов (измерение температуры по Фаренгейту и Цельсию). Шкала может иметь произвольные масштаб и точки отсчета.
Здесь между протоколами  и
и  допустимы
линейные преобразования:
допустимы
линейные преобразования:  , где
, где  — любое положительное
число, а
— любое положительное
число, а  может быть как
положительным, так и отрицательным. Это значит, что в разных протоколах
может использоваться разный масштаб единиц (a) и разные начала
отсчета (b). Примером шкал этого типа могут быть шкалы для измерения
температуры. Если в протоколе указаны градусы, но не говорится, в какой
шкале (Цельсия, Кельвина и т.д.), то во избежание недоразумений
при описании закономерностей можно использовать только отношения
интервалов,
так как при любых значениях
может быть как
положительным, так и отрицательным. Это значит, что в разных протоколах
может использоваться разный масштаб единиц (a) и разные начала
отсчета (b). Примером шкал этого типа могут быть шкалы для измерения
температуры. Если в протоколе указаны градусы, но не говорится, в какой
шкале (Цельсия, Кельвина и т.д.), то во избежание недоразумений
при описании закономерностей можно использовать только отношения
интервалов,
так как при любых значениях  и
и  сохраняется
равенство
сохраняется
равенство
![(y_{1}-y_{2}):(y_{3}-y_{4}) = [(ax_{1}+b)-(ax_{2}+b)] :
[(ax_{3}+b)-(ax_{4}+b)].](/sites/default/files/tex_cache/18a94dc5bc1930a43e37b6ea26af3a93.png)
 "),
то мы имеем
дело с протоколом в абсолютной шкале.
"),
то мы имеем
дело с протоколом в абсолютной шкале.Шкала отношений используется, например, для измерения массы, длины, веса. В этой шкале числа отражают отношения свойств объектов, т.е. во сколько раз свойство одного объекта превосходит свойство другого.
Между разными протоколами, фиксирующими один и тот же эмпирический
факт на разных языках, при этом типе шкалы должно выполняться соотношение:  , где
, где  — любое положительное число.
Один и тот же эмпирический
смысл имеют протоколы "16 кг", "16000 г", <0,016
т" и т.д.
От любой записи можно перейти к любой другой, подобрав соответствующий
множитель "
— любое положительное число.
Один и тот же эмпирический
смысл имеют протоколы "16 кг", "16000 г", <0,016
т" и т.д.
От любой записи можно перейти к любой другой, подобрав соответствующий
множитель "  ". Этот тип шкалы удобен для измерения
весов, длин и т.д.
Если нам неизвестно, в каких именно единицах записаны веса тел в разных
протоколах, то мы можем полагаться только на отношение весов двух тел:
например, тело с весом 10 единиц в два раза тяжелее тела с весом 5 единиц
вне зависимости от того, что было взято за единицу — тонна или
грамм.
Инвариантность отношений отражена в названии шкалы данного типа.
Если же в протоколе указана единица веса, то такой протокол отражает
свойства тел в абсолютной шкале.
". Этот тип шкалы удобен для измерения
весов, длин и т.д.
Если нам неизвестно, в каких именно единицах записаны веса тел в разных
протоколах, то мы можем полагаться только на отношение весов двух тел:
например, тело с весом 10 единиц в два раза тяжелее тела с весом 5 единиц
вне зависимости от того, что было взято за единицу — тонна или
грамм.
Инвариантность отношений отражена в названии шкалы данного типа.
Если же в протоколе указана единица веса, то такой протокол отражает
свойства тел в абсолютной шкале.
Шкала разностей используется для измерения свойств объектов при необходимости указания, на сколько один объект превосходит другой по одному или нескольким признакам. Является частным случаем шкалы интервалов при выборе единицы масштаба.
Абсолютная шкала — частный случай шкалы интервалов. В ней обозначается нулевая точка отсчета и единичный масштаб. Применяется для измерения количества объектов.
Допустимое преобразование для шкал данного типа представляет собой
тождество, т.е. если на одном языке в протоколе записано
"  ", а на
другом языке "
", а на
другом языке "  ", то между ними должно
выполняться простое
соотношение:
", то между ними должно
выполняться простое
соотношение: 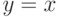 . Этот тип шкалы удобен для записи
количества
элементов в некотором конечном множестве. Если, пересчитав количество
яблок, один эксперт запишет в протоколе "6", а другой —
"VI",
то нам достаточно знать, что "6" и "VI" означают одно
и то же,
т.е., что между этими записями существует тождественное
отношение:
. Этот тип шкалы удобен для записи
количества
элементов в некотором конечном множестве. Если, пересчитав количество
яблок, один эксперт запишет в протоколе "6", а другой —
"VI",
то нам достаточно знать, что "6" и "VI" означают одно
и то же,
т.е., что между этими записями существует тождественное
отношение:  .
.
