|
Зачем необходимы треугольные нормы и конормы? Как их использовать? Имеется ввиду, на практике. |
Классы нечетких отношений
Все типы нечетких отношений в зависимости от свойств, которыми они обладают,
могут быть разделены на три больших класса. В первый класс входят
симметричные отношения, которые обычно характеризуют сходство или различие
между объектами множества  . Второй класс образуют
антисимметричные отношения;
они задают на множестве
. Второй класс образуют
антисимметричные отношения;
они задают на множестве  отношения упорядоченности,
доминирования,
подчиненности и т.п. Третий класс состоит из всех остальных отношений.
отношения упорядоченности,
доминирования,
подчиненности и т.п. Третий класс состоит из всех остальных отношений.
Отношения каждого класса, в свою очередь, могут быть разделены на подклассы в зависимости от выполнения условий рефлексивности и антирефлексивности.
Рефлексивные и
симметричные отношения обычно называют отношениями сходства,
толерантности, безразличия или неразличимости. В дальнейшем эти
отношения будем называть отношениями сходства и обозначать буквой  . Антирефлексивные и симметричные отношения
называются отношениями различия
и обозначаются буквой
. Антирефлексивные и симметричные отношения
называются отношениями различия
и обозначаются буквой  . Отношения сходства и отношения различия
двойственны друг другу. Антисимметричные отношения, называемые предпорядками и
обозначаемые буквой
. Отношения сходства и отношения различия
двойственны друг другу. Антисимметричные отношения, называемые предпорядками и
обозначаемые буквой  , в зависимости от выполнения условия рефлексивности
или антирефлексивности делятся на нестрогие и строгие порядки.
, в зависимости от выполнения условия рефлексивности
или антирефлексивности делятся на нестрогие и строгие порядки.
Из отношений третьего класса, обозначаемых буквой  , обычно
выделяют лишь рефлексивные отношения, которые будут называться слабыми порядками.
, обычно
выделяют лишь рефлексивные отношения, которые будут называться слабыми порядками.
На следующем уровне классификации из каждого класса отношений могут быть
выделены отношения специального вида. Определяющим условием для них является условие
транзитивности. Оно устанавливает связь между силой отношения для различных
пар объектов из  . Эта связь может быть очень слабой, а может
накладывать достаточно сильные ограничения на возможные значения силы отношения между
объектами из
. Эта связь может быть очень слабой, а может
накладывать достаточно сильные ограничения на возможные значения силы отношения между
объектами из  . Число отличающихся друг от друга условий
транзитивности зависит от типа отношения, для которого они формулируются.
. Число отличающихся друг от друга условий
транзитивности зависит от типа отношения, для которого они формулируются.
Условия транзитивности зависят от вида операций, с помощью которых они
определяются. Наиболее общими условиями транзитивности являются условия,
определяемые с помощью решеточных операций 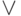 и
и 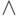 в
в  . Более частыми
являются условия, определяемые с помощью дополнительных операций в
. Более частыми
являются условия, определяемые с помощью дополнительных операций в  и зависящих от конкретного вида
и зависящих от конкретного вида  . В этих случаях указывается вид
соответствующего множества
. В этих случаях указывается вид
соответствующего множества  . Далее мы будем рассматривать нечеткие отношения,
определенные на множестве
. Далее мы будем рассматривать нечеткие отношения,
определенные на множестве ![{L=[0,1]}](/sites/default/files/tex_cache/3ea8933bdaf2cb85f0093f2910e44e5e.png) .
.
