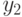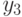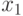|
Зачем необходимы треугольные нормы и конормы? Как их использовать? Имеется ввиду, на практике. |
Нечеткие отношения
Нечеткие отношения играют фундаментальную роль в теории нечетких систем. Аппарат теории нечетких отношений используется при построении теории нечетких автоматов, при моделировании структуры сложных систем, при анализе процессов принятия решений.
Основные определения
Теория нечетких отношений находит также приложение в задачах, в которых традиционно применяется теория обычных (четких) отношений. Как правило, аппарат теории четких отношений используется при качественном анализе взаимосвязей между объектами исследуемой системы, когда связи носят дихотомический характер и могут быть проинтерпретированы в терминах "связь присутствует", "связь отсутствует", либо когда методы количественного анализа взаимосвязей по каким-либо причинам неприменимы и взаимосвязи искусственно приводятся к дихотомическому виду. Например, когда величина связи между объектами принимает значения из ранговой шкалы, выбор порога на силу связи позволяет преобразовать связь к требуемому виду. Однако, подобный подход, позволяя проводить качественный анализ систем, приводит к потере информации о силе связей между объектами либо требует проведения вычислений при разных порогах на силу связей. Этого недостатка лишены методы анализа данных, основанные на теории нечетких отношений, которые позволяют проводить качественный анализ систем с учетом различия в силе связей между объектами системы.
Обычное неразмытое  -арное отношение
-арное отношение  определяется как подмножество
декартова произведения
определяется как подмножество
декартова произведения  множеств
множеств
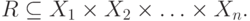
Подобно нечеткому множеству, нечеткое отношение можно задать с помощью его функции принадлежности

 — это полная
дистрибутивная решетка.
Таким образом,
— это полная
дистрибутивная решетка.
Таким образом,  — это частично упорядоченное множество, в
котором любое непустое подмножество имеет наибольшую нижнюю и наименьшую верхнюю грани и
операции пересечения и объединения в
— это частично упорядоченное множество, в
котором любое непустое подмножество имеет наибольшую нижнюю и наименьшую верхнюю грани и
операции пересечения и объединения в  удовлетворяют законам
дистрибутивности. Все операции над нечеткими
отношениями определяются с помощью этих операций из
удовлетворяют законам
дистрибутивности. Все операции над нечеткими
отношениями определяются с помощью этих операций из  .
Например, если в качестве
.
Например, если в качестве  взять ограниченное множество
вещественных чисел, то операциями пересечения и объединения в
взять ограниченное множество
вещественных чисел, то операциями пересечения и объединения в  будут,
соответственно, операции
будут,
соответственно, операции  и
и 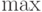 ,
и эти операции будут определять и операции над нечеткими отношениями.
,
и эти операции будут определять и операции над нечеткими отношениями.Далее мы ограничимся рассмотрением лишь бинарных нечетких отношений,
являющихся отображением на отрезок ![[0,1]](/sites/default/files/tex_cache/ccfcd347d0bf65dc77afe01a3306a96b.png) , т.е.
, т.е. ![\mu _R \colon X \times Y \to \left[ {0,1} \right]](/sites/default/files/tex_cache/f7cdf2b003cbfc6c5dc165143af93a49.png) .
.
Если множества  и
и  конечны, нечеткое отношение
конечны, нечеткое отношение  между
между  и
и  можно представить с помощью его матрицы отношения, первой строке и
первому столбцу которой ставятся в соответствие элементы множеств
можно представить с помощью его матрицы отношения, первой строке и
первому столбцу которой ставятся в соответствие элементы множеств  и
и  , а на пересечении строки
, а на пересечении строки  и столбца
и столбца  помещается элемент
помещается элемент  (см. табл.2.1).
(см. табл.2.1).
В случае, когда множества  и
и  совпадают, нечеткое отношение
совпадают, нечеткое отношение  называют нечетким
отношением на множестве X.
называют нечетким
отношением на множестве X.
В случае конечных или счетных универсальных множеств очевидна интерпретация нечеткого отношения в
виде взвешенного графа, в котором каждая пара вершин  из
из  соединяется ребром с
весом
соединяется ребром с
весом  .
.
Пример.
Пусть  и
и  , тогда
нечеткий граф, изображенный на рис рис. 2.1, задает
некоторое нечеткое отношение
, тогда
нечеткий граф, изображенный на рис рис. 2.1, задает
некоторое нечеткое отношение  .
.