Программирование задач для асинхронной ВС архитектуры "data flow"
Основы трансляции с языков высокого уровня
Общая концепция
Выбор определенной, охарактеризованной выше, структуры ПВС (ввиду смешанного характера реализованной в ней модели вычислений) ведет к необходимости решения задач наилучшего выбора входного языка системы и методов трансляции программ во внутреннее представление. В большинстве известных проектов потоковых ВС их разработчики в качестве входных языков используют специально создаваемые потоковые языки программирования, среди которых наиболее известны LAU Val Id SISAL. Все они обладают некоторыми общими свойствами, отражающими специфику потоковой обработки информации. Главное из них функциональный характер языка. Это означает, что программа состоит из функций, вырабатывающих значения, которые используются другими функциями в качестве аргументов. Функции только вырабатывают значения, следовательно, они не имеют побочных эффектов.
Другими свойствами потоковых языков являются: соблюдение правила единственного присваивания, отсутствие глобальных переменных, отказ от возможности для программиста управлять распределением памяти. Все это позволяет предельно снизить ограничения на порядок выполнения операторов-функций. Например, программа на языке LAU, ориентированная на вычислительную систему со статическим представлением программ, целиком загружается в оперативную память. Устройство управления анализирует готовность команд, используя специальные признаки, и выбирает (с помощью ассоциативного устройства) для исполнения команды, имеющие полный набор операндов. В каждый момент времени в исполнительные устройства могут быть переданы все готовые команды, вне зависимости от их последовательности в программе.
В то же время базирование указанных языков на функциональной парадигме порождает ряд проблем, не находящих простого и эффективного решения. В частности, любое (даже частичное) изменение структуры данных интерпретируется как порождение новой структуры, требующей полного дублирования исходной структуры. Понятно, что это влечет многократное увеличение нагрузки на память и коммуникационные сети.
Информационные связи, существующие в программах, препятствуют параллельному и независимому исполнению операторов. Очевидно, что свойства потоковых языков, указанные выше, служат именно устранению из программ информационных связей некоторых типов.
Например, операторы (11.2) и (11.3) во фрагменте программы
a := f1 (x1, ..., xn) (11.1)
b := f2 (y1, ..., ym, a) (11.2)
a := f3 (z1, ..., zl) (11.3)
не могут быть выполнены одновременно, поскольку оператор (11.3) меняет значение переменной a, используемой оператором (11.2). Фактически же эти операторы независимы; зависимость возникает лишь в связи с повторным использованием одного и того же имени. В потоковых языках, согласно правилу единственного присваивания, каждая переменная может быть использована в левой части оператора присваивания только один раз. Таким образом, в операторе (11.3) переменная a должна быть переименована, например, в c, и зависимость между вторым и третьим операторами исчезнет. В то же время информационная зависимость между операторами (11.1) и (11.2) устранена быть не может, и эти два оператора должны выполняться именно в указанном порядке.
Очевидно (если оставить вне рассмотрения влияние принципа единственного присваивания на всю идеологию организации вычислений в некоторых моделях потоковой обработки), что точно такой метод переименования можно формально использовать и в любом традиционном процедурном языке. Причем, чтобы не налагать ограничений на использование программистом имен переменных, это переименование может быть произведено и на этапе трансляции. Методы анализа программы при этом аналогичны методам, применяемым в оптимизирующих трансляторах. Другие свойства потоковых языков, очевидно, тоже могут быть привнесены в традиционные алгоритмические языки.
При выборе входного языка ПВС необходимо принять во внимание и следующие соображения. Любая программа на любом языке как запись выполняемого алгоритма содержит в себе всю информацию о возможности ее параллельного исполнения. Речь может идти лишь о сложности ее извлечения. Часть информации может быть извлечена при трансляции и оптимизации программы и использована для организации параллельной обработки. Количество извлеченной информации зависит при этом от выбранного алгоритма решения задачи (существуют высокопараллельные алгоритмы решения многих, традиционно полагаемых последовательными, задач), от способа представлений информации (то есть фактически от языковых средств) и от методов трансляции. Другая часть информации о возможностях параллельного выполнения программы может быть задана в явном виде. Действительно, во многих современных языках у программиста существует возможность явно указывать параллельные фрагменты программы. Следовательно, выбор языка влияет на качество распараллеливания лишь частично. Очевидно, что проще включить в существующий язык некоторые дополнительные возможности, чем разрабатывать новый язык.
Поэтому, учитывая преобладающую долю математического обеспечения в общей стоимости современных вычислительных систем, целесообразно оценить возможность использования существующих алгоритмических языков в рассматриваемой потоковой вычислительной системе.
Операторы присваивания
Определим оператор присваивания, используя общепринятую нотацию, близкую к нормальной форме Бэкуса-Наура:
<оператор присваивания> :: = <имя> := <выражение>
Имя здесь имя простой переменной (переменные с индексами для упрощения не рассматриваем). Выражения могут быть арифметическими и логическими, простыми и условными. Синтаксис их аналогичен синтаксису соответствующих конструкций языков высокого уровня:

Выражения в правой части определения, в свою очередь, могут быть условными.
Ограничитель "  " введен для упрощения
определения конца условного выражения.
При трансляции условные выражения сначала преобразуются в бесскобочное
представление, в котором все ограничители if, then, else,
" введен для упрощения
определения конца условного выражения.
При трансляции условные выражения сначала преобразуются в бесскобочное
представление, в котором все ограничители if, then, else,  сохраняют свой
порядок, а заключенные между ними арифметические и логические выражения
приобретают вид польской инверсной записи. (Отметим, что, демонстрируя составление программ
коммутации в лекции 10, мы уже фактически пользовались на уровне интуиции
теми приемами трансляции, которые теперь хотим осознать.)
сохраняют свой
порядок, а заключенные между ними арифметические и логические выражения
приобретают вид польской инверсной записи. (Отметим, что, демонстрируя составление программ
коммутации в лекции 10, мы уже фактически пользовались на уровне интуиции
теми приемами трансляции, которые теперь хотим осознать.)
Операторы присваивания преобразуются в бесскобочную запись так же, как и выражения, причем знак присваивания ":=" считаем относящимся к некоторой двуместной операции присваивания.
Рассмотрим оператор присваивания:

Его бесскобочная запись имеет вид
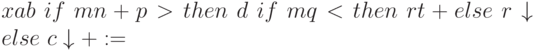 (11.4)
(11.4)
Бесскобочная запись обрабатывается транслятором за несколько проходов по следующему алгоритму.
- Взять первый элемент (FE) бесскобочной записи. NE:=FE. N:=1. Перейти к п. 3.
- Взять очередной элемент (NE). Если это последний элемент бесскобочной записи, то при N > 2 перейти к п. 1, а при N <= 2 — перейти к п. 22.
- Если NE — операнд, то перейти к п. 2.
- Если NE — знак операции, то перейти к п. 8.
- Если NE — ограничитель if, то перейти к п. 16.
- Если NE — один из ограничителей
 , то перейти к п. 2.
, то перейти к п. 2. - Ошибка неопознанный элемент.
- Если операция одноместная и имеется операнд, расположенный левее знака, то формируется команда ПВС. Если операнда нет, то перейти к п. 2. Из бесскобочной записи удаляются знак операции и операнд, а на их место подставляется математический адрес вычислителя, реализующего эту операцию. Перейти к п. 10.
- Если есть два операнда, расположенных непосредственно левее знака операции, то формируется исполнительная команда. Из бесскобочной записи удаляются знак операции и два предшествующих операнда. На их место подставляется математический адрес вычислителя-исполнителя. Если операндов нет, то перейти к п. 2.
- Взять NE . Если это последний элемент бесскобочной записи, то перейти к п. 1.
- Если NE — знак операции, то перейти к п. 10.
- Если NE — операнд, то перейти к п. 13, иначе — перейти к п. 5.
- Взять NE.
- Если NE — знак операции, то перейти к п. 13.
- Если NE — операнд, то перейти к п. 2, иначе — перейти к п. 5.
- Подготовка четырехместной команды. Три раза взять NE.
- Если три выбранных элемента образуют последовательность <операнд> <операнд> <знак>, то перейти к п. 18, иначе N := N - 3, перейти к п. 2.
- Взять NE. Если это ограничитель then, то два раза взять NE и перейти к п. 19. Иначе N := N -4, перейти к п. 2.
- Если два выбранных элемента образуют последовательность <операнд> else, то два раза взять NE. Перейти к п. 20. Иначе N := N - 2 и перейти к п. 2.
- Если два выбранных элемента образуют последовательность
 , то перейти к п. 21. Иначе N := N - 2 и перейти к п. 2.
, то перейти к п. 21. Иначе N := N - 2 и перейти к п. 2. - Формирование четырехместной команды. Изменение бесскобочной записи.
Вместо конструкции
 , где a, b, c,
d — операнды, а
, где a, b, c,
d — операнды, а  — знак
операции отношения, подставляется математический адрес вычислителя-исполнителя,
на котором формируется результат четырехместной команды. Перейти к п. 10.
— знак
операции отношения, подставляется математический адрес вычислителя-исполнителя,
на котором формируется результат четырехместной команды. Перейти к п. 10. - Выход.
В этом алгоритме N — указатель на очередной рассматриваемый элемент бесскобочной записи. Действие "Взять NE " означает перемещение указателя на следующий элемент, при этом значение N увеличивается на единицу. Изменение значения N, в свою очередь, означает перемещение указателя вправо или влево. Под элементом бесскобочной записи понимаются имена переменных, знаки операций, ограничители языка и математические адреса вычислителей. Если не указано противное, то после выполнения действий, предписанных очередным пунктом алгоритма, происходит переход на следующий по порядку пункт.
На рис. 11.7 представлена результирующая программа коммутации, получаемая при многопроходной обработке бесскобочной записи (11.4). (В командах опущены позиции индексов, поскольку они здесь не используются.)
Приведенный алгоритм трансляции формирует программу коммутации на основе
поярусного анализа графа, соответствующего оператору присваивания. При каждом
проходе транслятором бесскобочной записи формируются все команды, операнды
которых доступны в этот момент. При первом проходе формируются команда 0,
задающая сложение операндов m и n на вычислителе  , и команда 1, задающая сложение
операндов r и t на вычислителе
, и команда 1, задающая сложение
операндов r и t на вычислителе  .
.
Бесскобочная запись принимает вид
 .
.
При втором проходе не обнаруживается арифметических операций, готовых к
выполнению. Формируется пятиадресная команда 2. Она задает сравнение операндов m и q на вычислителе  . В
зависимости от результата сравнения итогом выполнения
данной команды (сформированной по ней инструкции) будет результат счета на
вычислителе
. В
зависимости от результата сравнения итогом выполнения
данной команды (сформированной по ней инструкции) будет результат счета на
вычислителе  или же r.
или же r.
Бесскобочная запись после второго прохода имеет вид
 .
.
Последующие проходы сформируют команды 3 и 4 и бесскобочная запись примет вид
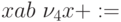 .
.
В результате последующих проходов формируются команды 5 и 6.
Отметим, что команда 6 могла бы иметь вид  , а
бесскобочная запись в этом случае приняла бы вид
, а
бесскобочная запись в этом случае приняла бы вид  . Однако очевидно, что
вместо указания математического адреса вычислителя-исполнителя в команде 6 можно сразу указать
адрес ОП, и по нему должен быть направлен результат операции, который будет
выработан инструкцией, соответствующей команде 6. Поэтому новая команда записи
не формируется, а уточняется команда 6. Вычислитель-исполнитель в ней указан
неявно. Он выбирается с помощью адресного генератора. В связи с этим надо
отметить, что явное задание вычислителей-исполнителей производится лишь в том
случае, когда требуется использование результатов операций в качестве
операндов. Алгоритм работы ПВС не подразумевает обязательного указания в программе о том,
на каком вычислителе будет выполняться операция. Назначение вычислителей
производится автоматически.
. Однако очевидно, что
вместо указания математического адреса вычислителя-исполнителя в команде 6 можно сразу указать
адрес ОП, и по нему должен быть направлен результат операции, который будет
выработан инструкцией, соответствующей команде 6. Поэтому новая команда записи
не формируется, а уточняется команда 6. Вычислитель-исполнитель в ней указан
неявно. Он выбирается с помощью адресного генератора. В связи с этим надо
отметить, что явное задание вычислителей-исполнителей производится лишь в том
случае, когда требуется использование результатов операций в качестве
операндов. Алгоритм работы ПВС не подразумевает обязательного указания в программе о том,
на каком вычислителе будет выполняться операция. Назначение вычислителей
производится автоматически.
Вместе с тем, при необходимости использования имен вычислителей-исполнителей для именования операндов можно формировать имена в широком диапазоне выбора, имеющем два крайних случая.
Можно при каждом новом выборе значения математического адреса вычислителя использовать увеличенную (на единицу) величину ранее использованного значения. Именно так происходит в рассмотренном примере.
Другой крайний случай основан на принципе "экономии" адресов
вычислителей. Он опирается на то, что результат операции используется единственный раз.
Это означает, что и каждое объявленное имя вычислителя используется только
один раз. Поэтому после использования это же имя может объявляться повторно,
и благодаря механизму виртуализации ресурсов никакой коллизии не произойдет.
Так, в команде 3 для обозначения вычислителя-исполнителя вместо  можно
использовать математический адрес
можно
использовать математический адрес  . Вместо
. Вместо  в команде 4 повторно можно
использовать адрес
в команде 4 повторно можно
использовать адрес  и т.д.
и т.д.

