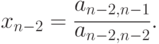Программирование задач для асинхронной ВС архитектуры "data flow"
Решение системы линейных уравнений методом Гаусса
Суть метода заключается в сведении системы линейных уравнений с помощью линейных преобразований к ступенчатому виду. Тогда из последнего уравнения находится значение одного неизвестного. Поднимаясь на одно уравнение вверх, с его помощью находим значение другого неизвестного и т.д. Т.е. предполагается некоторый "проход" по уравнениям системы сверху вниз, а затем обратный проход снизу вверх.
Программу составим для произвольного значения n — числа уравнений (неизвестных). Однако для наглядности зафиксируем n=4.
Итак, система уравнений имеет вид
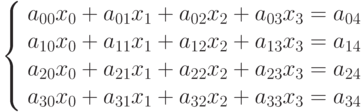
Умножим второе уравнение на r1 = a00 / a10 и вычтем из него первое уравнение. Получим новое уравнение, в котором коэффициенты находятся из выражения
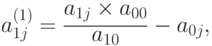
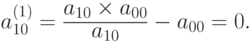
Аналогично, умножая все последующие (k = 2, ...) уравнения на соответствующие величины a00 / ak0 и вычитая первое уравнение, избавимся от вхождения в них переменной x0.
Произведен первый шаг в получении ступенчатой системы уравнений (рис. 11.5).
При этом мы, конечно, считаем, что 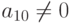 . Если это не
так, но выполняется известное условие существования единственного решения системы, то надо так
переупорядочить (переобозначить) вхождение переменных, чтобы нужный коэффициент
был отличен от нуля. Такое переупорядочение переменных в приведенной ниже
программе предусмотрено.
. Если это не
так, но выполняется известное условие существования единственного решения системы, то надо так
переупорядочить (переобозначить) вхождение переменных, чтобы нужный коэффициент
был отличен от нуля. Такое переупорядочение переменных в приведенной ниже
программе предусмотрено.
На втором шаге вычитаем преобразованное второе уравнение из всех последующих уравнений, предварительно умноженных на r2 = a11(1) / ak1(1). Таким образом мы избавляемся от вхождения в них второй переменной и т.д.
На последнем шаге таких преобразований получаем выражение для нахождения последней переменной. В нашем примере это
a33(3) x3 = a34(3).
Найденное значение x3 подставим в уравнение
a22(2) x2 + a23(2) x3 = a24(2).
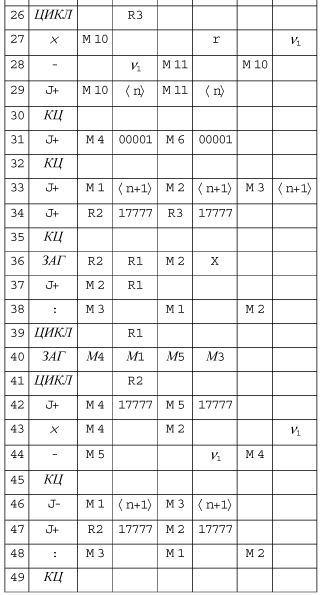
Программа коммутации представлена на рис. 11.6a и 11.6b.
По команде 0 загружаются число переменных в уравнении и адреса
коэффициентов. Команды  производят начальное формирование индексных
регистров.
производят начальное формирование индексных
регистров.
Команда 6 начинает основной цикл на n-1 повторений.
По команде 7 загружаются модификаторы, причем после первого выполнения будут справедливы равенства:
(M4) = a00; (M5) = a11; (M6) = a01.
Команда 8 проверяет равенство a00 = 0 и при несравнении задает переход на выполнение команды 22.
По команде 9 также загружаются модификаторы, и после первого выполнения (при a10 = 0 ) будут справедливы равенства: (M7) = a00; (M8) = a00; (M9) = < l0 >.
По команде 10 начинается вложенный цикл на n - 1, ..., 1 повторений поиска уравнения, у которого старший коэффициент не равен нулю.
По команде 11 производится переход по условию; в первый раз при a10 = 0 — переход к выполнению команды 19.
Команда 12 начинает очередной вложенный цикл. В первый раз выполняются действия:
a00 => l0, a01 => l1 и т.д. (команда 13),
a10 => a00, a11 => a01 и т.д. (команда 14),
l0 => a10, l1 => a11 и т.д. (команда 15) — таким образом, уравнения меняются местами. Выполнение цикла заканчивается по команде 17.
После нахождения старшего ненулевого коэффициента и перестановки уравнений поиск заканчивается, поэтому команда 18 задает принудительный выход из предыдущего цикла.
Команда 19 позволяет произвести переход к анализу следующего уравнения.
Останов по команде 21 означает, что все старшие коэффициенты нулевые и поэтому нельзя построить треугольную матрицу с определителем, не равным нулю.
Команда 22 начинает цикл на n - 1, ..., 1 повторений преобразования уравнений. Команда 24, переход по сравнению, позволяет пропустить уравнение, у которого старший коэффициент равен нулю. Команда 25 коммутирует деление, последовательно задавая вычисление
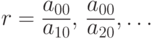
Команда 26 — начало вложенного цикла на n, n - 1, ..., 2 повторений преобразования коэффициентов одного уравнения. В первый раз по командам 27 и 28 будут закоммутированы вычисление и отсылка:

По команде 31 увеличиваются на единицу значения индексных регистров, что позволяет при следующей итерации цикла перейти к анализу следующего уравнения.
Команда 33 в первый раз определяет переход от a00 к a11(1) ; по команде 34 происходит уменьшение граничных значений параметров циклов. Команда 35 — конец самого внешнего цикла, т.е. конец "прямого хода".
По командам 36 и 37 изменяется содержимое индексных регистров:
(M2) = <x0>,\, (l1) = (R2) = n - 1, (M2) = <xn-1>,
а команда 38 коммутирует выполнение операции деления
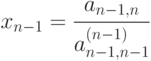
Команда 39 начинает цикл на n - 1 повторение, а команда 41 — вложенный цикл на n - 1, n - 2, ..., 1 повторение.
По командам 43 последовательно в каждой итерации цикла коммутируется выполнение умножения:
an-2, n-1 x xn-1, an-3, n-1 x xn-1 и т.д.,
а по команде 44 — вычитания: an-2,n-1 := an-2, n - an-2, n-1 x xn-1, an-3, n-1 := an-3, n - an-3, n-1 x xn-1 и т.д.
После этого вложенный цикл заканчивается (команда 45), и изменяются значения индексных регистров (команды 46 и 47), что дает возможность перейти к коммутации нахождения xn-2, xn-3 и т.д. (команда 48).
В первый раз