Техника наследования
Как обмануть клиентов
Чтобы понять, как удовлетворить клиентов, мы должны сыграть роль адвокатов дьявола и на секунду представить себе, как их обмануть. Так поступает опытный криминалист, разгадывая преступление. Как мог бы поступить поставщик, желающий ввести в заблуждение своего честного клиента C, гарантирующего при вызове  и ожидающего выполнения
и ожидающего выполнения  Есть два пути:
Есть два пути:
-
Потребовать больше, чем предписано предусловием
 Формулируя более сильное предусловие, мы позволяем себе исключить случаи, которые, согласно исходной спецификации, были совершенно приемлемы.
Формулируя более сильное предусловие, мы позволяем себе исключить случаи, которые, согласно исходной спецификации, были совершенно приемлемы. -
Гарантировать меньше, чем это следует из начального постусловия
 Более слабое постусловие позволяет нам дать в результате меньше, чем было обещано исходной спецификацией.
Более слабое постусловие позволяет нам дать в результате меньше, чем было обещано исходной спецификацией.
| Вспомните, что мы неоднократно говорили при обсуждении Проектирования по Контракту: усиление предусловия облегчает задачу поставщика ("клиент чаще не прав"), иллюстрацией чего служит крайний случай - предусловие false (когда "клиент всегда не прав"). |
Как уже было сказано, утверждение A называется более сильным, чем B, если A логически влечет B, но отличается от него: например, x >= 5 сильнее, чем x >= 0. Если утверждение A сильнее утверждения B, говорят еще, что утверждение B слабее утверждения A.
Как быть честным
Теперь нам понятно, как обманывать. Но как же быть честным? Объявляя подпрограмму повторно, мы можем сохранить ее исходные утверждения, но также мы вправе:
- заменить предусловие более слабым ;
- заменить постусловие более сильным.
Первый подход символизирует щедрость и великодушие: мы допускаем большее число случаев, чем изначально. Это не причинит вред клиенту, который на момент вызова удовлетворяет исходному предусловию. Второй подход означает, что мы выдаем больше, чем от нас требовалось. Это не причинит вред клиенту, полагающемуся на выполнение по завершении вызова исходных постусловий.
Итак, основное правило:
Правило (1) Утверждения Переобъявления (Assertion Redeclaration)
При повторном объявлении подпрограммы предусловие может заменяться лишь равным ему или более слабым, постусловие - лишь равным ему или более сильным.
Это правило отражает тот факт, что новый вариант подпрограммы не должен отвергать вызовы, допустимые в оригинале, и должен, как минимум, представлять гарантии, эквивалентные гарантиям исходного варианта. Он вправе, хоть и не обязан, допускать большее число вызовов или давать более сильные гарантии.
Как явствует из названия, это правило применимо к обеим формам повторного объявления: переопределению и реализации отложенного компонента. Второй случай важен особо, - утверждения будут связаны со всеми эффективными версиями потомков.
Утверждения подпрограммы, как отложенной, так и эффективной, задают ее семантику, применимую к ней самой и ко всем повторным объявлениям ее потомков. Точнее говоря, они специфицируют область допустимого поведения подпрограммы и ее возможных версий. Любое повторное объявление может лишь сужать эту область, не нарушая ее.
Как следствие, создатель класса должен быть осторожным при написании утверждений эффективной подпрограммы, не привнося излишнюю спецификацию (overspecification). Утверждения должны описывать намерения подпрограммы, - ее абстрактную семантику, - но не свойства реализации. Иначе можно закрыть возможность создания иной реализации подпрограммы у будущих потомков.
Пример
Предположим, я написал класс MATRIX, реализующий операции линейной алгебры. Среди прочих возможностей я предлагаю своим клиентам подпрограмму расчета обратной матрицы. Фактически это сочетание команды и двух запросов: процедура invert инвертирует матрицу, присваивает атрибуту inverse значение обратной и устанавливает логический атрибут inverse_valid. Значение атрибута inverse имеет смысл тогда и только тогда, когда inverse_valid является истинным; в противном случае матрицу инвертировать не удалось, так как она вырождена. В ходе нашего обсуждения случай вырожденной матрицы мы можем проигнорировать.
Конечно же, я могу найти лишь приближенное значение обратной матрицы и готов гарантировать определенную точность расчетов, однако, не владея численными подпрограммами в совершенстве, буду принимать лишь запросы с точностью не выше 10-6. В итоге, моя подпрограмма будет выглядеть приблизительно так:
invert (epsilon: REAL) is
-- Обращение текущей матрицы с точностью epsilon
require
epsilon >= 10 ^ (-6)
do
"Вычисление обратной матрицы"
ensure
((Current * inverse) |-| One) <= epsilon
endПостусловие предполагает, что класс содержит инфиксную функцию infix "|-|" такую, что m1 |-| m2 есть |m1 - m2| (норма разности матриц m1 и m2 ), а также функцию infix "*", результатом которой является произведение двух матриц. One - единичная матрица.
Как человек негордый, летом я приглашу программиста, и он перепишет мою подпрограмму invert, используя более удачный алгоритм, лучше аппроксимирующий результат и допускающий меньшее значение epsilon (как повторное объявление, эта запись синтаксически некорректна:
require
epsilon >= 10 ^ (-20)
...
ensure
((Current * inverse) |-| One) <= (epsilon / 2)Автор новой версии достаточно умен, чтобы не переписывать MATRIX в целом. Изменения коснутся лишь нескольких подпрограмм. Они будут включены в состав порожденного от MATRIX класса NEW_MATRIX.
| Если повторное объявление содержит новые утверждения, они должны иметь иной синтаксис, нежели приведенный выше. Правило появится чуть позднее. |
Изменения, внесенные в утверждения, удовлетворяют правилу повторного объявления: новое предусловие epsilon >= 10 ^ (-20) слабее исходного epsilon >= 10 ^ (-6), новое же постусловие сильнее сформулированного вначале.
Вот как все должно происходить. Клиент исходного класса MATRIX запрашивает расчет обратной матрицы именно у него, но на деле - ввиду динамического связывания - вызывает реализацию класса NEW_MATRIX. Тот же клиент может иметь в своем составе подпрограмму
some_client_routine (m1: MATRIX; precision: REAL) is
do
... ; m1.invert (precision); ...
-- Возможен вызов версии как MATRIX, так и NEW_MATRIX
endкоторой один из его собственных клиентов передает первый параметр типа NEW_MATRIX.
NEW_MATRIX должен воспринимать и корректно обрабатывать любой вызов, который принимается его предком. Используя более слабое предусловие и более сильное постусловие, мы корректно обработаем все обращения клиентов MATRIX и предложим своим клиентам решение, лучше прежнего.
При усилении предусловия invert, например, epsilon >= 10 ^ (-5), вызов, корректный для класса MATRIX, мог стать теперь некорректным. При ослаблении постусловия возвращаемый результат стал бы хуже, чем гарантируемый для MATRIX.
Устранение посредника
Последний комментарий указывает на весьма интересное следствие правила Утверждений Переобъявления. В общей схеме
утверждения 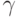 и
и  введенные при повторном объявлении, предпочтительнее для клиентов, если они отличаются от
введенные при повторном объявлении, предпочтительнее для клиентов, если они отличаются от  и
и 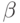 (предусловия - более слабые, постусловия - более сильные). Но клиент класса A, использующий A' благодаря полиморфизму и динамическому связыванию, не может в полной мере воспользоваться более выгодным контрактом, ибо единственный контракт клиента заключен с классом A.
(предусловия - более слабые, постусловия - более сильные). Но клиент класса A, использующий A' благодаря полиморфизму и динамическому связыванию, не может в полной мере воспользоваться более выгодным контрактом, ибо единственный контракт клиента заключен с классом A.
Воспользоваться преимуществом нового контракта можно лишь став непосредственным клиентом A' (пунктирная связь с вопросительным знаком на рисунке 16.3), как в случае:
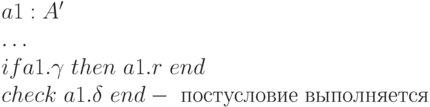
При этом вы, естественно, объявляете a1 как объект типа A', а не объект типа A, как прежде. В результате теряется универсальность полиморфизма, идущая от A.
Компромисс ясен. Клиент класса MATRIX должен обеспечивать выполнение исходного (более сильного) предусловия, а в ответ вправе ожидать выполнения исходного (более слабого) постусловия. Даже если его запрос динамически подготовлен к обслуживанию классом NEW_MATRIX, воспользоваться новыми возможностями - большей толерантностью входа и большей точностью выхода - ему никак не удастся. Для обращения к улучшенной спецификации клиент должен объявить матрицу типа NEW_MATRIX, тем самым, потеряв доступ к иным порожденным от MATRIX реализациям, не являющимся производными классами самого NEW_MATRIX.
Субподряды
Правило Утверждения Переобъявления великолепно сочетается с теорией Проектирования по Контракту.
Мы видели, что утверждения подпрограммы описывают связанный с ней контракт, в котором клиент гарантирует выполнение предусловия, получая право рассчитывать на истинность постусловия; для поставщика все наоборот.
Наследование совместно с повторным объявлением и динамическим связыванием приводит к созданию субподрядов. Приняв условия контракта, вы не обязаны выполнять его сами. Подчас вы знаете кого-то еще, способного сделать это лучше и с меньшими издержками. Так происходит, когда клиент запрашивает подпрограмму из MATRIX, но благодаря динамическому связыванию может на этапе выполнения фактически вызывать версию, переопределенную в потомке. "Меньшие издержки" означают здесь более эффективную реализацию, как в знакомом нам примере с периметром прямоугольника, а "лучше" - усовершенствование утверждений, в описанном здесь смысле.
Правило Утверждения Переобъявления просто устанавливает, что честный субподрядчик, приняв условия контракта, должен выполнить работу на тех же условиях, что и подрядчик или лучших, но никак не худших.
С позиции Проектирования по Контракту, инварианты классов - это ограничения общего характера, применимые и к подрядчикам, и к клиентам. Правило родительских инвариантов отражает тот факт, что все подобные ограничения передаются субподрядчикам.
Свое истинное значение для ОО-разработки наследование приобретает лишь совместно с утверждениями и двумя приведенными выше правилами. Метафора контрактов и субподрядов - прекрасная аналогия, помогающая разрабатывать корректное ОО-ПО. Несомненно, в этом - одна из центральных идей теории проектирования.

