Геометрические преобразования
Задача вращения относительно произвольной оси
Вращение относительно произвольной оси также можно реализовать
посредством умножения матрицы на вектор, но предварительно эту матрицу
надо построить. Предположим, что прямая проходит через начало
координат и задана единичным вектором  , и требуется выполнить поворот
точки на угол
, и требуется выполнить поворот
точки на угол  относительно нее. Для этого воспользуемся следующим
алгоритмом:
относительно нее. Для этого воспользуемся следующим
алгоритмом:
- Совместим прямую с осью
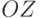 посредством поворота системы координат относительно оси
посредством поворота системы координат относительно оси 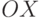 на угол
на угол  , а затем поворота относительно оси
, а затем поворота относительно оси 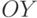 на угол
на угол  .
. - Выполним поворот относительно оси
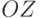 на угол
на угол  .
. - Выполним повороты системы сначала относительно оси
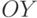 на угол
на угол  , а затем относительно оси
, а затем относительно оси 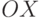 на угол
на угол  (в обратном порядке по отношению к первым поворотам), тем самым возвращая ее в исходное положение.
(в обратном порядке по отношению к первым поворотам), тем самым возвращая ее в исходное положение.
Итоговая матрица преобразования, таким образом, является произведением нескольких матриц, а именно
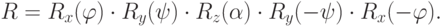
Матрицы  являются матрицами преобразования координат при поворотах
системы координат, как было показано в предыдущем разделе. Определим
сначала угол
являются матрицами преобразования координат при поворотах
системы координат, как было показано в предыдущем разделе. Определим
сначала угол  , который является углом между осью
, который является углом между осью 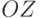 и его проекцией
вектора
и его проекцией
вектора  на плоскость
на плоскость  . Пусть
. Пусть  - длина этой проекции. Тогда
- длина этой проекции. Тогда 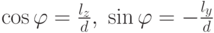 ,
(синус отрицателен, поскольку поворот идет от оси
,
(синус отрицателен, поскольку поворот идет от оси 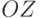 к оси
к оси 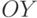 , т.е. в
отрицательном направлении). После поворота системы координат новыми
координатами вектора
, т.е. в
отрицательном направлении). После поворота системы координат новыми
координатами вектора  будут
будут 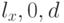 . Угол
. Угол  - это угол между векторами
- это угол между векторами 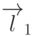 и
и  ,
поэтому
,
поэтому 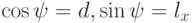 . Теперь мы можем выписать вид матриц преобразования
координат для каждого шага алгоритма, учитывая то, что матрицы
преобразования координат при повороте системы координат обратны по
отношению к соответствующим матрицам вращения:
. Теперь мы можем выписать вид матриц преобразования
координат для каждого шага алгоритма, учитывая то, что матрицы
преобразования координат при повороте системы координат обратны по
отношению к соответствующим матрицам вращения:

Нетрудно убедиться, что последовательное умножение матриц  и
и  на
вектор
на
вектор  дадут в результате вектор
дадут в результате вектор  , т.е. этот вектор действительно
станет осью аппликат.
, т.е. этот вектор действительно
станет осью аппликат.
Остается только выписать окончательный вид матрицы  (для
сокращения записи введем следующие обозначения:
(для
сокращения записи введем следующие обозначения:  ):
):
 |
( 3.19) |
Напомним, что  являются направляющими косинусами прямой,
относительно которой выполняется поворот. Нетрудно убедиться, что если
в качестве осей вращения взять оси координат, то мы в точности получим
формулы (3.10).
являются направляющими косинусами прямой,
относительно которой выполняется поворот. Нетрудно убедиться, что если
в качестве осей вращения взять оси координат, то мы в точности получим
формулы (3.10).
Вопросы и упражнения
- Дайте определение декартовой системы координат.
- Что такое вектор?
- Какие векторы считаются равными?
- Какие векторы называются линейно независимыми?
- Как выразить длину вектора, используя операцию скалярного произведения?
- Как определить косинус угла между векторами, используя операцию скалярного произведения?
- Докажите, что векторное произведение удовлетворяет соотношению
![\alpha[\overrightarrow{r}_1\times\overrightarrow{r}_2]=[\overrightarrow{r}_1\times(\alpha\overrightarrow{r}_2)].](/sites/default/files/tex_cache/4d727cde96fc8ec3b7ba9da3eeaa0631.png)
- Как из произвольного вектора
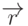 получить единичный вектор, совпадающий с ним по направлению? (Эта операция называется нормировкой вектора ).
получить единичный вектор, совпадающий с ним по направлению? (Эта операция называется нормировкой вектора ). - Каково максимальное число линейно независимых векторов в пространстве?
- Что такое орты?
- Как построить параметрическое уравнение прямой, проходящей через две заданные точки плоскости или пространства?
- Докажите, что если в формуле (3.7) заменить координаты
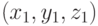 координатами любой другой точки плоскости, то уравнение будет описывать ту же самую плоскость. Указание: возьмите произвольную точку, удовлетворяющую уравнению (3.7), напишите новое уравнение плоскости и покажите, что любая точка второй плоскости принадлежит первой и наоборот.
координатами любой другой точки плоскости, то уравнение будет описывать ту же самую плоскость. Указание: возьмите произвольную точку, удовлетворяющую уравнению (3.7), напишите новое уравнение плоскости и покажите, что любая точка второй плоскости принадлежит первой и наоборот. - В каких случаях луч с плоскостью не пересекаются?
- В каких случаях луч пересекает сферу только в одной точке?
- Исходя из определения умножения матрицы на вектор, докажите, что для любых двух векторов
 и любой матрицы
и любой матрицы  справедливо соотношение
справедливо соотношение
- Докажите, что для любого вектора
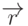 , числа
, числа  и матрицы
и матрицы  справедливо соотношение
справедливо соотношение
- При каком условии масштабирование сохраняет углы между отрезками?
- Какую траекторию описывают точки объекта при повороте?
- Вокруг чего осуществляется поворот на плоскости?
- Вокруг чего осуществляется поворот в пространстве?
- Какие шаги выполняются в алгоритме поворота относительно произвольной оси в пространстве?
- Докажите, что если матрица
 является матрицей поворота, то
является матрицей поворота, то  .
.

