|
С помощью обобщенного алгоритма Евклида найдите числа х и у, удовлетворяющие уравнению 30х +12y = НОД(30,12). х=1, у=-2, НОД = 6. Где ошибка? |
Основные положения теории чисел, используемые в криптографии с открытым ключом
Арифметика остатков и теория сравнений
Немецкий математик Карл Фридрих Гаусс предложил запись

для двух чисел a и b, если они имеют одинаковые остатки от деления на m (читается a сравнимо с b по модулю m ). Например,

Сравнения обнаруживают полезные для математиков и криптографов свойства, во многом похожие на свойства равенств. Эти свойства позволяют существенно упрощать арифметические вычисления, если нас интересует только остаток от деления на некоторое число m. Так, например, свойства сравнений полезны при расчетах в алгоритмах шифрования с открытым ключом.
Простейшими свойствами сравнений являются следующие.
Свойство 1. Если a-b делится на m, то 
Например,  так как 15 -1 =14, а 14 кратно 7.
так как 15 -1 =14, а 14 кратно 7.
Свойство 2. Если

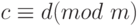

Например, так как  и
и  то
то  а также
а также 
Свойство 3. Если


Например, так как


Свойство 4. Если


Например, известно, что


Свойство 5. Если


Например, если


Малая теорема Ферма
В основе алгоритма шифрования по системе RSA лежит теорема, сформулированная в начале семнадцатого столетия без доказательства французским математиком Пьером Ферма (Pierre Fermat). Её часто называют "Малой теоремой Ферма", и её не следует путать с известной "Великой теоремой Ферма" - её он также сформулировал без доказательства, а доказана она была только в 1993-94 годах. Леонард Эйлер в 1760 году опубликовал доказательство Малой теоремы Ферма и получил ее обобщение, известное под названием теоремы Ферма-Эйлера. Именно эта теорема используется в алгоритме зашифрования/расшифрования RSA.
Малая теорема Ферма формулируется следующим образом. Если p - простое число, а m - любое число, которое не делится на p, то
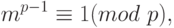
то есть число mp-1 при делении на p дает остаток 1.
Например, пусть р=11, m = 3. Проверим, будет ли 310 mod 11 равно одному:
310 mod 11=32( ((32)2)2mod 11)) = 9(42 mod 11 )= 144 mod 11=1
Обобщение, сформулированное и доказанное Эйлером, справедливо для любого модуля, но в системе RSA используется частный случай, когда модуль является произведением только двух различных простых чисел. Поэтому рассмотрим формулировку теоремы для этого случая.
Теорема Ферма-Эйлера (для случая системы RSA). Если p и q - два различных простых числа, а m - любое число, которое не делится на p и q, то

Например, пусть р=11, q = 5 (pq = 55), m = 3. Проверим, будет ли

равно одному:
340 mod 55 = (35) 4mod 55 = 234 mod 55 = 279841 mod 55 = 1.
Наибольший общий делитель
Пусть а и b — два целых положительных числа. Наибольший общий делитель чисел а и b есть наибольшее число с, которое делит и а, и b:
с = НОД(a, b).
Например, НОД(25,35) =5.
Для нахождения наибольшего общего делителя можно использовать следующий алгоритм, известный как алгоритм Евклида.
Алгоритм NOD (целые a, b, c);
Начало
1. Пока a<>b выполнять:
1.1.Если a>b то a:=a-b, иначе b:= b-a;
2. c:=a;
Конец.После выполнения алгоритма результат будет содержаться в переменной с.
Поcмотрим, как с помощью алгоритма Евклида вычисляется НОД(18,9):
a: 18 9 b: 9 9 c: 9 9
Здесь каждый столбец представляет собой очередную итерацию алгоритма. Процесс продолжается до тех пор, пока b не станет равным a. Тогда в переменную с записывается ответ, в данном случае 9. Это и будет значение НОД(18,9).
Обобщенный алгоритм Евклида
Для многих криптографических систем, рассмотренных в данной книге, актуален так называемый обобщенный алгоритм Евклида, с которым связана следующая теорема.
Теорема. Пусть а и b — два целых положительных числа. Тогда существуют целые (не обязательно положительные) числа х и у, такие, что
ах + by = НОД(a,b).
Обобщенный алгоритм Евклида служит для отыскания НОД(a, b) и х, у, удовлетворяющих записанному выше уравнению. Введем три строки U = (u1,u2,u3), V = (v1,v2,v3) и T = (t1,t2,t3).
Алгоритм записывается следующим образом (во входных параметрах должно соблюдаться условие a>=b ).
Алгоритм OAE (целые a, b);
Начало
1. U = (a,1,0), V = (b,0,1).
2. Пока v1 <> 0 выполнять:
2.1. q= u1 div v1;
2.2. T=(u1 mod v1, u2 – qv2, u3 – qv3);
2.3. U=V, V=T.
3. U=(НОД(a,b),x,y)).
Конец.После окончания алгоритма результат будет содержаться в строке U. Операция div в алгоритме — это операция целочисленного деления.
Пример. Пусть а = 18, b = 9. Найдем числа х и у, удовлетворяющие уравнению
18х +9y = НОД(18,9).
| q | U | V | T | ||||||
| u1 | u2 | u3 | v1 | v2 | v3 | t1 | t2 | t3 | |
| 18 div 9 = 2 | 18 | 1 | 0 | 9 | 0 | 1 | 18 mod 9 = 0 | 1 - 2*0 = 1 | 0 - 2*1 = -2 |
| 9 | 0 | 1 | 0 | 1 | -2 | ||||
В результате получили U=(НОД(a,b),x,y))= (9,0,1).
Выполним проверку: 18*0 +9*1 = 9 = НОД(18,9).
