Рекурсивные программы
Интересные случаи рекурсии
Хорошо определенные правила кажутся настолько разумными, что мы можем думать, что они являются не только достаточными, но и необходимыми правилами, чтобы рекурсивное определение имело смысл. Это и в самом деле справедливо для первых двух правил.
| R1 | Если все ветви определения являются рекурсивными, то невозможно выработать какой-либо экземпляр, который не был бы уже известен. В случае рекурсивных программ такое определение приводит к бесконечным вычислениям, на практике аварийно заканчивающимся из-за переполнения памяти. |
| R2 | Если рекурсивная ветвь применяется к оригинальному контексту, то она не может выработать экземпляр, который не был бы уже известен. Для рекурсивной программы (например, p(x: T) с ветвью, которая вызывает p(x) для того же x, что и в начальном вызове, и где ничего не менялось), это приводит опять-таки к зацикливанию вычислений. Если речь не идет о программах и вычислениях, то такая ветвь бесполезна. |
Другая ситуация – с правилом R3, где правило требует существования варианта у рекурсии, такого как аргумент n у Hanoi. Некоторые рекурсивные программы, которые завершаются, нарушают это свойство. Приведу два примера. Они не имеют практических применений, но высвечивают общие свойства, которые следует знать.
Функция 91 Маккарти была спроектирована Джоном Маккарти, профессором университета в Стэнфорде, создателем языка Лисп (в котором рекурсия играет центральную роль) и одного из создателей направления, получившего название "Искусственный интеллект". Определим ее следующим образом:
mc_carthy (n: INTEGER): INTEGER
— Функция 91 Маккарти.
do
if n > 100 then
Result := n – 10
else
Result := mc_carthy (mc_carthy (n + 11))
end
end
Для целых n, больших 100, она возвращает значение n – 10. Это понятно. Значительно менее понятно из-за двойного рекурсивного вызова, какое же значение вернет функция для n, меньших 100, в том числе и для отрицательных значений, и вообще – закончатся ли вычисления. Оказывается, что во всех случаях, когда n меньше 100, функция завершает работу и возвращает значение 91, из-за чего функция и получила такое имя. Но очевидного варианта здесь нет, и внутренний рекурсивный вызов использует значение, большее начального n.
Вот еще один пример знаменитой программы и знаменитой проблемы, не получившей решения до настоящего момента:
bizarre (n: INTEGER): INTEGER
— Функция, всегда возвращающая 1 для n нечетного и большего 1.
require
positive: n >= 1
do
if n = 1 then
Result := 1
elseif even (n) then
Result := bizarre (n // 2)
else — для нечетных n, больших 1
Result := bizarre ((3*n + 1) // 2)
end
end
Здесь используются операция // – деление нацело, и булевское выражение even(n), истинное для четных n. Два вхождения этой операции дают точное значение, поскольку применяются к четным числам. Понятно, что если функция возвращает результат, то он может быть только 1, производимой единственной нерекурсивной ветвью. Но завершается ли эта программа для любых n? Ответ кажется очевидным: "да" (можно написать программу и проверить ее на возможном диапазоне чисел. Доказана ее завершаемость на очень больших числах, но общего решения пока нет). Явного варианта рекурсии здесь нет, и видно, что в одной из ветвей рекурсивного вызова аргумент (3*n +1)//2 больше, чем n.
Эти интересные примеры являются экзотикой, но необходимо принимать в расчет их существование для общего понимания рекурсии. Они означают, что существуют некоторые рекурсивные определения, которые не удовлетворяют, казалось бы, разумным методологическим правилам, обсужденным выше, и все же вырабатывают хорошо определенные результаты.
Заметьте, что такие примеры, завершающиеся для каждого возможного аргумента, должны иметь вариант, так как для любого выполнения число рекурсивных вызовов определено и конечно, и следовательно, определяется состоянием программы во время вычисления, так что оно является функцией состояния, которая и может служить вариантом. Беда в том, что эта функция неизвестна, мы не можем ее выразить, а раз так, то ее теоретическое существование мало что дает практике.
На практике мы такие примеры оставляем без внимания и ограничиваем себя рекурсивными определениями, которые обладают всеми тремя свойствами – R1, R2, R3. В частности, когда вы пишете рекурсивную программу, следует всегда, как в оставшихся примерах этой лекции, явно задавать вариант в рекурсии.
Определения, не требующие творчества
Даже с хорошо определенными правилами и наличием варианта у рекурсии мы все же не можем спать спокойно, используя рекурсию. Проблема в том, что рекурсивное определение не является определением в обычном смысле, поскольку оно может быть креативным – творческим.
Аксиома в математике является креативной: она говорит нам нечто такое, что не может быть выведено из известных уже фактов. Примером является аксиома о целых в математике, которая говорит, что для числа n', следующего за n, справедливо n < n'. Фундаментальные законы в естественных науках также креативны, например, закон, утверждающий о невозможности двигаться со скоростью, превышающей скорость света.
Теоремы в математике, так же как и аналогичные результаты в физике, с рассматриваемой точки зрения "творческими" не являются, поскольку могут быть выведены из аксиом и известных уже законов. Они интересны сами по себе и позволяют нам более просто выводить новые утверждения, но они не добавляют новых предположений, являясь следствиями уже сделанных ранее.
Определение, так же как и теорема, не должно быть творческим. Определение дает новое имя объекту нашего мира, но все утверждения, которые можно выразить с использованием определения, могут быть сделаны и без помощи этого определения. Мы хотим более просто выражать утверждения, используя введенное определение, а иначе зачем бы понадобилось его вводить. Но мы знаем, что можно обойтись и без определения. Пусть сказано:

Ничего нового такое определение в математику не добавляет: просто разрешается использовать новую нотацию для умножения. Любое свойство, которое может быть доказано с использование новой нотации, может быть доказано и без нее, по сути, заменой  в соответствии с определением.
в соответствии с определением.
Символ  , который мы использовали для обозначения "определено как" (начиная с БНФ-продукционных правил грамматики) предполагает этот некреативный характер определения. Но давайте рассмотрим рекурсивное определение в форме:
, который мы использовали для обозначения "определено как" (начиная с БНФ-продукционных правил грамматики) предполагает этот некреативный характер определения. Но давайте рассмотрим рекурсивное определение в форме:
 |
( 5.1) |
Здесь some_expression включает f. Теперь наш принцип больше не выполняется! Всякая попытка заменить f в определении some_expression на some_expression не устраняет f, так что реально мы ничего не определили. До тех пор, пока мы не найдем удобного, некреативного смысла для определений, подобных формуле (5.1), мы должны быть терминологически аккуратны. По этой причине символ  будет использоваться только для нерекурсивных определений, а такое свойство, как (5.1), будет задаваться равенством
будет использоваться только для нерекурсивных определений, а такое свойство, как (5.1), будет задаваться равенством
 |
( 5.2) |
Это равенство можно рассматривать как уравнение, решением которого выступает f. Говоря о рекурсивных "определениях", для корректности будем заключать второе слово в кавычки.
Взгляд на рекурсивные "определения" снизу вверх
Изолировав пока рекурсию и поместив ее в карантинную зону, полезно посмотреть на рекурсивные программы и рекурсивные "определения" в целом с позиции "снизу вверх". Я надеюсь, что это удалит легкое головокружение, которое остается, когда видишь определения программ, которые – частично – сами себя вызывают.
Рекурсивные "определения" пишутся "сверху вниз", определяя смысл понятия в терминах того же понятия для "меньшего" контекста – меньшего с точки зрения варианта рекурсии. Например, Fibonacci для n выражается через Fibonacci для n – 1 и n – 2.
Взгляд "снизу-вверх" предоставляет другую интерпретацию того же определения, трактуя это другим способом, как механизм, который создает новое значение на основе уже существующих. Начнем с рассмотрения функции. Для любой функции f можно построить граф этой функции как множество пар [x, f(x)] для каждого применимого x. Граф для функции Fibonacci задается множеством
![F\triangleq \{[0, 0], [1, 1], [2, 1], [3, 2], [4, 3], [5, 5], [6, 8], [7, 13] …\}](/sites/default/files/tex_cache/6b38e97de8f5994ee91d35475c9aa6e5.png) |
( 5.3) |
Он содержит все пары [n, Fibonacci(n)] для всех неотрицательных n. Этот граф содержит всю информацию о функции. Визуально этот граф можно представить в следующей форме:
В верхней строчке показаны возможные аргументы функции, в нижней – соответствующие значения функции.
Дать функции рекурсивное определение – это все равно, что сказать, что ее граф F – как множество пар – удовлетворяет некоторому свойству
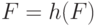 |
( 5.4) |
Здесь h рассматривается как некоторая функция, применимая к такому множеству пар. Это подобно уравнению, которому F должна удовлетворять, и известному как уравнение неподвижной точки. Неподвижной точкой – решением такого уравнения – является некоторый математический объект, в данном случае функция, который остается инвариантом при некоторых трансформациях, в данном случае – задаваемых функцией h.
Определим рекурсивно функцию Fibonacci:

Такое определение эквивалентно тому, что граф F, рассматриваемый как множество пар, удовлетворяет уравнению неподвижной точки (5.4), где h – это функция, которая, получив множество пар, вырабатывает новое множество, содержащее следующие пары:
Мы можем использовать эту точку зрения, чтобы дать рекурсивному "определению" точный смысл, свободный от всякой рекурсивной загадочности. Мы начинаем с графа  , который пуст (не содержит пар). Далее мы определяем
, который пуст (не содержит пар). Далее мы определяем
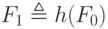
Оно имеет смысл и означает, что  задается множеством {[0, 0], [1, 1]} – парами, определяемыми правилами G2 и G3. Правила G1 и G4 в данном случае неприменимы, так как
задается множеством {[0, 0], [1, 1]} – парами, определяемыми правилами G2 и G3. Правила G1 и G4 в данном случае неприменимы, так как  пусто. Затем мы снова применяем
пусто. Затем мы снова применяем 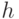 , чтобы получить
, чтобы получить
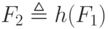
Здесь G2 и G3 нам не дают ничего нового, так как пары [0, 0] и [1, 1] уже присутствуют в  , но G4 создает новую пару из существующих – [2, 1]. Продолжая, мы определяем последовательность графов, начиная с
, но G4 создает новую пару из существующих – [2, 1]. Продолжая, мы определяем последовательность графов, начиная с  и определяя
и определяя 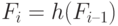 . Теперь рассмотрим
. Теперь рассмотрим  как бесконечное объединение:
как бесконечное объединение:

Здесь  – это множество натуральных чисел. Достаточно просто видеть, что
– это множество натуральных чисел. Достаточно просто видеть, что  удовлетворяет свойству (5.4).
удовлетворяет свойству (5.4).
Такова нерекурсивная интерпретация – семантика, – которую мы дали рекурсивному "определению" функции Fibonacci.
В общем случае уравнение неподвижной точки в форме (5.4) на графах функции, устанавливающее эквивалентность  и
и  , представляет решение в виде графа функции
, представляет решение в виде графа функции

Здесь  – это последовательность графов функции:
– это последовательность графов функции:

Подход, основанный на неподвижной точке, является базисом интерпретации "снизу вверх" рекурсивных вычислений. Он частично удаляет загадочность из этих определений, поскольку рассматривает рекурсивное определение как уравнение неподвижной точки и допускает решение, полученное как результат объединения (подобно пределу последовательности в математическом анализе) последовательности графов функции.
 , никогда бы не создавала новых пар, поскольку во всех случаях определения
, никогда бы не создавала новых пар, поскольку во всех случаях определения 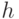 , подобно G1 и G4 для Фибоначчи, новые пары создаются из существующих, а их нет в пустом множестве.
, подобно G1 и G4 для Фибоначчи, новые пары создаются из существующих, а их нет в пустом множестве.Данный подход редуцирует рекурсивное "определение" к хорошо известному, традиционному понятию индуктивного определения последовательности.
Функция Фибоначчи является хорошим примером для понимания концепции, но, вероятно, она не поражает впечатления. Во всех учебниках по математике она определяется индуктивно как последовательность чисел. Это в компьютерном мире мы рассматриваем ее как рекурсивную функцию. Так что мы не узнали ничего нового о самой функции, а просто познакомились с разными точками зрения. Давайте посмотрим, можно ли научиться чему-нибудь на других примерах.
Интерпретация "снизу вверх" конструктивных определений
Понимая природу "снизу вверх", можно дать ясное понимание смысла рекурсивного определения понятия "тип". Как вы помните, тип определяется следующим образом:
| T1 | базисный класс, такой как INTEGER или STATION; |
| T2 | родовое порождение в форме C [T], где C является универсальным классом и T – это тип. |
Правило T1 определяет нерекурсивный случай. Взгляд "снизу вверх" позволяет нам понимать данное определение как построение множества типов в виде последовательности слоев. Ограничившись для простоты одним родовым параметром, имеем:
- слой L0 включает все типы, построенные из базисных классов: INTEGER, STATION и т.д.;
- слой L1 имеет все типы в форме C [X], где C универсальный класс, а X принадлежит уровню L0: LIST [INTEGER], ARRAY [STATION] и т.д.;
- в общем случае слой Ln для любого n > 0 имеет все типы в форме C [X], где X принадлежит уровню Li для i < n.
Таким образом, мы получаем все типы – базисные и полученные в результате родового порождения.
Башни, "снизу вверх"
Взглянем теперь "снизу вверх" на Ханойские башни. Программу можно рассматривать как рекурсивное определение последовательности ходов. Давайте обозначим такую последовательность как  , означающую, что первым ходом переносится диск с вершины стержня А на B, затем с C на A и так далее. Пустая последовательность будет
, означающую, что первым ходом переносится диск с вершины стержня А на B, затем с C на A и так далее. Пустая последовательность будет  , а конкатенация последовательностей задается знаком "+", так что
, а конкатенация последовательностей задается знаком "+", так что

Тогда мы можем выразить рекурсивное решение как функцию han с четырьмя аргументами (целое и три стержня), вырабатывающую последовательность ходов и удовлетворяющую уравнению неподвижной точки
 |
( 5.5) |
 |
( 5.6) |
Функция определена, если  положительно и значения
положительно и значения  ,
,  ,
,  (сокращения для source, target, other) различны – мы используем их, как и ранее, для обозначения стержней 'A', 'B', 'C'. Конструирование функции, решающей уравнение, просто: (5.5) позволяет инициализировать граф функции для
(сокращения для source, target, other) различны – мы используем их, как и ранее, для обозначения стержней 'A', 'B', 'C'. Конструирование функции, решающей уравнение, просто: (5.5) позволяет инициализировать граф функции для 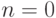 в следующей форме:
в следующей форме:
![[(0, s, t, o), < > ]](/sites/default/files/tex_cache/6455a3af8f501bbf5468bfc5c6bb05e1.png)
Обозначим через  эту первую часть графа, содержащую 6 пар, которые включают все возможные перестановки стержней. После этого можно использовать (5.6) для получения множества пар
эту первую часть графа, содержащую 6 пар, которые включают все возможные перестановки стержней. После этого можно использовать (5.6) для получения множества пар  , содержащего значения для
, содержащего значения для  , где пары имеют вид:
, где пары имеют вид:
![[(1, s, t, o), <s\to t>]](/sites/default/files/tex_cache/4f2c82b73396beeab99b0a2c6fbb8282.png)
Здесь учитывается, что конкатенация 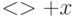 или
или  дает
дает  . Следующая итерация (5.6) даст нам
. Следующая итерация (5.6) даст нам 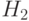 , чьи пары имеют вид:
, чьи пары имеют вид:
![[(2, s, t, o), fl + <s\to t> + gl]](/sites/default/files/tex_cache/6cc5bdc4ab47dc3e45346068b087df26.png)
Это верно для всех  таких, что
таких, что  содержит как пару
содержит как пару ![[(1, s, o, t), f1]](/sites/default/files/tex_cache/c16287ec9f2734093453166b3e7e7b37.png) , так и пару
, так и пару ![[(1, o, t, s), g1]](/sites/default/files/tex_cache/e0a48465bf3a1bf96acad753f7f4555e.png) .
.
Последующее итерирование позволит построить граф  . Полный граф – разумеется, бесконечный, поскольку включает пары для всех возможных
. Полный граф – разумеется, бесконечный, поскольку включает пары для всех возможных  , – задает множество всех пар во всех элементах последовательности:
, – задает множество всех пар во всех элементах последовательности:

Теперь я смею надеяться, что вы получили достаточное представление о подходе "снизу вверх" к рекурсивным вычислениям и сможете написать программу построения графа.
Время программирования!
Напишите программу (не используя рекурсии), создающую последовательно элементы множеств 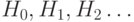 для Hanoi.
для Hanoi.
Связанное с этой задачей упражнение попросит вас определить (без программирования) математические свойства графа.
Еще одно важное упражнение потребует применить подобный анализ к обходу бинарного дерева. Вы должны будете спроектировать модель для представления решения, подобную той, что использована в данной задаче, – вместо последовательности ходов должна появиться последовательность узлов.
Грамматики как рекурсивно определенные функции
Подход "снизу вверх", в частности, применим и для рекурсивных грамматик, как в нашем небольшом примере:

Здесь введены сокращения: ifc представляет "if Condition then" и ast представляет "Assignment", оба рассматриваются как терминалы в данном обсуждении.
Достаточно просто видеть, как генерировать последовательные предложения языка, интерпретируя создаваемые продукции в стиле неподвижной точки:

Генерация продукций может быть продолжена
С этих же позиций может быть проанализировано предыдущее обсуждение небольшого языка Game.
Данный подход обобщается на произвольные грамматики, рассматривая матричное представление описания БНФ.

