Общие динамические системы
Практическое занятие "Управляемые динамические системы"
Цель занятия
Провести вычислительные эксперименты с управляемыми динамическими системами, заданными дифференциальными уравнениями.
Практическая задача
Рассмотрим динамическую систему, заданную дифференциальным уравнением
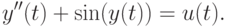
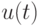. Мы будем рассматривать эту задачу с
нулевыми начальными условиями. При этом решение 
удовлетворяет однородному уравнению.Сначала посмотрим на решение этого уравнения, когда управление 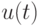является постоянным и имеет вид
![u(t)=1,\quad t\in[0,10].](/sites/default/files/tex_cache/e1f5dbdf3c227f4ef1dde9ea4ccd33ee.png)
![\begin{verbatim}
class TTest1RK : TRungeKutta
{
public TTest1RK() : base(2) { }
public override void F(double t, double[] Y,
ref double[] FY)
{
FY[0] = Y[1];
FY[1] = -Math.Sin(Y[0]) + 1;
}
}
\end{verbatim}](/sites/default/files/tex_cache/84a74be4b5cdd68cd4c4c316e0b63dd6.png)
Работать с этим классом мы будем следующим образом.
![\begin{verbatim}
double h = 0.01;
double[] Y0 = { 0, 1.0 };
TTest1RK Test1RK = new TTest1RK();
Test1RK.SetInit(0, Y0);
StreamWriter F = File.CreateText("test1.txt");
double t, Euler, RK, Sin;
while (Test1RK.GetCurrent() < (10 + h / 2.0))
{
t = Test1RK.GetCurrent();
RK = Test1RK.Y[0];
F.WriteLine("{0}\t{1}", t, RK);
Test1RK.NextStep(h);
}
F.Close();
\end{verbatim}](/sites/default/files/tex_cache/54d471fc099ea38a1458ddfb71499bf2.png)
Мы видим, что в данном случае решение монотонно и довольно быстро возрастает с ростом времени.
Теперь в качестве управления возьмем функцию
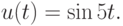
Теперь в качестве уравнения мы возьмем уравнение описывающее осцилятор Ван-дер-Поля
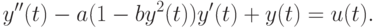
![\begin{verbatim}
class TTestPoleRK : TRungeKutta
{
double a, b;
public TTestPoleRK(double a, double b)
: base(2)
{
this.a = a;
this.b = b;
}
public override void F(double t, double[] Y, ref double[] FY)
{
FY[0] = Y[1];
FY[1] = a * (1 - b * Y[0] * Y[0]) * Y[1] - Y[0] + 0.01;
}
}
\end{verbatim}](/sites/default/files/tex_cache/1150b1b606927137f63875628087f5ee.png)
Использование в качестве управления постоянной дает нам решение, которое совершает колебания со все увеличивающейся амплитудой.
Теперь в качестве управляющей функции мы возьмем кратковременно действующий импульс
