Oбъектно-opиентированное управление решениями дифференциальных уравнений
На рисунке 18.1 мы приводим фазовый портрет нашей управляемой системы. Угловые точки на траектории отражают моменты переключения управления. Мы видим, что траектория быстро сходится к искомому предельному циклу. Предельным циклом называется периодическая (замкнутая) траектория в окрестности которой нет других периодических траекторий.
Заметим, что хотя наше уравнение маятника является линейным
относительно неизвестной функции 
и управление входит в это
уравнение линейно, но зависимость решения от управления является
уже нелинейной. Эта ситуация является общей для систем управления.
Другой пример управляемой системы состоит в следующем. Будем рассматривать простейшую систему автопилота самолета. Мы будем управлять курсовым углом самолета. Пусть нам задан нулевой курс. В линейном приближении колебания этого курса описываются системой дифференциальных уравнений:
![\begin{verbatim}
class TPilotControl : TControlSystem
{
public TPilotControl()
: base(2, 1)
{
U[0] = 1;
}
public override void SetU()
{
if (Y[0] < 0)
{
U[0] = 1;
}
else
{
U[0] = -1;
}
}
public override void F(double t, double[] Y,
ref double[] FY)
{
FY[0] = Y[1];
FY[1] = -Y[1] + U[0];
}
}
\end{verbatim}](/sites/default/files/tex_cache/57265576e28a1a0aaae9638817c2144e.png)
И проведем вычислительный эксперимент с нашим управлением.
![\begin{verbatim}
TPilotControl Pilot = new TPilotControl();
Pilot.SetInit(0, new double[2] { 1, 0 });
F = File.CreateText("pilot.txt");
while (Pilot.GetCurrent() < 50.0 + h / 2.0)
{
Console.WriteLine("{0}\t{1}\t{2}\t{3}",
Pilot.GetCurrent(), Pilot.Y[0], Pilot.Y[1], Pilot.U[0]);
F.WriteLine("{0}\t{1}\t{2}\t{3}",
Pilot.GetCurrent(), Pilot.Y[0], Pilot.Y[1], Pilot.U[0]);
Pilot.NextStep(h);
}
F.Close();
\end{verbatim}](/sites/default/files/tex_cache/e8aac69b55fc4757d5ddac9c76e824c5.png)
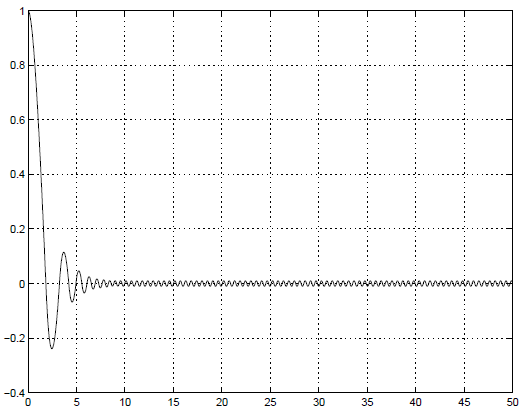
В результате на рисунке 18.2 мы получим колебания нашего курса. Можно видеть, что довольно быстро амплитуда колебаний нашего курса становится малой, однако в нашей системе возникли характерные автоколебания. Автоколебаниями называются незатухающие периодические колебания. При этом частота этих колебаний определяется свойствами самой нелинейной системы, а не частотой внешнего воздействия. Предельный цикл является одним из примеров автоколебаний.
Ключевые термины
Множество допустимых управлений - множество, которому принадлежит управление.
Управляемая система - система, описывающаяся дифференциальным и уравнениями, содержащие управление.
Целевой функционал - функционал на решении, с помощью которого определяется оптимальное решение.
Краткие итоги: Рассмотрены методы управления дифференциальными уравнениями с помощью выбора правых частей. Проведены вычислительные эксперименты, позволяющие дать качественную картину некоторых задач управления.