Современные численные методы в объектно-ориентированном изложении на C#
[+]
Лекция 16:

Приближение сплайнами
A
|
версия для печати
< Лекция 15 || Лекция 16: 123 || Лекция 17 >

Лабораторная работа "Аппроксимация функций"

Цель занятия

Практическое проведение интерполяции для конкретных функций и изучение свойств интерполяционных функций.

Сценарий лабораторной работы

  1. Напишите программу на языке C# для построения и вычисления интерполяционного многочлена в форме Лагранжа для произвольных функций и точек разбиения.
  2. Проведите вычислительные эксперименты на примере тригонометрических функций. В этих экспериментах рассчитайте погрешность интерполяционной функции.
  3. Выясните зависимость погрешности интерполяции в зависимости от использования равномерного и неравномерного разбиения отрезка.

Указания

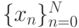Если на отрезке [a,b] задана некоторая числовая функция f(x), то разбиением отрезка [a,b] называется конечное множество точек \{x_n\}_{n=0}^N таких, что

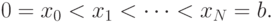
0=x_0<x_1<\dots<x_N=b.
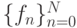Если также на ряду с разбиением отрезка нам дан набор чисел \{f_n\}_{n=0}^N, который имеет смысл значений функции в узловых точках
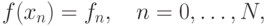
f(x_n)=f_n,\quad n=0,\dots,N,
то возникает задача о построении интерполяционного многочлена.

Интерполяционный многочлен в форме Лагранжа может быть найден по формуле

P_N(x)=\sum\limits_{i=0}^Np_N^i(x)f_i,
где
p_N^i(x)=\frac{(x-x_0)\cdots(x-x_{i-1})(x-x_{i+1})\cdots(x-x_N)} {(x_i-x_0)\cdots(x_i-x_{i-1})(x_i-x_{i+1})\cdots(x_i-x_N)}.

Дальше >>
< Лекция 15 || Лекция 16: 123 || Лекция 17 >

Вопросы и ответы

вопросов: 0