НОУ ИНТУИТ | Разработка телетрафика и планирование сетей. Лекция 13: Системы с ожиданием

Учитесь и получайте официальные документы БЕСПЛАТНО. Вы можете поддержать наш проект.

Регистрация Вход

Твой путь к знаниям!

Опубликован: 20.04.2011 | Доступ: свободный | Студентов: 1059 / 207 | Оценка: 4.36 / 4.36 | Длительность: 22:21:00

Тема: Сетевые технологии

Специальности: Администратор коммуникационных систем, Архитектор программного обеспечения

|

Вам нравится? Нравится 14 студентам

| Поделиться |

Поддержать курс

| Скачать электронную книгу

Принцип Мо для систем с ожиданием

Mo сначала предложил свой принцип для систем организации очереди. Он изучил времена ожидания абонентов для оператора на ручных станциях Копенгагенской Телефонной Компании.

Рассмотрим независимости систем организации очереди. Вызов, обслуживаемый во всех системах, имеет полное среднее времени ожидания

$\sum_i W_i,$

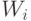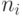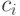где W_i - среднее время ожидания -той системы, которая имеет n_i обслуживающих приборов и предложенную нагрузку A_i. Стоимость канала равна переменной стоимости c_i плюс постоянная стоимость, выраженная константой C_0. Таким образом, общая стоимость каналов равна:

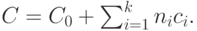$C=C_0+\sum_{i=1}^kn_ic_i.$

( 12.23)

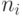Если время ожидания также рассматривать как стоимость, то общая стоимость будет равна $f=f (n_1, n_2 , \dots, n_k )$ . Она должна быть свернута как функция числа n_i каналов в отдельные системы. Если полное среднее время ожидания - 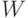, то распределение каналов по отдельным системам определяется:

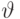$min\{f(n_1, n_2, \dots, n_k)\}=min \{C_0+\sum_in_ic_i+ \vartheta *\left(\sum_iW_i-W \right) \}$

( 12.24)

где $\vartheta$ (тета) - множитель Лагранжа.

Величина 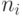n_i является неотъемлемой частью необходимого условия для определения минимума, и можно показать, что в этом случае достаточным условием для минимума являются следующие неравенства :

$0 < f(n_1, n_2, \dots, n_i-1, \dots, n_k)-f(n_1, n_2, \dots, n_i, \dots, n_k),\\ 0 \ge f(n_1, n_2, \dots, n_i, \dots, n_k)-f(n_1, n_2, \dots, n_i+1, \dots, n_k),$

( 12.25)

что соответствует:

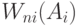$W_{n_i-1}(A_i)-W_{n_i}(A_i) > \frac{c_i}{\vartheta},\\ W_{n_i}(A_i)-W_{n_i+1}(A_i) \le \frac{c_i}{\vartheta},$

( 12.26)

где $W_{ni} (A_i )$ показано в (12.15).

Выраженное с помощью функции увеличения времени ожидания $F_{W,n} (A)$ (12.22) оптимальное решение равно:

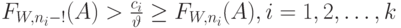$F_{W,n_i-!}(A) > \frac{c_i}{\vartheta} \ge F_{W, n_i}(A), i=1,2,\dots, k$

( 12.27)

Функция 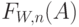$F_{W, n} (A)$ сведена в таблицу в Принципе Мо (Jensen, 1950 [50] ). Подобная оптимизация может быть проведена для других функций увеличения.

Пример 12.3.1: Система с ожиданием

Мы рассматриваем две различных 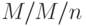M/M/n системы организации очереди. Первая имеет среднее время обслуживания 100 с и предложенную нагрузку 20 Эрл. Отношение стоимости 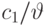$c_1/ \vartheta$ равно 0,01. Вторая система имеет среднее время обслуживания, равное 10 с, и предложенную нагрузку 2 Эрл. Отношение стоимости равняется 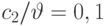$c_2 /\vartheta = 0,1$ . Таблица функции увеличения 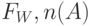F_W,n (A) дает:

n_1 = 32 канала и

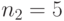n_2 = 5 каналов.

Средние времена ожидания:

Это показывает, что вызов, который обслуживается в обеих системах, имеет полное среднее время ожидания 0,274 с и что система с меньшим количеством каналов вносит больший вклад в среднее время ожидания.

Стоимость ожидания связана с отношением стоимости. Инвестируя больше в вышеупомянутую систему, мы уменьшаем затраты независимо от системы организации очереди. Необходимо идти на вложения, пока получаем прибыль. Исследования Мо в течение 1920-ых годов показали, что среднее время ожидания для абонентов маленьких станций с немногими операторами должно быть большим, чем среднее время ожидания при больших станциях со многими операторами.

Распределение времени ожидания для M/M/n при дисциплине FCFS

Системы организации очереди, где дисциплина обслуживания зависит от времени поступления вызовов, все имеют одни и те же средние времена ожидания. В этом случае стратегия влияет только на распределение времен ожидания для каждого отдельного клиента. Исследование распределения времени ожидания упрощается в случае дисциплины FCFS (First Come First Served - "Первый прибыл - Первый обслужен"). Эта же дисциплина обозначается FIFO (First In First Out). Она также называется дисциплина обслуживания в порядке поступлении. Но если обслуживающих приборов много, заявка может не обязательно покинуть обслуживающий прибор первой. Тогда дисциплина в порядке поступления рассматривается в соответствии с принципом, чтобы время выхода из очереди и начало освобождения обслуживающего прибора была началом обслуживания другой заявки.

Рассмотрим произвольный вызов. По прибытию в систему вызов или обслуживается немедленно, или должен ждать в очереди (12.6).

Предположим, что вызов, который мы рассматриваем, должен ждать в очереди, то есть система может быть в состоянии $[n + k], (k = 0, 1, 2, \dots)$ , где - число занятых мест ожидания как раз перед поступлением вызова.

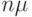Наш вызов должен ждать, пока будет завершено обслуживание k + 1 вызовов, прежде чем станет доступным свободный обслуживающий прибор. Когда все обслуживающих приборов работают, система завершает обслуживание вызовов с постоянной скоростью $n \mu$ , то есть процесс выхода вызовов из обслуживания является Пуассоновским процессом с данной интенсивностью. Мы используем отношения между числовым представлением и представлением с помощью интервала (5.4). 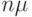Вероятность $p(W \le t) = F(t)$ , что положительное время ожидания превосходит заданную величину, равна вероятности того, что в Пуассоновском потоке вызовов с интенсивностью $n \mu$ , по крайней мере, (k+1) вызовов поступят в течение интервала (6.1):

$F(t|k \quad waiting)=\sum_{i=n+1}^{\infty} \frac{(n \mu t)^i}{i!}*e^{-n \mu t}.$

( 12.28)

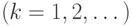Вышеупомянутое равенство справедливо при условии, что наш вызов должен ждать в очереди. Условная вероятность, что наш вызов поступит, когда все обслуживающих приборов заняты и имеется обслуживаемых вызовов $(k=1,2, \dots)$ , такова:

$p_w(k)=\frac{\lambda p(n+k)}{\lambda \sum_{i=0}^{\infty}p(n+i)}=\frac{p(n)*(\frac An)^k}{p(n)*\sum_{i=0}^{\infty}(\frac An)^i}\\ =(1- \frac An)(\frac An)^k, k=0,1, \dots.$

( 12.29)

Это геометрическое распределение, включая нулевой класс (табл. 6.1). Безусловное распределение времени ожидания тогда равно:

$F(t)=\sum_{k=0}^{\infty}p_w(k)*F(t|k),$

( 12.30)

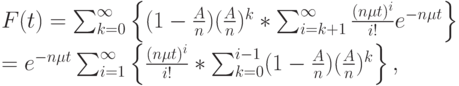
$F(t)=\sum_{k=0}^{\infty} \left \{(1-\frac An)(\frac An)^k*\sum_{i=k+1}^{\infty} \frac{(n \mu t)^i}{i!}e^{-n \mu t} \right \}\\ =e^{-n \mu t}\sum_{i=1}^{\infty} \left \{ \frac{(n \mu t)^i}{i!}*\sum_{k=0}^{i-1}(1-\frac An)(\frac An)^k \right \},$

Когда все элементы - положительные вероятности, мы можем поменять порядок суммирования. Внутренняя сумма является геометрической прогрессией:

$\sum_{k=0}^{i-1}(1-\frac An)(\frac An)^k=(1-\frac An)*\sum_{k=0}^{i-1}(\frac An)^k\\ =(1-\frac An)*1*\frac{1-(A/n)^i}{1-(A/n)}\\ =1-(\frac An)^i.$

Подставляя результат этой суммы, мы получаем:

$F(t)=e^{-n \mu t}* \sum_{i=1}^{\infty} \frac{(n \mu t)^i}{i!} \left \{1-(\frac An)^i \right \}\\ =e^{-n \mu t} \left \{ \sum_{i=0}^{\infty} \frac{(n \mu t)^i}{i!}-\sum_{i=0}^{\infty} \frac{(n \mu t)^i}{i!} (\frac An)^i \right \}\\ =e^{n \mu t}\{e^{n \mu t}-e^{n \mu t*A/n}\},$

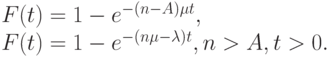$F(t)=1-e^{-(n-A)\mu t},\\ F(t)=1-e^{-(n \mu - \lambda)t}, n > A, t > 0.$

( 12.31)

то есть экспоненциальное распределение. Очевидно, существует парадокс - при поступлении вызова в систему со всеми ранее занятыми обслуживающими приборами можно:

рассчитать число ждущих клиентов. Полное время ожидания тогда будет 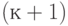- Эрланговское распределение;
если не учитывать этих ждущих клиентов, то время ожидания становится экспоненциально распределенным.

Интерпретация этого факта - то, что взвешенная сумма распределений Эрланга с геометрически распределенными коэффициентами веса эквивалентна экспоненциальному распределению. На рис.12.3 показана диаграмма состояний для (12.30), и мы можем заметить, что она может быть сведена к единственному экспоненциальному распределению (секция 4.4.2 и рис.4.9). Формула (12.31) подтверждает, что среднее время ожидания w_n для клиентов, которые должны ждать в очереди, определяется выражением, показанным в (12.17).

Рис. 12.3.

Распределение общее время ожидания (для произвольного вызова) равно (3.19):

$F_s(t)=1-E_{2,n}(A)*e^{-(n-A)\mu t}, A < n, t \ge 0,$

( 12.32)

и средняя величина этого распределения - W_n, в соответствии с (12.15).

Время пребывания в системе в случае одного обслуживающего прибора

Когда имеется только один обслуживающий прибор, вероятности состояния (12.2) представляются рядом геометрической прогрессии 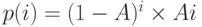$p(i)=(1 -A)^i \times Ai$ (12.18) для всех $i \ge 0$ . Каждый вызов занимает экспоненциально распределенный временной интервал с интенсивностью $\lambda$ в каждом состоянии. Вызов, который поступает в систему в состоянии [i] , должен остаться в системе, интервал времени распределен по закону Эрланга - (i+1) . Поэтому время пребывания в системе (время ожидания + время обслуживания), которое также называется временем реакции, является экспоненциально распределенным с интенсивностью $(\mu - \lambda)$ . (см. рис. 4.9):

$F(t)=1-e^{-(\mu - \lambda)t}, \mu > \lambda, t \ge 0.$

( 12.33)

Это идентично распределению времени ожидания задержанных вызовов. Среднее время пребывания может быть получено непосредственно, используя W_1 из(12.20) и среднее время обслуживания :

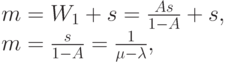$m=W_1+s=\frac{As}{1-A}+s,\\ m=\frac{s}{1-A}=\frac{1}{\mu - \lambda},$

( 12.34)

где $\mu = 1/s$ - скорость обслуживания. Заметим, что среднее время пребывания в системе равно среднему времени ожидания для задержанных клиентов (12.17).

Модель восстановления машин (модель Пальма)

Эта модель принадлежит классу циклических систем организации очереди и соответствует чистой системе с ожиданием с ограниченным числом клиентов (смотрите распределение Энгсета для случая систем с потерями).

Первым в 1933 г. эту модель рассмотрел Гнеденко и в 1934 г. опубликовал статью. Метод стал широко известен, когда в 1947 г. C. Пальм издал статью [80] с теоретическим анализом распределения трудовых ресурсов,

Плотность распределения для распределения времени ожидания при дисциплинах организации очереди FCFS, LCFS1 и SIRO (случайная). Во всех трех случаях среднее время ожидания для задержанных вызовов - 5 единиц времени. Коэффициент формы - 2 для FCFS, 3.33 - для LCFS и 10 - для SIRO. Число обслуживающих приборов - 10, и предложенная нагрузка - 8 Эрл. Среднее время обслуживания s = 10 единиц времени.

Рис. 12.4. Плотность распределения для распределения времени ожидания при дисциплинах организации очереди FCFS, LCFS1 и SIRO (случайная). Во всех трех случаях среднее время ожидания для задержанных вызовов - 5 единиц времени. Коэффициент формы - 2 для FCFS, 3.33 - для LCFS и 10 - для SIRO. Число обслуживающих приборов - 10, и предложенная нагрузка - 8 Эрл. Среднее время обслуживания s = 10 единиц времени.

обслуживающих автоматы. Множество машин, которые обычно работают автоматически, обслуживается n ремонтниками. Машины могут сломаться, и тогда понадобится ремонтник, чтобы запустить их в работу снова. Проблема состоит в том, чтобы определить число ремонтников в зависимости от числа машин так, чтобы общие стоимости были минимизированы (по-другому это называется "оптимизированная прибыль"). Машины могут быть, например, текстильными машинами, которые останавливаются, когда заканчивается нить; ремонтники тогда должны заменить пустую бобину машины полной.

Эту модель восстановления машин, или модель взаимного влияния машин, рассматривал Feller (1950 [27] ). Модель соответствует организации очереди в простой закрытой сети и успешно применяется, чтобы решить технические проблемы нагрузки в компьютерных системах. В системе обозначений Кендалла (Лекция 13) система организации очереди обозначается 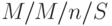M/M/n/S , где - число клиентов и - число обслуживающих приборов.

Модель широко применяется на практике. В сети машины соответствуют вызовам, тогда как "ремонтники" предстают обслуживающими приборами, а "ремонтник" представляется компьютером, управляющим терминалами. В компьютерной си стеме машина может соответствовать программам, хранящимся на диске, а ремонтники представляют каналы ввода-вывода ( ввод-вывод ). Далее мы рассмотрим систему компьютерных терминалов, как основу для развития теории.

Система оконечных устройств

Режим разделения времени - лучшее решение для оптимального обслуживания большой группы источников нагрузки использующих, например, терминалы, подключенные к универсальному компьютеру. Отдельный пользователь должен чувствовать себя так, как будто он - единственный пользователь компьютера (рис.12.5).

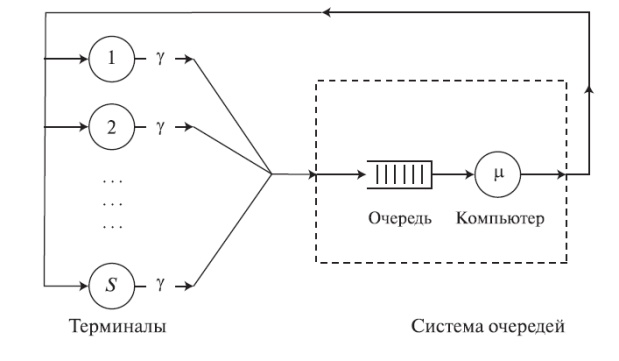
Модель восстановления машин Пальма. Компьютерная система с S терминалами (диалоговая система) соответствует системе с ожиданием и с ограниченным числом источников (см. случай Энгсета для систем с потерями).

Рис. 12.5. Модель восстановления машин Пальма. Компьютерная система с S терминалами (диалоговая система) соответствует системе с ожиданием и с ограниченным числом источников (см. случай Энгсета для систем с потерями).

Отдельный терминал находится все время в одном из двух состояний (диалоговый режим) (рис.12.6):

пользователь думает (работает), или
пользователь ждет ответа от компьютера. Временной интервал, когда пользователь думает, является случайной

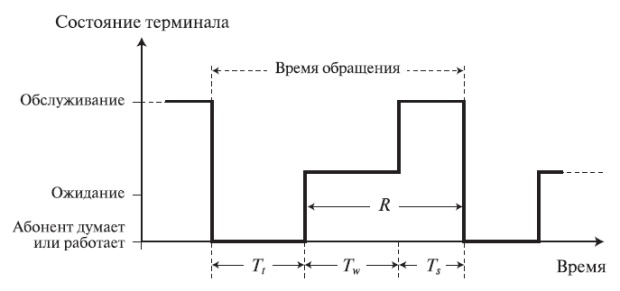
Отдельный терминал может быть в трех различных состояниях. Любой пользователь может работать активно на терминале (или думать), или он ждет ответа от компьютера. Последний временной интервал (время реакции) разделен на две фазы: фаза ожидания и фаза обслуживания.

Рис. 12.6. Отдельный терминал может быть в трех различных состояниях. Любой пользователь может работать активно на терминале (или думать), или он ждет ответа от компьютера. Последний временной интервал (время реакции) разделен на две фазы: фаза ожидания и фаза обслуживания.

Временной интервал, когда пользователь думает, является случайной переменная 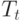T_t со средней величиной m_t. Временной интервал, когда пользователь ждет ответа от компьютера, называется временем реакции R. Он включает в себя временной интервал T_w (средняя величина m_w ), в котором работа ждет получения доступа к компьютеру, и непосредственно время обслуживания T_s (средняя величина m_s ).

T_t +R называются временем обращения (рис.12.6). В конце этого временного интервала терминал возвращается к тому же самому состоянию, т.е. к левой стороне в начале интервала (текущее событие). Далее нас интересуют, главным образом, средние величины и характеристики, которые справедливы для всех дисциплин организации очереди, не нарушающих нормальную работу (секция 13.4.2).

Вероятности состояния одного обслуживающего прибора

Рассмотрим теперь систему с терминалами, которые связаны с одним компьютером. Предполагается, что времена размышления абонента для каждого терминала экспоненциально распределены с интенсивностью $\gamma = 1/m_t$ и время обслуживания (выполнение компьютером работы) распределено экспоненциально с интенсивностью $\mu = 1/m_s$ . Когда есть очередь в компьютере, терминалы должны ждать обслуживания. Обслуживаемые терминалы или ждущие в очереди имеют нулевую интенсивность поступления.

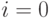Состояние [i] определено как состояние, где в системе организации очереди (рис.12.5) есть терминалов, то есть компьютер либо свободен ( i = 0 ), либо работает ( 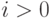i > 0 ), и ( 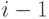i - 1 ) терминалов ждут все время, пока ( i > 0 ).

Система организации очереди может быть смоделирована процессом "гибели и размножения" и диаграммой перехода состояний, показанной на рис.12.7. Существует статистическое равновесие (эргодическая система). Интенсивности поступления заявок уменьшается, по мере того как длина очереди увеличивается, и интенсивность становится нулевой, когда все терминалы стоят в очереди.

Диаграмма переходов для системы организации очереди, показанной в 12.5. Состояние [ i ] обозначает число терминалов, которые либо обслуживаются, либо ожидают обслуживания, то есть S- i обозначает число терминалов, где пользователь либо размышляет, либо работает непосредственно с компьютером.

Рис. 12.7. Диаграмма переходов для системы организации очереди, показанной в 12.5. Состояние [ i ] обозначает число терминалов, которые либо обслуживаются, либо ожидают обслуживания, то есть S- i обозначает число терминалов, где пользователь либо размышляет, либо работает непосредственно с компьютером.

Устойчивые вероятности состояния могут быть найдены, по рис.12.7, с помощью уравнения сечения и выражены с помощью числа состояний :

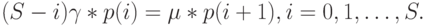$(S-i) \gamma *p(i)= \mu *p(i+1), i=0,1, \dots, S.$

( 12.35)

Согласно дополнительным ограничением нормировки, подставляя $\varrho = \mu / \gamma$ , находим сумму всех вероятностей, которая равна:

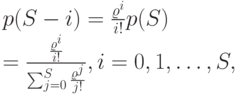$p(S-i)=\frac{\varrho^i}{i!}p(S)\\ =\frac{\frac{\varrho^i}{i!}}{\sum_{j=0}^S \frac{\varrho^j}{j!}}, i=0,1,\dots, S,$

( 12.36)

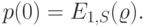$p(0)=E_{1,S}(\varrho).$

( 12.37)

Это - усеченное Пуассоновское распределение (7.9).

Мы можем интерпретировать систему следующим образом. Группе с пучками каналов (терминалами) поступают вызовы от компьютера с экспоненциально распределенными интервалами поступления (интенсивность) $\mu$ .

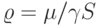Когда все пучков каналов заняты (пауза на размышление или ввод), компьютер свободен, и интенсивность поступления нулевая, но мы могли бы предположить, что все пучки еще генерируют вызовы с интенсивностью $\mu$ , которые потеряны в этой или другой группе пучков каналов (экспоненциальное распределение не имеет памяти). Компьютер, таким образом, предлагает нагрузку $\varrho =\mu / \gamma S$ пучкам каналов, и мы имеем формулу (12.37). B-формула Эрланга справедлива для произвольных времен пребывания в системе (секция 7.3.3), и поэтому можно утверждать, что:

Теорема 12.1. Вероятности состояния модели восстановления машин (12.36) и (12.37) с одним компьютером и терминалами справедливы в течение произвольных времен пауз (размышления и работа с компьютером), когда времена обслуживания компьютером являются экспоненциально распределенными.

Отношение 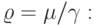$\varrho=\mu / \gamma:$ это отношение среднего времени, когда пользователь терминала думает $1/ \gamma$ , и среднего времени, когда компьютер обслуживает терминал $1/ \mu$ . Это отношение называется сервисным отношением. В B-формуле Эрланга сервисное отношение соответствует предложенной нагрузке. Вероятности состояния определяются числом терминалов и сервисного отношения. Вычисление по формулам (12.36) и (12.37) проводится, как и в B-формуле (7.29) Эрланга.

Пример 12.5.1: Информационная система

Мы рассматриваем информационную систему, которая организована следующим образом. Вся информация хранится на 6 дисках, которые связаны с одним и тем же терминалом мультиплексорным каналом ввода-вывода данных. Среднее время поиска (определение месторасположения производится вручную) - 3 мс. Среднее время задержки, чтобы определить местонахождение файла - 1 мс, соответствующее время вращения - 2 мс, время считывания файла - экспоненциально распределенное со средней величиной 0,8 мс, дисковое хранение основано на определении месторасположения путем считывания при вращении диска так, чтобы канал был занят только в период чтения. Мы хотим найти максимальную производительность системы (число запросов в секунду). Время паузы на раздумье и работу с терминалом 4 мс, и время обслуживания - 0,8 мс, сервисное отношение, таким образом, равно 5.

B-формула Эрланга дает значение:

$1-p(0)=1-E_{1,6}(5)=0.8082.$

Это соответствует $\gamma_{Maкc.}=0.8082/0.0008=1010$ запросов в секунду.

Дальше >>

Авторизоваться

Разработка телетрафика и планирование сетей

Системы с ожиданием