|
мне задали дистанционное задание на сертификат,но я не могу его найти |
Вычисление оптимальных стратегий в бесконечных играх
Игры на единичном квадрате с выбором момента времени
Другим важным классом игр на единичном квадрате, для которых можно найти решение, являются игры с выбором момента времени. В этих играх чистой стратегией каждого игрока является выбор момента времени для выполнения определенных действий. Например в военном деле к таким действиям относится применение оружия каждым из противников друг против друга. Поэтому такие ситуации называются дуэльными или просто дуэлями . Характерной особенностью дуэли является то, что каждый из противников стремится по возможности задержать свой выстрел, так как вероятность поражения с течением времени увеличивается. Однако задержка в применении своего оружия имеет разумные пределы, обусловленные тем, что противник может применить свое оружие раньше и выиграть дуэль.
Примером дуэльных ситуаций в военном деле могут служить бои подводных лодок, истребителей, танков и так далее. В этих ситуациях выбор момента применения оружия каждым из противников после взаимного обнаружения представляет собой стратегию игрока. Немедленное или слишком раннее применение оружия может привести к промаху из-за большой дистанции и отсутствия информации об элементах движения противника, а длительное маневрирование для сближения, определения координат и элементов движения противника даст возможность ему применить свое оружие первым и достичь успеха.
Дуэльная ситуация хорошо моделируется антагонистической бесконечной игрой на единичном квадрате, если считать, что стратегиями игроков являются числа ![x,y \in [0,1]](/sites/default/files/tex_cache/8ccc5717da3dd0b073cc7bf160912733.png) , которые можно интерпретировать как нормированные моменты времени применения оружия каждым из игроков.
, которые можно интерпретировать как нормированные моменты времени применения оружия каждым из игроков.
Функция выигрыша в ситуации  такой игры представляет вероятности поражения игроком I игрока II и определяется следующим соотношением:
такой игры представляет вероятности поражения игроком I игрока II и определяется следующим соотношением:
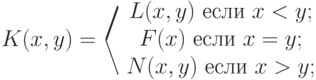 |
( 10.10) |
где 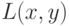 — вероятность поражения игроком I игрока II, если игрок I упреждает игрока II в применении оружия;
— вероятность поражения игроком I игрока II, если игрок I упреждает игрока II в применении оружия;
 — вероятность поражения игроком I игрока II, если оба игрока применяют оружие одновременно;
— вероятность поражения игроком I игрока II, если оба игрока применяют оружие одновременно;
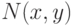 — вероятность поражения игроком I игрока II, если игрок II упреждает игрока I в применении оружия.
— вероятность поражения игроком I игрока II, если игрок II упреждает игрока I в применении оружия.
При задании функции выигрыша принимается, что если игрок II предполагает применить свое оружие в некоторый фиксированный момент времени  , то игрок I
, то игрок I
увеличивает свой выигрыш, выжидая сколько возможно, но действуя все же раньше игрока II. Если же игрок I применяет свое оружие после применения игроком II, то он может проиграть при условии, что оружие игрока II достигает цели. В случае же промаха игрока II шансы на успех у игрока I возрастают со временем. Математически это выражается тем, что функции 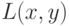 и
и 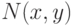 монотонно убывают по
монотонно убывают по  для каждого
для каждого  .
.
Игры с выбором момента времени не обязательно включают по одному действию с каждой стороны, они могут содержать и повторные действия. Кроме того, как и во всех играх, противники могут иметь различную информацию о действиях каждого из них. Решение подобных игр представляет большую сложность, и поэтому рассмотрим только простейший класс, когда каждый из двух противников располагает одним выстрелом, при котором вероятность поражения монотонно возрастает со временем. Кроме того, в этом классе игр действия каждого из игроков, а также их последствия немедленно становятся известными противнику. Поэтому такую игру можно назвать игрой с выбором момента времени в условиях полной информации. Так называемые шумные дуэли являются примером игр этого класса.
В шумной дуэли каждой из двух игроков имеет возможность произвести только один выстрел. По звуку (шуму) каждый игрок знает, что его противник выстрелил. Наличие информации о действиях противника дает возможность считать, что математическое ожидание выигрыша 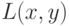 , является функцией только
, является функцией только  , а
, а 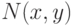 , — функцией только
, — функцией только  .
.
Пусть вероятность поражения  игрока II является непрерывной функцией, которая монотонно возрастает по
игрока II является непрерывной функцией, которая монотонно возрастает по  . Аналогично вероятность поражения
. Аналогично вероятность поражения  игрока I также является непрерывной функцией, которая монотонно возрастает по
игрока I также является непрерывной функцией, которая монотонно возрастает по  .
.
Будем считать, что если игрок I поражает игрока II, то выигрыш игрока I
равен 1; если игрок II поражает игрока I, то выигрыш игрока I равен –1; если ни один из игроков не поражен или поражены оба игрока, то выигрыш игрока I равен 0.
В общем виде математическое ожидание выигрыша игрока I, когда игроки используют чистые стратегии  и
и  , равно (10.10.)
, равно (10.10.)
Определим  следующим образом. При
следующим образом. При  первым применяет оружие игрок I, и вероятность того, что он поразит игрока II, равна
первым применяет оружие игрок I, и вероятность того, что он поразит игрока II, равна  , и выигрыш игрока I будет равна
, и выигрыш игрока I будет равна 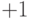 . В случае промаха, вероятность которого равна
. В случае промаха, вероятность которого равна 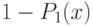 , игрок II применит свое оружие в момент
, игрок II применит свое оружие в момент 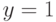 и поразит игрока I, выигрыш которого тогда будет равен –1. Следовательно,
и поразит игрока I, выигрыш которого тогда будет равен –1. Следовательно,
![L(x,y)=P_1(x)+(-1)[1-P_1(x)]=2P_1(x)-1.\\
F(x,y)=P_1(x)+(-1)[1-P_2(x)][1-P_1(x)]=P_1(x)-P_2(x).\\
N(x,y)=(-1)P_2(y)+[1-P_2(y)]=1-2P_2(y)-1](/sites/default/files/tex_cache/81fe0586d895bbcabb57baaed7f81705.png) .
.
Таким образом, математическое ожидание выигрыша игрока в рассматриваемой игре с выбором момента времени будет
 |
( 10.11) |
На основании того, что  и
и  увеличиваются с увеличением
увеличиваются с увеличением  и
и  соответственно, можно записать:
соответственно, можно записать:
![\mathop{max}\limits_x \mathop{min}\limits_y K(x,y) = \mathop{max}\limits_x \mathop{min}\limits_y [2P_1(x)-1,P_1(x)-P_2,1-2P_2(x)]](/sites/default/files/tex_cache/1c1c8198d9fa6bc46f465d058e870102.png)
Для x, которые удовлетворяют неравенству
 |
( 10.12) |
Действительно, на основании 9.12. запишем:
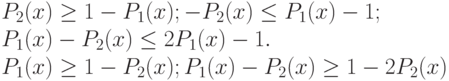 .
.
Следовательно,
 .
.
Для  , которые удовлетворяют равенству
, которые удовлетворяют равенству
![P_1(x)+P_2(x)=1\\ min[2P_1(x)-1,P_1(x)-P_2(x),1-2P_2(x)]=P_1(x)-P_2(x)](/sites/default/files/tex_cache/b2c99e6737e71cd757547b6d6768947b.png) |
( 10.13) |
так как на основании 9.13.
 .
.
Для  , которые удовлетворяют неравенству
, которые удовлетворяют неравенству
![P_1(x)+P_2(x)\le 1,\\ min[2P_1(x)-1,P_1(x)-P_2(x),1-2P_2(x)]=1P_1(x)-1](/sites/default/files/tex_cache/e8b405f185157a736b7bd41276cc0fa5.png) |
( 10.14) |
так как на основании 9.14.
 .
.
Пусть 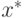 определяется уравнением
определяется уравнением
 .
.
Отсюда
![\mathop{max}\limits_x \mathop{min}\limits_y [2P_1(x)-1,P_1(x)-P_2(x).1-2P_2(x)]=P_1(x^*)1P_2(x^*)](/sites/default/files/tex_cache/9567c689c57daab391cc7aa0be41ca13.png) .
.
Следовательно,
 ,
,
где 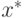 удовлетворяет уравнению
удовлетворяет уравнению
 |
( 10.15) |
Аналогично можно показать, что
 ,
,
где 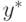 удовлетворяет уравнению
удовлетворяет уравнению
 |
( 10.16) |
Следовательно, функция выигрыша  имеет седловую точку (
имеет седловую точку (  . Отсюда игрок I имеет чистую оптимальную стратегию
. Отсюда игрок I имеет чистую оптимальную стратегию 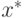 , определяемую из уравнения (10.15.) , игрок II — чистую оптимальную стратегию
, определяемую из уравнения (10.15.) , игрок II — чистую оптимальную стратегию 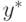 , определяемую из уравнения (10.16.), а значение игры равно
, определяемую из уравнения (10.16.), а значение игры равно
 |
( 10.17) |
Таким образом, пара  является решением игры с выбором момента времени и выражает равновесие между желанием задержки и опасностью промедления.
является решением игры с выбором момента времени и выражает равновесие между желанием задержки и опасностью промедления.
