|
мне задали дистанционное задание на сертификат,но я не могу его найти |
Вычисление оптимальных стратегий в бесконечных играх
Свойства оптимальных стратегий
Математическое ожидание выигрыша игрока I, применяющего чистую стратегию против оптимальной смешанной стратегии игрока II, не может быть больше значения игры.
Математическое ожидание выигрыша игрока I, применяющего оптимальную смешанную стратегию против чистой стратегии игрока II, не может быть меньше значения игры.
У каждого игрока имеется по меньшей мере одна чистая стратегия, применение которой против оптимальной стратегии другого игрока дает математическое ожидание выигрыша, равное значению игры.
Вычисление оптимальных смешанных стратегий в играх на единичном квадрате
Одним из классов игр на единичном квадрате, для которых можно найти решение, являются игры с выпуклыми или вогнутыми функциями выигрыша.
Функция  называется выпуклой по
называется выпуклой по  на интервале
на интервале ![[0,1]](/sites/default/files/tex_cache/ccfcd347d0bf65dc77afe01a3306a96b.png) , если
, если
![K[\lambda u_1 + (1-\lambda)u_2]\le \lambda K(u_1) +(1-\lambda)K(u_2);\\ (u_1,u_2\in u;0 \le \lambda\le 1)](/sites/default/files/tex_cache/9e7aaf0edcfbf779325359d15ec8301b.png) |
( 10.5) |
График такой функции всегда проходит не выше отрезка прямой, проведенной между двумя его точками.
Если в выражении 9.5. имеет место строгое неравенство при  и
и  , то функция
, то функция  называется строго выпуклой. График строго выпуклой функции всегда проходит ниже отрезка прямой, проведенной между любыми его точками. (См. рисунок (10.2).)
называется строго выпуклой. График строго выпуклой функции всегда проходит ниже отрезка прямой, проведенной между любыми его точками. (См. рисунок (10.2).)
В некотором смысле обратным понятию выпуклости является понятие вогнутости.
Функция  называется вогнутой по
называется вогнутой по  на интервале
на интервале ![[0,1]](/sites/default/files/tex_cache/ccfcd347d0bf65dc77afe01a3306a96b.png) , если
, если
![K[\lambda u_1 + (1-\lambda)u_2]\ge \lambda K(u_1) +(1-\lambda)K(u_2);\\ (u_1,u_2\in u;0 \le \lambda\le 1)](/sites/default/files/tex_cache/71213ac4faed5efd00be69fcb94d222f.png) |
( 10.6) |
Если в выражении 9.6. имеет место строгое неравенство при  и
и 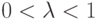 , то функция
, то функция  называется строго вогнутой. График такой функции всегда проходит выше отрезка прямой, проведенной между любыми его точками (рис. 10.3).
называется строго вогнутой. График такой функции всегда проходит выше отрезка прямой, проведенной между любыми его точками (рис. 10.3).
Свойство выпуклости или строгой выпуклости функции выигрыша  по
по  для любого
для любого  устанавливается путем вычисления ее вторых производных по
устанавливается путем вычисления ее вторых производных по  (если они существуют):
(если они существуют):
при  функция
функция  является выпуклой по
является выпуклой по  ;
;
при  функция
функция  является строго выпуклой по
является строго выпуклой по  .
.
Допустим, что функция выигрыша  при любом является строго выпуклой по
при любом является строго выпуклой по  и что игра имеет решение
и что игра имеет решение  .
.
Предположим, что игрок I выбирает число  из интервала
из интервала ![[0,1]](/sites/default/files/tex_cache/ccfcd347d0bf65dc77afe01a3306a96b.png) согласно функции распределения
согласно функции распределения 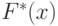 . Тогда для любой чистой стратегии
. Тогда для любой чистой стратегии  игрока II
игрока II
математическое ожидание выигрыша  будет равно
будет равно
 .
.
Функция  является строго выпуклой , так как
является строго выпуклой , так как

Поэтому  принимает минимальное значение в одной точке. Следовательно, оптимальной стратегией игрока II является чистая стратегия
принимает минимальное значение в одной точке. Следовательно, оптимальной стратегией игрока II является чистая стратегия 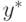 , при которой достигается минимум функции
, при которой достигается минимум функции  . Такую стратегию можно задать одноступенчатой функцией распределения
. Такую стратегию можно задать одноступенчатой функцией распределения

Значение игры в этом случае равно
 ,
,
а константа 
есть решение уравнения
 .
.
Аналогично для функции выигрыша  , строго вогнутой по
, строго вогнутой по  для любого
для любого  , игрок I имеет единственную оптимальную стратегию, являющуюся одноступенчатой функцией
, игрок I имеет единственную оптимальную стратегию, являющуюся одноступенчатой функцией  . Значение игры
. Значение игры  в этом случае равно
в этом случае равно
 ,
,
а константа 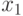 есть решение уравнения
есть решение уравнения
 .
.
Заметим, что свойство вогнутости или строгой вогнутости функции выигрыша  по
по  для любого
для любого  устанавливается путем вычисления ее вторых производных по
устанавливается путем вычисления ее вторых производных по  , если они существуют:
, если они существуют:
при  функция
функция  является вогнутой по
является вогнутой по  ;
;
при  функция
функция  является строго вогнутой по
является строго вогнутой по  .
.
Оптимальные смешанные стратегии игрока I, если функция выигрыша  строго выпукла по
строго выпукла по  , и игрока II, если функция выигрыша
, и игрока II, если функция выигрыша  строго вогнута по
строго вогнута по  , определяются на основании следующих теорем ( доказательство которых дается в Мак-Кенси Д. Введение в теорию игр. М. , Изд-во физико-математической литературы, 1960.).
, определяются на основании следующих теорем ( доказательство которых дается в Мак-Кенси Д. Введение в теорию игр. М. , Изд-во физико-математической литературы, 1960.).
Т е о р е м а 1. Пусть  — функция выигрыша бесконечной игры на единичном квадрате, непрерывная по двум по двум переменным и строго выпуклая по
— функция выигрыша бесконечной игры на единичном квадрате, непрерывная по двум по двум переменным и строго выпуклая по  для любого
для любого  . Пусть
. Пусть 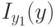 — единственная оптимальная стратегия игрока II, и
— единственная оптимальная стратегия игрока II, и  — значение игры. Если
— значение игры. Если  или
или  , то у игрока I имеется оптимальная стратегия
, то у игрока I имеется оптимальная стратегия 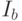 , где константой b может быть любое число, удовлетворяющее условиям:
, где константой b может быть любое число, удовлетворяющее условиям:


Если  , то у игрока I имеется оптимальная стратегия следующего вида:
, то у игрока I имеется оптимальная стратегия следующего вида:
 |
( 10.6) |
где  и
и  — любые числа, удовлетворяющие условиям:
— любые числа, удовлетворяющие условиям:
 |
( 10.7) |
Т е о р е м а 2. Пусть  — функция выигрыша бесконечной игры на единичном квадрате, непрерывная по двум по двум переменным и строго вогнутая по
— функция выигрыша бесконечной игры на единичном квадрате, непрерывная по двум по двум переменным и строго вогнутая по  для любого
для любого  . Пусть
. Пусть  — единственная оптимальная стратегия игрока I, и
— единственная оптимальная стратегия игрока I, и  — значение игры. Если
— значение игры. Если  или
или 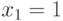 , то у игрока II имеется оптимальная стратегия
, то у игрока II имеется оптимальная стратегия  , где константой b может быть любое число, удовлетворяющее условиям:
, где константой b может быть любое число, удовлетворяющее условиям:


Если  , то
, то  игрока II имеется оптимальная стратегия следующего вида:
игрока II имеется оптимальная стратегия следующего вида:
 |
( 10.8) |
где  и
и 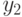 — любые числа, удовлетворяющие условиям:
— любые числа, удовлетворяющие условиям:
 |
( 10.9) |
Из теорем 1 и 2 вытекает, что оптимальная стратегия игрока I для функции выигрыша, строго выпуклой по  , есть чистая стратегия, представляющая одну из точек интервала
, есть чистая стратегия, представляющая одну из точек интервала ![[0,1]](/sites/default/files/tex_cache/ccfcd347d0bf65dc77afe01a3306a96b.png) , если
, если  или 1. Если
или 1. Если  , то оптимальная стратегия игрока I состоит в случайном выборе одного из двух значений
, то оптимальная стратегия игрока I состоит в случайном выборе одного из двух значений  по закону двухступенчатой функции распределения вида 9.6. Для функции выигрыша, строго вогнутой по
по закону двухступенчатой функции распределения вида 9.6. Для функции выигрыша, строго вогнутой по  , оптимальная стратегия игрока II есть чистая стратегия, представляющая одну из точек интервала [0,1], если
, оптимальная стратегия игрока II есть чистая стратегия, представляющая одну из точек интервала [0,1], если 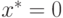 или
или  . Если
. Если  , то оптимальная стратегия игрока II
, то оптимальная стратегия игрока II
Состоит в случайном выборе одного из двух значений  по закону двухступенчатой функции вида (10.8.)
по закону двухступенчатой функции вида (10.8.)
Реализация смешанной стратегии вида (10.6) или (10.8.) заключается в том, что с помощью случайного механизма выбирается число  из интервала
из интервала ![[0,1]](/sites/default/files/tex_cache/ccfcd347d0bf65dc77afe01a3306a96b.png) и
и  принимает значение
принимает значение  , если
, если  и
и  , если
, если  .
.
Решение игры на единичном квадрате с выпуклой (вогнутой) функцией выигрыша можно найти аналогично решению игры, функция выигрыша которой является строго выпуклой (вогнутой). Однако в этом случае оптимальная стратегия игрока I, указанная в теореме 9.2. (или игрока I в теореме 9.1.), вообще уже не является единственной.




