|
мне задали дистанционное задание на сертификат,но я не могу его найти |
Метод вычисления оптимальных стратегий
Вычисление оптимальных стратегий в биматричных играх
Описание биматричной игры. Все игры которые были рассмотрены, относились к классу игр с нулевой суммой. Однако ряд конфликтных ситуаций, складывающихся в ходе действий, характерны тем, что выигрыш одной стороны не равен в точности проигрышу другой. Теоретико-игровыми моделями подобных ситуаций являются некооперативные игры с ненулевой суммой. Такие игры называются биматричными, потому что задание каждой такой игры сводится к заданию двух матриц  и
и  одинаковой формы:
одинаковой формы:  .
.
Процесс биматричной игры состоит в независимом выборе игроком I числа  а игроком II — числа
а игроком II — числа  , после чего игрок I получает выигрыш
, после чего игрок I получает выигрыш 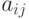 , а игрок II — выигрыш
, а игрок II — выигрыш  .
.
Номера строк матриц  и
и  назовем чистыми стратегиями игрока I, а номера столбцов этих матриц – чистыми стратегиями игрока II. Тогда пары вида
назовем чистыми стратегиями игрока I, а номера столбцов этих матриц – чистыми стратегиями игрока II. Тогда пары вида 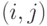 будут являться ситуациями в чистых стратегиях биматричной игры, а числа
будут являться ситуациями в чистых стратегиях биматричной игры, а числа 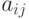 и
и  — выигрышами I и II игроков в ситуации
— выигрышами I и II игроков в ситуации 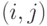 . Соответственно, распределение вероятностей применения чистых стратегий игрока I —
. Соответственно, распределение вероятностей применения чистых стратегий игрока I —  и игрока II —
и игрока II —  будем называть смешанными стратегиями. Тогда пары вида
будем называть смешанными стратегиями. Тогда пары вида  представляют ситуации биматричной игры в смешанных стратегиях, а числа
представляют ситуации биматричной игры в смешанных стратегиях, а числа  и
и  являются математическими ожиданиями выигрыша I и II игроков.
являются математическими ожиданиями выигрыша I и II игроков.
Ситуацией равновесия биматричной игры в смешанных стратегиях будем называть такую пару  , при которой:
, при которой:
 |
( 8.2) |
где  — математическое ожидание выигрыша игрока I;
— математическое ожидание выигрыша игрока I;
 — математическое ожидание выигрыша игрока II;
— математическое ожидание выигрыша игрока II;
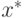 — оптимальная смешанная стратегия игрока I;
— оптимальная смешанная стратегия игрока I;
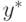 — оптимальная смешанная стратегия игрока II.
— оптимальная смешанная стратегия игрока II.
Задача
Построение и решение биматричной игры. Предположим, что противолодочная подводная лодка страны  осуществляет поиск ракетной подводной лодки государства
осуществляет поиск ракетной подводной лодки государства  , которая маневрирует в строго определенной части района боевого патрулирования. В остальной части этого района действует противолодочная подводная лодка
, которая маневрирует в строго определенной части района боевого патрулирования. В остальной части этого района действует противолодочная подводная лодка  , которая осуществляет поиск противолодочной подводной лодки
, которая осуществляет поиск противолодочной подводной лодки  . Пусть каждая противолодочная лодка для обнаружения противника может использовать свою гидроакустическую станцию или в активном режиме, включая ее периодически, или только в пассивном режиме, выполняя непрерывный поиск.
. Пусть каждая противолодочная лодка для обнаружения противника может использовать свою гидроакустическую станцию или в активном режиме, включая ее периодически, или только в пассивном режиме, выполняя непрерывный поиск.
Как противолодочная подводная лодка  , так и ракетная подводная лодка
, так и ракетная подводная лодка  с обнаружением сигналов гидролокатора может уклониться от противника. Однако периодичность включения гидролокатора делает обнаружение возможным, но недостоверным.
с обнаружением сигналов гидролокатора может уклониться от противника. Однако периодичность включения гидролокатора делает обнаружение возможным, но недостоверным.
В подобной конфликтной ситуации одним из игроков является противолодочная подводная лодка  , а другим — противолодочная подводная лодка
, а другим — противолодочная подводная лодка  .Очевидно, ракетная подводная лодка не может быть игроком, так как она имеет только один способ действий, заключающийся в скрытом маневрировании и выполнении уклонения с обнаружением сигналов гидролокаторов.
.Очевидно, ракетная подводная лодка не может быть игроком, так как она имеет только один способ действий, заключающийся в скрытом маневрировании и выполнении уклонения с обнаружением сигналов гидролокаторов.
Характерным здесь является то, что каждый из игроков преследует разные, но не противоположные цели. Действительно, целью противолодочной подводной лодки  является обнаружение ракетной подводной лодки, а целью противолодочной подводной лодки
является обнаружение ракетной подводной лодки, а целью противолодочной подводной лодки  — обнаружение противолодочной подводной лодки
— обнаружение противолодочной подводной лодки  . Поэтому для оценки достижения цели каждым из игроков в зависимости от выбранных способов действий (стратегий) необходимо иметь два критерия эффективности и соответственно две функции выигрыша. Тогда моделью подобной конфликтной ситуации будет конечная игра с ненулевой суммой, описываемая двумя матрицами одинаковой формы
. Поэтому для оценки достижения цели каждым из игроков в зависимости от выбранных способов действий (стратегий) необходимо иметь два критерия эффективности и соответственно две функции выигрыша. Тогда моделью подобной конфликтной ситуации будет конечная игра с ненулевой суммой, описываемая двумя матрицами одинаковой формы 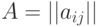 и
и  , называемая биматричной.
, называемая биматричной.
Примем за критерий эффективности противолодочной подводной лодки  (игрок I ) вероятность обнаружения ракетной подводной лодки
(игрок I ) вероятность обнаружения ракетной подводной лодки  , а за критерий эффективности противолодочной подводной лодки
, а за критерий эффективности противолодочной подводной лодки  (игрок II ) – вероятность обнаружения противолодочной подводной лодки
(игрок II ) – вероятность обнаружения противолодочной подводной лодки 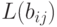 . Тогда биматричная игра будет задана матрицей
. Тогда биматричная игра будет задана матрицей  (рисунок 9.a) и матрицей
(рисунок 9.a) и матрицей  (рисунок 9.b).
(рисунок 9.b).
Где  — использование активного режима;
— использование активного режима;
 — использование пассивного режима.
— использование пассивного режима.
Для решения полученной биматричной игры  достаточно задать значения вероятностей
достаточно задать значения вероятностей 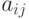 и
и  .
.
Пусть для конкретных значений вероятностей 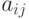 и
и  биматричная игра задана матрицами
биматричная игра задана матрицами  (рис. 8.c) и
(рис. 8.c) и  (рис. 8.d).
(рис. 8.d).
Из анализа матриц  и
и  устанавливаем, что
устанавливаем, что  и
и 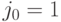 , то есть игроки осуществляют ситуацию равновесия в чистых стратегиях, так как максимальные элементы матриц
, то есть игроки осуществляют ситуацию равновесия в чистых стратегиях, так как максимальные элементы матриц  и
и  принадлежат паре
принадлежат паре 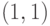 .
.
Таким образом, моделью конфликтной ситуации, в которой противники преследуют разные, но не прямо противоположные цели, является биматричная игра. Ее особенность по сравнению с матричной игрой заключается в наличии двух матриц, элементы каждой из которых равны значениям критерия эффективности соответствующего игрока. Принцип оптимальности, лежащий в основе вычислительной процедуры смешанных стратегий, исходит из обеспечения игрокам выигрыша, которой остается неизменным и равным значению игры независимо от действий противника.




