НОУ ИНТУИТ | Основы математического моделирования. Лекция 7: Прикладные задачи дискретного программирования

Учитесь и получайте официальные документы БЕСПЛАТНО. Вы можете поддержать наш проект.

Регистрация Вход

Твой путь к знаниям!

Новосибирский Государственный Университет

Опубликован: 06.11.2008 | Доступ: свободный | Студентов: 3338 / 1210 | Оценка: 4.24 / 3.67 | Длительность: 14:37:00

Темы: Математика, Образование

Специальности: Математик

|

Вам нравится? Нравится 41 студенту

| Поделиться |

Поддержать курс

| Скачать электронную книгу

Аннотация: Задачи планирования перевозок. Задача размещения и специализации. Задачи логического проектирования. Задача теории расписаний. Задача о наилучшем распределении памяти вычислительной машины. Задача финансирования исследовательских проектов. Задача из области экономики сельского хозяйства.

Задачи планирования перевозок

Простейшей и наиболее популярной задачей планирования перевозок является транспортная задача, которую мы разобрали в "шестой лекции" .

Широкий класс дискретных моделей возникает при формулировке задач о перевозках, связанных с использованием неделимых транспортных единиц. К изучению некоторых моделей такого рода сейчас мы и переходим.

Рассмотрим распределительную задачу. Эта математическая модель широко освещалась в литературе под самыми различными названиями (обобщенная транспортная задача, задача о взвешенном распределении, $\lambda$ -задача, задача о расстановке флота и др.). Опишем ее в следующей интерпретации.

Обобщенная транспортная задача, задача о взвешенном распределении, $\lambda$ -задача, задача о расстановке флота и др.

Пусть имеется транспортных линий (скажем, пассажирских); по -й линии нужно выполнить b_j рейсов (j=1,2,...,n) . В наличии имеются транспортные единицы m типов. Резервы полезного времени транспортной единицы типа составляют a_i (i=1,2,...,m) . На выполнение транспортной единицей типа рейса требуется время $t_{ij}$ , а затраты на рейс составляют $c_{ij}$ . Требуется указать наиболее экономную расстановку транспортных единиц по линиям.

Обозначая через $x_{ij}$ количество рейсов, которое транспортная единица должна выполнить по линии , приходим к следующей задаче. Требуется минимизировать

$\sum\limits_{i=1}^{m} \sum\limits_{j=1}^{n} c_{ij} x_{ij}$

( 7.1)

при условиях

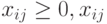$x_{ij}\ge 0, x_{ij}$

( 7.2)

- целые,

,

$\sum\limits_{j=1}^{n} t_{ij} x_{ij}\le a_i, i=1,2,...,m$

( 7.3)

,

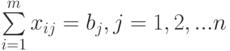$\sum\limits_{i=1}^{m} x_{ij} =b_j, j=1,2,...n$

( 7.4)

.

Здесь условия (7.3.) выражают ограничения по фондам времени каждой транспортной единицы, а условия (7.4.) говорят о том, что все рейсы должны быть выполнены.

К совершенно аналогичной модели приводит близкая к описанной задача о выборе средства доставки груза.

Задача о выборе средства доставки груза.

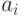Пусть через i=1,2,...,m обозначены грузообразующие пункты с объемами груза в них a_i . Имеется средств доставки груза (видов транспорта); грузоподъемность - го средства доставки составляет p_j , а наличный его парк равен N_j, j=1,2,...n . Грузы подлежат доставке в один центральный пункт (склад); затраты при осуществлении одной единицей средства доставки рейса от пункта до склада равны $c_{ij}$ . Требуется составить наиболее экономный план доставки.

Через $x_{ij}$ обозначим количество средств доставки типа , отправляющееся из пункта . Тогда задача сведется к минимизации целевой функции вида (7.1.) при условиях (7.2.) и

$\sum\limits_{j=1}^{n} p_jx_{ij} \ge a_i, i=1,2,...,m$

( 7.5)

,

$\sum\limits_{i=1}^{m} x_{ij}=N_j, j=1,2,...n$

( 7.6)

.

Распределительная задача имеет весьма разнообразные приложения. Большое число практических ее интерпретаций можно найти в монографии Д.Б. Юдина и Е.Г. Гольштейна (Юдин Д.Б., Гольштейн Е.Г., Задачи и методы линейного программирования . Изд. 2-е переработанное и дополненное, М., "Советское радио", 1964.)

Задача распределения производственной программы.

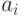Пусть требуется распределить изготовление деталей между станками. Индексом j=1,2,...,n будем обозначать детали, индексом i=1,2,...,m — станки с резервами рабочего времени a_i . Пусть плановое задание по деталям задается числами b_j , штучные нормы времени по обработке -м станком -й детали равны $t_{ij}$ , а себестоимость при этом составляет $c_{ij}$ . Требуется составить план распределения работ по станкам, обеспечивающий выполнение задания, не выводящий за пределы резервов времени по каждому станку и минимизирующий суммарную себестоимость.

Обозначим через $x_{ij}$ количество деталей типа , которое следует обработать на станке . Тогда описанная задача распределения программы сведется к модели (7.1.)-(7.4.). Заметим, что во многих интерпретациях распределительной задачи требование целочисленности на переменные может и не накладываться.

Распределительная задача с фиксированными доплатами.

Пусть в дополнение к перечисленным выше данным выпуск транспортной единицы типа на линию связан с подготовительными работами, требующими времени $\tau_{ij}$ (это время не зависит от числа рейсов, которое предстоит выполнить данной транспортной единице). Денежные затраты на проведение этих подготовительных работ составляют $d_{ij}$ .

Для отыскания наиболее экономной расстановки транспортных единиц по линиям, как и выше, введем целочисленные переменные $x_{ij}$ . Тогда суммарные затраты составят

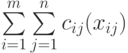$\sum\limits_{i=1}^{m}\sum\limits_{j=1}^{n}c_{ij}(x_{ij})$

( 7.7)

,

где

$c_{ij}(x_{ij})= \left\langle \begin{array}{ccc} 0, x_{ij},\\ c_{ij}x_{ij}+d_{ij}, x_{ij} > 0 \end{array} \right$

( 7.8)

Ограничения по фонду времени каждой транспортной единицы будут теперь иметь вид

$\sum\limits_{i=1}^{n}t_{ij}(x_{ij})\le a_i, i=1,2,...,m$

( 7.9)

,

где

$t_{ij}(x_{ij})= \left\langle \begin{array}{ccc} 0, x_{ij}=0,\\ t_{ij}x_{ij}+\tau_{ij}, x_{ij} > 0 \end{array} \right$

( 7.10)

Ограничения по рейсам (7.4.), равно как и очевидные ограничения (7.2.), при этом сохраняются. Таким образом, задача заключается в минимизации (7.7.) при условиях (7.2.), (7.4.) и (7.9.)

Из (7.7.) и (7.8.) легко усмотреть, что перед нами задача с фиксированными доплатами; ее отличие от рассматривавшихся ранее задач этого рода состоит в том, что здесь фиксированные доплаты входят не только в целевую функцию, но и в ограничения (7.9.). Однако и этот вариант задачи можно свести к целочисленная задача линейного программирования.

Задача о выборе средств доставки грузов.

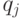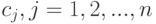Пусть грузовой флот имеет в своем составе суда типов. Количество судов типа равно q_j , а затраты при использовании одного судна типа в планируемом периоде составляют c_j, j=1,2,...,n . Каждое судно обладает грузовыми емкостями типов (трюмы, танки, палубы и тому подобное); грузоподъемность емкости на судне типа равна $d_{ij}$ . Подлежат перевозке видов грузов. Груз вида имеется в количестве a_k, k=1,2,...,p . Требуется выбрать наиболее экономичный комплекс средств доставки этих грузов, совместимый с грузовыми возможностями судов.

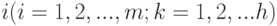Учитывая неделимость транспортных единиц, введем целочисленные переменные x_j, j=1,2,...,n , которые обозначают количество судов типа , выделяемое для перевозки. Кроме того, введем переменные $y_{ik}$ , которые обозначают количество грузов вида , подлежащее загрузке в емкость i(i=1,2,...,m;k=1,2,...h) . Тогда мы придем к задаче минимизации

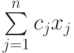$\sum\limits_{j=1}^{n}c_jx_j$

( 7.11)

при условиях

$0\le x_j\le q_j, x_j$

( 7.12)

- целое; $y_{ik}\ge 0$ ,

$\sum\limits_{j=1}^{n}d_{ij}x_j-\sum\limits_{k=1}^{p}y_{ik}\ge 0, i=1,2,...,m$

( 7.13)

,

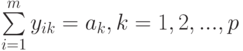$\sum\limits_{i=1}^{m}y_{ik}=a_k, k=1,2,...,p$

( 7.14)

.

Здесь ограничения (7.13.) показывают, что общее количество груза, загружаемое в емкости каждого типа, не должно превышать суммарной грузоподъемности этих емкостей по всем судам, а ограничения (7.14.) говорят о том, что перевозки по всем грузам должны быть полностью осуществлены. Отметим, что на переменные $y_{ik}$ требование целочисленности, вообще говоря, не накладывается, так что здесь мы имеем дело с частично целочисленной задачей.

Дальше >>

Авторизоваться

Основы математического моделирования

Прикладные задачи дискретного программирования

Задачи планирования перевозок

Задача о выборе средства доставки груза.

Задача распределения производственной программы.

Распределительная задача с фиксированными доплатами.

Задача о выборе средств доставки грузов.

Вопросы и ответы