|
Подскажите, пожалуйста, планируете ли вы возобновление программ высшего образования? Если да, есть ли какие-то примерные сроки? Спасибо! |
Типовые математические модели
2.7. Принцип квазирегулярности
Как показывает практика, метод динамики средних вполне приемлем и для немарковских процессов, то есть для произвольных распределений времен нахождения элементов в состояниях 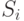 .
.
Хотя в этих случаях мы формально не имеем права написать уравнения динамики средних, однако массовость явления делает вид распределения не очень существенным. Следовательно, при моделировании не следует тратить время на проверку марковости процесса. Чем больше элементов в системе, чем она сложнее, тем точнее она моделируется методом динамики средних.
При большом числе элементов также становится не очень существенным требование однородности элементов.
Теперь попробуем разобраться с требованием, которое мы также ввели ранее - требование независимости элементов.
Применяя метод динамики средних, мы можем встретиться с очень серьезной трудностью. Дело в том, что интенсивности потоков событий, переводящих элементы из одного состояния в другое, могут зависеть от численности состояний. Например, в примере 2.6 интенсивность  зависит от того, сколько в данный момент времени находится СС в состоянии
зависит от того, сколько в данный момент времени находится СС в состоянии  : СС может либо сразу ремонтироваться, либо ожидать очереди ввиду занятости рабочих мест. Численности состояний случайны, следовательно, интенсивности потоков событий тоже случайны и неизвестны. Точное решение в таких ситуациях невозможно, однако вполне приемлемое для практики решение находится с помощью допущения, которое называют "принцип квазирегулярности".
: СС может либо сразу ремонтироваться, либо ожидать очереди ввиду занятости рабочих мест. Численности состояний случайны, следовательно, интенсивности потоков событий тоже случайны и неизвестны. Точное решение в таких ситуациях невозможно, однако вполне приемлемое для практики решение находится с помощью допущения, которое называют "принцип квазирегулярности".
Принцип квазирегулярности состоит в следующем: интенсивности  зависят не от мгновенных значений численности состояний
зависят не от мгновенных значений численности состояний  , а от их средних значений (математических ожиданий)
, а от их средних значений (математических ожиданий)  .
.
Погрешность от этого допущения при моделировании тем меньше, чем ближе к линейной зависимости 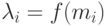 и чем больше общее количество элементов
и чем больше общее количество элементов  .
.
На практике проверено, что при 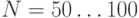 точность моделирования приемлема для инженерных "прикидок", если же функции
точность моделирования приемлема для инженерных "прикидок", если же функции 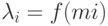 близки к линейным, то приемлемые результаты получаются и при
близки к линейным, то приемлемые результаты получаются и при  .
.
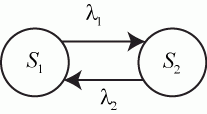
Пример 2.9. Каждый автомат, находящийся на вооружении в воинской части, может находиться в исправном состоянии или ремонтироваться в мастерской части. Если бы каждый неисправный автомат сразу попадал к свободному мастеру, то никаких очередей из автоматов, ожидающих ремонта, не было, и граф состояний автомата имел бы вид, приведенный на рис. 2.17.
Здесь:
 - автомат неисправен, ремонтируется;
- автомат неисправен, ремонтируется;
 - интенсивность выхода автомата из строя;
- интенсивность выхода автомата из строя;
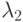 - интенсивность ремонта автомата одним мастером.
- интенсивность ремонта автомата одним мастером.
В этом случае  и
и 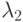 были бы постоянными величинами и, естественно, не зависели от численности состояний. Уравнения динамики средних имели бы вид:
были бы постоянными величинами и, естественно, не зависели от численности состояний. Уравнения динамики средних имели бы вид:
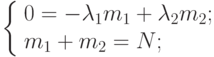
так как мы полагаем, что процессы наработки на отказ и ремонта - марковские и стационарный режим существует.  - общее число автоматов в части.
- общее число автоматов в части.
Уравнение для состояния  не пишем, так как оно линейно зависит от первого.
не пишем, так как оно линейно зависит от первого.
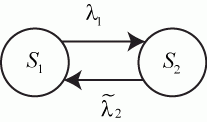
А теперь предположим, что в мастерской части два мастера и неисправные автоматы могут ожидать ремонта. В этом случае интенсивность переходов из неисправного состояние в исправное зависит от числа автоматов, находящихся в мастерской. Обозначим эту интенсивность  . Граф состояний имеет вид (рис. 2.18).
. Граф состояний имеет вид (рис. 2.18).
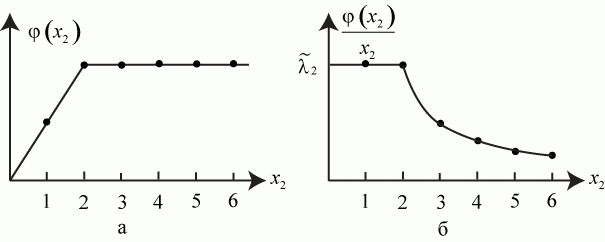
Общую интенсивность ремонта мастерской обозначим 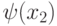 . График ее показан на рис. 2.19а.
. График ее показан на рис. 2.19а.
При 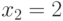 интенсивность
интенсивность 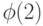 максимальна, так как работают оба мастера. При дальнейшем увеличении
максимальна, так как работают оба мастера. При дальнейшем увеличении 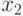 интенсивность
интенсивность 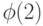 возрастать не может.
возрастать не может.
Очевидно, интенсивность ремонта, приходящаяся на один автомат, находящийся в мастерской:
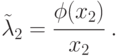
График зависимости  от
от  показан на рис. 2.19б.
показан на рис. 2.19б.
Применим принцип квазирегулярности, то есть будем считать, что  зависит не от случайных численностей
зависит не от случайных численностей  , а от среднего значения (матожидания)
, а от среднего значения (матожидания)  . Тогда:
. Тогда:
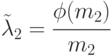
и уравнения динамики средних примут вид:
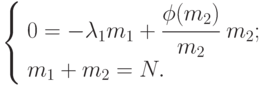
Зависимость 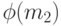 задана рис. 2.19б.
задана рис. 2.19б.
Пример 2.10. Вернемся к задаче о пеленгации передатчиков противника. Поскольку целью ее решения являлось определение среднего числа запеленгованных передатчиков, то возможно применение метода динамики средних. Обозначим:
 - состояние "передатчик запеленгован";
- состояние "передатчик запеленгован";
 - случайная численность состояния
- случайная численность состояния  ;
;
 - состояние "передатчик потерян";
- состояние "передатчик потерян";
 - интенсивность обнаружения частоты передатчика противника одним оператором;
- интенсивность обнаружения частоты передатчика противника одним оператором;
 - интенсивность потерь слежения запеленгованного передатчика противника;
- интенсивность потерь слежения запеленгованного передатчика противника;
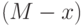 - текущее число операторов, ведущих поиск;
- текущее число операторов, ведущих поиск;
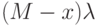 - интенсивность обнаружения всеми операторами одного передатчика;
- интенсивность обнаружения всеми операторами одного передатчика;
 - число не захваченных частот передатчиков, находящихся в состоянии
- число не захваченных частот передатчиков, находящихся в состоянии  .
.
Граф состояний одного передатчика приведен на рис. 2.20. Заменим, в соответствии с принципом квазирегулярности, случайную численность обнаруженных передатчиков  на среднее значение
на среднее значение  и, учитывая наличие стационарности, запишем уравнение динамики средних:
и, учитывая наличие стационарности, запишем уравнение динамики средних:
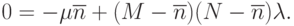
Уравнения динамики средних могут быть нелинейными и, следовательно, решение будет не единственным. В таких случаях берется то решение, которое не противоречит смыслу задачи.
Для упрощения расчетов положим 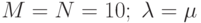 . В этом случае уравнение принимает вид:
. В этом случае уравнение принимает вид:
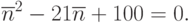
Его решение 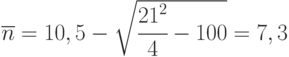 передатчика (знак плюс перед корнем отбрасываем, так как в этом случае корень будет равен 13,7, что бессмысленно). Решение этого примера с помощью уравнений Колмогорова дает ответ
передатчика (знак плюс перед корнем отбрасываем, так как в этом случае корень будет равен 13,7, что бессмысленно). Решение этого примера с помощью уравнений Колмогорова дает ответ 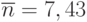 . Расхождение в 2,5 % объясняется малочисленностью группировок
. Расхождение в 2,5 % объясняется малочисленностью группировок  и
и  . Впрочем, полученный результат может быть вполне приемлемым.
. Впрочем, полученный результат может быть вполне приемлемым.