|
Добрый день. Я приступила сегодня к самостоятельному изучению курса "Моделирование систем". Хочу понять - необходимо ли отсылать мои решения практических заданий на сайт, (и если да - то где найти волшебную кнопку "Загрузить...") или практические задания остаются полностью на моей совести? (никто не проверяет, и отчётности по ним я предоставлять не обязана?) P.S.: тьютора я не брала |
Исследование качества генераторов случайных чисел
1.4. Исследование качества ГСЧ, сформированного по линейному конгруэнтному методу
Формирование случайных (псевдослучайных) чисел по линейному конгруэнтному методу основывается на следующем рекуррентном соотношении:
 |
( 5.1) |
где:
 — вновь формируемое число;
— вновь формируемое число;
 — множитель (мультипликативная константа);
— множитель (мультипликативная константа);
 — предыдущее число (
— предыдущее число (  — назначаемое число);
— назначаемое число);
 — приращение (инкремент);
— приращение (инкремент);
 — модуль, бинарная операция для обозначения остатка от деления двух чисел;
— модуль, бинарная операция для обозначения остатка от деления двух чисел;
 — целочисленная константа [19]. Для
— целочисленная константа [19]. Для  -разрядных целых чисел
-разрядных целых чисел  . В самом простом случае принимается, что
. В самом простом случае принимается, что 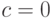 Массив случайных чисел
Массив случайных чисел  из интервала
из интервала  будет формироваться следующим образом:
будет формироваться следующим образом:
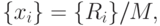 |
( 5.2) |
где 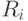 — числа, определяемые по формуле (5.1).
— числа, определяемые по формуле (5.1).
В стандартной процедуре реализации линейного конгруэнтного метода (5.1) принимается, что  — целые положительные числа. Приведем определение конгруэнтности двух чисел
— целые положительные числа. Приведем определение конгруэнтности двух чисел  и
и  : два числа
: два числа  и
и  конгруэнтны (сравнимы) по модулю числа
конгруэнтны (сравнимы) по модулю числа  , если они дают одинаковые остатки при делении на этот модуль
, если они дают одинаковые остатки при делении на этот модуль  . Таким образом, по формуле (5.1) число
. Таким образом, по формуле (5.1) число  будет конгруэнтно по модулю
будет конгруэнтно по модулю  числу
числу  .
.
При выборе чисел  придерживаются следующих правил:
придерживаются следующих правил:
-
 — должны быть взаимно простыми числами. Причем число
— должны быть взаимно простыми числами. Причем число  определяет собой период числовой псевдослучайной последовательности: чем больше
определяет собой период числовой псевдослучайной последовательности: чем больше  , тем длиннее последовательность псевдослучайных чисел;
, тем длиннее последовательность псевдослучайных чисел; -
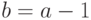 кратно
кратно  для любого простого
для любого простого  , являющегося делителем
, являющегося делителем  .
.
В качестве множителя  рекомендуется принимать первообразный корень по модулю
рекомендуется принимать первообразный корень по модулю  . Приведем следующее классическое определение.
. Приведем следующее классическое определение.
Первообразный корень по модулю  — натуральное число
— натуральное число 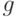 , такое, что наименьшее положительное число
, такое, что наименьшее положительное число  , для которого разность
, для которого разность  делится на
делится на  (без остатка), совпадает с
(без остатка), совпадает с  , где
, где  — число натуральных чисел, меньших
— число натуральных чисел, меньших  и взаимно простых с
и взаимно простых с  .
.
Например, при  первообразным корнем по модулю 7 является число 3. Действительно,
первообразным корнем по модулю 7 является число 3. Действительно,  , т. е. количеству чисел ряда
, т. е. количеству чисел ряда  , каждое из которых взаимно просто с числом 7.
, каждое из которых взаимно просто с числом 7.
Два числа называются взаимно простыми, если в качестве общего делителя они имеют только единицу.
Числа  не делятся на 7 без остатка, и лишь
не делятся на 7 без остатка, и лишь  делится на 7 (частное от деления равно 104).
делится на 7 (частное от деления равно 104).
В системе MATLAB формирование простых чисел производится с помощью функции  (см.
(см.  ). Для проверки, являются ли два числа взаимно простыми, можно применить функцию
). Для проверки, являются ли два числа взаимно простыми, можно применить функцию  , которая определяет наибольший общий делитель для двух чисел.
, которая определяет наибольший общий делитель для двух чисел.
В самом простом случае принимается, что 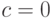 При этом можно использовать следующие рекомендации по выбору параметров генератора:
При этом можно использовать следующие рекомендации по выбору параметров генератора:
- Начальное значение
 может быть произвольно.
может быть произвольно. - Выбор
 должен удовлетворять трем требованиям:
должен удовлетворять трем требованиям:  ,
,  двоичные знаки
двоичные знаки  не должны иметь очевидного шаблона.
не должны иметь очевидного шаблона. - В качестве
 следует выбирать нечетное число, такое, что
следует выбирать нечетное число, такое, что
Пример формирования модуля  в командном окне MATLAB:
в командном окне MATLAB:
>> N = 7*10^6;
>> m = primes(N);
>> M = m(end)
M =
6999997Задание 4
- Полагая в формуле (5.1)
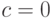 , напишите в MATLAB программу формирования случайных чисел, приняв следующие числа
, напишите в MATLAB программу формирования случайных чисел, приняв следующие числа  для расчета модуля в зависимости от номера варианта:
для расчета модуля в зависимости от номера варианта:
- В качестве первого назначаемого случайного числа
 (в зависимости от номера варианта) примите следующие значения:
(в зависимости от номера варианта) примите следующие значения:№ 1 № 1:  , № 2:
, № 2:  , № 3:
, № 3:  , № 4:
, № 4: 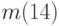 , № 5:
, № 5:  , № 6:
, № 6: 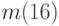 , № 7:
, № 7:  , № 8:
, № 8:  , № 9:
, № 9:  , где
, где  — массив простых чисел, сформированный с помощью выражения
— массив простых чисел, сформированный с помощью выражения 
№ 2 № 1: 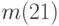 , № 2:
, № 2: 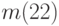 , № 3:
, № 3:  , № 4:
, № 4:  , № 5:
, № 5:  , № 6:
, № 6:  , № 7:
, № 7:  , № 8:
, № 8:  , № 9:
, № 9:  , где
, где  — массив простых чисел, сформированный с помощью выражения
— массив простых чисел, сформированный с помощью выражения 
№ 3 № 1:  , № 2:
, № 2:  , № 3:
, № 3:  , № 4:
, № 4:  , № 5:
, № 5:  , № 6:
, № 6:  , № 7:
, № 7:  , № 8:
, № 8:  , № 9:
, № 9:  , где
, где  — массив простых чисел, сформированный с помощью выражения
— массив простых чисел, сформированный с помощью выражения 
№ 4 № 1:  , № 2:
, № 2: 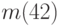 , № 3:
, № 3:  , № 4:
, № 4:  , № 5:
, № 5:  , № 6:
, № 6:  , № 7:
, № 7:  , № 8:
, № 8:  , № 9:
, № 9:  , где
, где  — массив простых чисел, сформированный с помощью выражения
— массив простых чисел, сформированный с помощью выражения 
- Вычислите период формируемой случайной последовательности (с помощью функции
 ).
). - Произведите статистический анализ созданного ГСЧ по линейному конгруэнтному методу.
- Постройте гистограммы полученных распределений случайных чисел с помощью функции
 .
. - Постройте функции плотности и распределения для сформированных выборок случайных чисел. Совместите диаграммы с теоретическими функциями.
2. Статистическое тестирование выборки псевдослучайных чисел по критерию Колмогорова–Смирнова
По критерию Колмогорова–Смирнова (КС-критерию) осуществляется проверка простой статистической гипотезы  (нулевой гипотезы) о том, что функция распределения
(нулевой гипотезы) о том, что функция распределения  случайной величины
случайной величины  совпадает с некоторой известной функцией
совпадает с некоторой известной функцией  при некотором уровне значимости
при некотором уровне значимости  . КС-критерием можно пользоваться уже при объеме выборки
. КС-критерием можно пользоваться уже при объеме выборки  .
.
В системе MATLAB КС-критерий реализован функцией  .
.
Рассмотрим пример использования функции  для проверки гипотезы о том, что функция распределения
для проверки гипотезы о том, что функция распределения 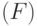 выборки, сформированной с помощью функции
выборки, сформированной с помощью функции  , соответствует функции распределения
, соответствует функции распределения  экспоненциального закона с параметром 1 той же самой выборки.
экспоненциального закона с параметром 1 той же самой выборки.
Программное решение примера в командном окне MATLAB:
>> x = rand(25,1); F0 = expcdf(x,1);
>> H = kstest(x,[x,F0])
H =
1Полученный результат  означает, что нулевая гипотеза отвергается, т. е. выборочная функция равномерного распределения
означает, что нулевая гипотеза отвергается, т. е. выборочная функция равномерного распределения 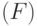 в интервале
в интервале ![[0; 1]](/sites/default/files/tex_cache/f083648758df2ddf9560f0b17ac28d3b.png) имеет значительные расхождения с предполагаемой функцией экспоненциального распределения
имеет значительные расхождения с предполагаемой функцией экспоненциального распределения  с уровнем значимости
с уровнем значимости  = 0.05 (по умолчанию). Если закладывается другой уровень значимости, отличный от 0.05, то тогда он должен быть введен в функцию
= 0.05 (по умолчанию). Если закладывается другой уровень значимости, отличный от 0.05, то тогда он должен быть введен в функцию  . На том же примере это будет выглядеть так (с уровнем значимости 0.012):
. На том же примере это будет выглядеть так (с уровнем значимости 0.012):
>> x = rand(25,1); F0 = expcdf(x,1);
>> H = kstest(x,[x,F0],0.012)
H =
1По-прежнему нулевая гипотеза отвергается.
Рассмотрим пример использования функции  для проверки гипотезы о том, что функция распределения выборки, сформированной с помощью
для проверки гипотезы о том, что функция распределения выборки, сформированной с помощью  , соответствует функции распределения равномерного закона из интервала
, соответствует функции распределения равномерного закона из интервала ![[0; 1]](/sites/default/files/tex_cache/f083648758df2ddf9560f0b17ac28d3b.png) той же самой выборки.
той же самой выборки.
Решение примера в командном окне MATLAB:
>> x = rand(25,1); F0 = unifcdf(x,0,1);
>> H = kstest(x,[x,F0])
H =
0Нулевая гипотеза о равномерном распределении выборки принимается.
Задание 5
- По критерию Колмогорова–Смирнова протестируйте выборки случайных чисел, сформированных по методу срединных квадратов.
- По критерию Колмогорова–Смирнова протестируйте выборки случайных чисел объема 100, 500, 1000, сформированных по линейному конгруэнтному методу.

 № 2:
№ 2: 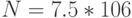 ; № 3:
; № 3: 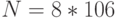 ; № 4:
; № 4:  ; № 5:
; № 5:  ; № 6:
; № 6:  ; № 7:
; № 7:  ; № 8:
; № 8: 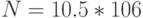 ; № 9:
; № 9: 
 ; № 2:
; № 2:  ; № 3:
; № 3: 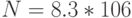 ; № 4:
; № 4:  ; № 5:
; № 5:  ; № 6:
; № 6:  ; № 7:
; № 7: 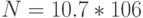 ; № 8:
; № 8:  ; № 9:
; № 9: 
 ; № 2:
; № 2:  ; № 3:
; № 3: 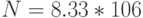 ; № 4:
; № 4:  ; № 5:
; № 5:  ; № 8:
; № 8:  ; № 9:
; № 9: 
 ; № 2:
; № 2:  ; № 3:
; № 3: 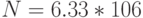 ; № 4:
; № 4: 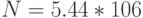 ; № 5:
; № 5:  ; № 6:
; № 6:  ; № 7:
; № 7:  ; № 8:
; № 8:  ; № 9:
; № 9: 