Контрастирование (редукция) нейронной сети
Рекурсивное контрастирование и бинаризация
Рекурсивное контрастирование состоит в модификации параметров системы -
одного за другим. Для этого параметры должны быть как-то линейно
упорядочены  . При модификации
. При модификации 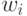 используются модифицированные
значения
используются модифицированные
значения 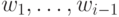 и немодифицированные
и немодифицированные  .
.
Пусть для сумматора задана обучающая выборка входных векторов  и
соответствующих выходных сигналов
и
соответствующих выходных сигналов  , а также известны
значения
параметров, которые реализуют сумматор:
, а также известны
значения
параметров, которые реализуют сумматор: 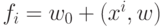 .
Требуется
произвести бинаризацию сумматора, т.е. найти числа
.
Требуется
произвести бинаризацию сумматора, т.е. найти числа  и вектор
и вектор 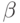 с
координатами
с
координатами  или
или  , чтобы значения функции
, чтобы значения функции 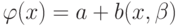 на выборке
на выборке 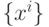 как можно меньше отличались от
как можно меньше отличались от  .
Критерием такого отличия будем
считать
.
Критерием такого отличия будем
считать 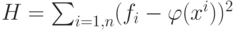 . Построим
координаты вектора
. Построим
координаты вектора 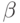 по порядку
по порядку  .
.
Пусть построены  .
Обозначим
.
Обозначим  (последние
(последние 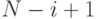 координат - нули),
координат - нули),  (последние
(последние 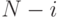 координат - нули),
координат - нули),  (первые
(первые  координат - нули).
координат - нули).
Введем функции:
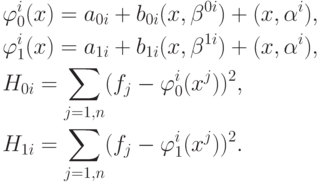
Определим параметры 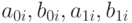 из условий
из условий  , минимизируя функции
, минимизируя функции  и
и  .
Пусть
.
Пусть  и
и 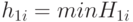 .
Если
.
Если 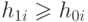 , то полагаем
, то полагаем  , в противном случае
, в противном случае  .
.
После того как построены все 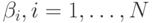 (
(  - размерность вектора
данных), автоматически определяются
- размерность вектора
данных), автоматически определяются  и
и  : если
: если  , то полагаем
, то полагаем  ,
, 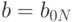 , иначе
, иначе 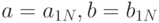 .
.
Если бинаризация проведена, а необходимая точность не достигнута, то можно
построить второй бинаризованный сумматор, корректирующий ошибку первого ---
так, чтобы в сумме они хорошо аппроксимировали работу исходного сумматора
на элементах обучающей выборки. В описанной процедуре делаем замену  и для этих исходных данных вновь строим
бинаризованный сумматор
по алгоритму рекурсивной бинаризации. Повторяем такое построение, пока не
будет достигнута удовлетворительная точность. В результате получим набор
бинаризованных сумматоров, которые в совокупности (т.е. в результате
суммирования выходных сигналов) достаточно точно аппроксимируют исходный.
При появлении весов, определяющих значимость отдельных примеров из
обучающей выборки, рекурсивная бинаризация проводится точно так же,
только в функциях
и для этих исходных данных вновь строим
бинаризованный сумматор
по алгоритму рекурсивной бинаризации. Повторяем такое построение, пока не
будет достигнута удовлетворительная точность. В результате получим набор
бинаризованных сумматоров, которые в совокупности (т.е. в результате
суммирования выходных сигналов) достаточно точно аппроксимируют исходный.
При появлении весов, определяющих значимость отдельных примеров из
обучающей выборки, рекурсивная бинаризация проводится точно так же,
только в функциях 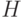 появляются веса.
появляются веса.
Если требуется тем же путем упростить любой другой элемент, линейный по
параметрам,  , то вместо обучающей
выборки
, то вместо обучающей
выборки  берем
семейство векторов
берем
семейство векторов 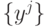 с координатами
с координатами  . После такого
. После такого  преобразования рассматриваемый элемент превращается в обычный сумматор,
для которого последовательность действий уже описана.
преобразования рассматриваемый элемент превращается в обычный сумматор,
для которого последовательность действий уже описана.
