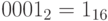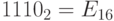|
Не очень понятно про оболочечные Данные,ячейки памяти могут наверно размер менять,какое это значение те же операции только ячейки больше,по скорости тоже самое |
Работа с числами в языке Java
Шестнадцатеричное представление целых чисел и перевод из одной системы счисления в другую
Во время программирования различного рода внешних устройств, регистров процессора, битовыми масками, кодировке цвета, и так далее, приходится работать с кодами беззнаковых целых чисел. При этом использование десятичных чисел крайне неудобно из-за невозможности легкого сопоставления числа в десятичном виде и его двоичных бит. А использование чисел в двоичной кодировке крайне громоздко – получаются слишком длинные последовательности нулей и единиц. Программисты используют компромиссное решение – шестнадцатеричную кодировку чисел, где в качестве основания системы счисления выступает число 16. Очевидно,  . В десятичной системе счисления имеется только 10 цифр: 0,1,2,3,4,5,6,7,8,9. А в 16-ричной системе счисления должно быть 16 цифр. Принято обозначать недостающие цифры заглавными буквами латинского алфавита: A,B,C,D,E,F. То есть
. В десятичной системе счисления имеется только 10 цифр: 0,1,2,3,4,5,6,7,8,9. А в 16-ричной системе счисления должно быть 16 цифр. Принято обозначать недостающие цифры заглавными буквами латинского алфавита: A,B,C,D,E,F. То есть  .
Таким образом, к примеру,
.
Таким образом, к примеру,  .
.
В Java для того, чтобы отличать 16-ричные числа, как мы уже знаем, перед ними ставят префикс 0x: 0xFF обозначает  , а 0x10 – это
, а 0x10 – это  , то есть 16.
, то есть 16.
Число N может быть записано с помощью разных систем счисления. Например, в десятичной:

или в двоичной:

или в шестнадцатеричной:

Преобразование в другую систему счисления сводится к нахождению соответствующих коэффициентов. Например,  по известным коэффициентам
по известным коэффициентам  – при переводе из десятичной системы в двоичную, или коэффициентов
– при переводе из десятичной системы в двоичную, или коэффициентов  по коэффициентам
по коэффициентам  - из двоичной системы в десятичную.
- из двоичной системы в десятичную.
Преобразование чисел из системы с меньшим основанием в систему с большим основанием
Рассмотрим преобразование из двоичной системы в десятичную. Запишем число N в виде

и будем рассматривать как алгебраическое выражение в десятичной системе. Выполним арифметические действия по правилам десятичной системы. Полученный результат даст десятичное представление числа N.
Пример:
Преобразуем  к десятичному виду. Имеем:
к десятичному виду. Имеем:
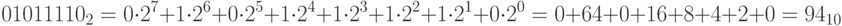
Преобразование чисел из системы с большим основанием в систему с меньшим основанием
Рассмотрим его на примере преобразования из десятичной системы в двоичную. Нужно для известного числа  найти коэффициенты в выражении
найти коэффициенты в выражении

Воспользуемся следующим алгоритмом: в десятичной системе разделим число N на 2 с остатком. Остаток деления (он не превосходит делителя) даст коэффициент 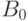 при младшей степени
при младшей степени  . Далее делим на 2 частное, полученное от предыдущего деления. Остаток деления будет следующим коэффициентом
. Далее делим на 2 частное, полученное от предыдущего деления. Остаток деления будет следующим коэффициентом  двоичной записи N. Повторяя эту процедуру до тех пор, пока частное не станет равным нулю, получим последовательность коэффициентов
двоичной записи N. Повторяя эту процедуру до тех пор, пока частное не станет равным нулю, получим последовательность коэффициентов  .
.
Например, преобразуем  к двоичному виду. Имеем:
к двоичному виду. Имеем:
| частное | остаток |  |
|
|---|---|---|---|
| 345 / 2 | 172 | 1 | 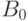 |
| 172 / 2 | 86 | 0 |  |
| 86 / 2 | 43 | 0 |  |
| 43 / 2 | 21 | 1 | 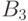 |
| 21 / 2 | 10 | 1 |  |
| 10 / 2 | 5 | 0 |  |
| 5 / 2 | 2 | 1 |  |
| 2 / 2 | 1 | 0 |  |
| 1 / 2 | 0 | 1 |  |

Преобразование чисел в системах счисления с кратными основаниями
Рассмотрим число N в двоичном и шестнадцатеричном представлениях.


Заметим, что 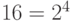 . Объединим цифры в двоичной записи числа группами по четыре. Каждая группа из четырех двоичных цифр представляет число от 0 до
. Объединим цифры в двоичной записи числа группами по четыре. Каждая группа из четырех двоичных цифр представляет число от 0 до  то есть от 0 до
то есть от 0 до  . От группы к группе вес цифры изменяется в
. От группы к группе вес цифры изменяется в  раз (основание 16-ричной системы). Таким образом, перевод чисел из двоичного представления в шестнадцатеричное и обратно осуществляется простой заменой всех групп из четырех двоичных цифр на шестнадцатеричные (по одному на каждую группу) и обратно :
раз (основание 16-ричной системы). Таким образом, перевод чисел из двоичного представления в шестнадцатеричное и обратно осуществляется простой заменой всех групп из четырех двоичных цифр на шестнадцатеричные (по одному на каждую группу) и обратно :
Например, преобразуем  к шестнадцатеричному виду:
к шестнадцатеричному виду: