Национальный исследовательский ядерный университет «МИФИ»
Опубликован: 30.03.2005 | Доступ: свободный | Студентов: 8221 / 2596 | Оценка: 4.17 / 4.05 | Длительность: 09:46:00
ISBN: 978-5-9556-0040-6
Тема: Аппаратное обеспечение
Специальности: Разработчик аппаратуры
Теги:
Лекция 5:
Минимизация неполностью определенных функций
Аннотация: В лекции представлена минимизация неполностью определенных функций, дан синтез функций в базисах штрих Шеффера и стрелка Пирса, даны подходы к минимизации конъюнктивных форм.
Ключевые слова: неполностью определенная функция, функция, СДНФ, импликанта, конституента, импликантная матрица, минимизация, диаграмма Вейча, конфигурация, ранг, СКНФ, КНФ, принцип суперпозиции, стрелка Пирса, операция конъюнкции, суперпозиция, штрих Шеффера, одноэлементный базис
Очень часто, если не в большинстве случаев, работа конкретного устройства описывается с помощью неполностью определенной функции, так как некоторые комбинации входных сигналов не подаются или являются запрещенными.
Определение. Неполностью определенной функцией является такая переключательная функция, значения которой на некоторых наборах аргументов могут быть произвольными (т.е. равными " 0 " или " 1 ").
Определение. Пусть функция f(x1,x2,...xn) не определена на " р " наборах аргументов. Тогда полностью определенную функцию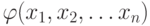 
будем считать эквивалентной к f(x1,x2,...xn), если ее значения на тех наборах, на которых f(x1,x2,...xn) определена, совпадают.
Очевидно, существует 2р различных функций, эквивалентных f(x1,x2,...xn).
Задача минимизации f(x1,x2,...xn) состоит в выборе такой эквивалентной 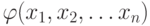, которая имеет простейшую форму.
Введем две вспомогательные эквивалентные функции 
, 
, которые принимают на запрещенных наборах аргументов значения 0 и 1 соответственно.
ТЕОРЕМА. СДНФ неполностью определенной f(x1,x2,...xn) совпадает с дизъюнкцией самых коротких импликант , которые совместно накрывают все конституенты единицы , и ни одна из которых не является лишней.
Пример:
Пусть задана f(x1,x2,...xn) в виде следующей таблицы:
| f(x1,x2,...xn) | 1 | - | - | - | 0 | 1 | 0 | 0 | 1 | 0 | - | 0 | 1 | - | - | 1 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Числовые эквиваленты наборов | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 |
Тогда
,
а
1
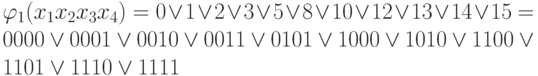
Построим импликантную матрицу.
Конституенты единицы  |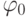
0000 | 0101 | 1000 | 1100 | 1111 |
|---|---|---|---|---|---|
Простые импликанты  | |||||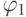
| 0-01 | + | ||||
| -101 | + | ||||
| 110- | + | ||||
| 11-0 | + | ||||
| 00-- | + | ||||
| -0-0 | + | + | |||
| 1--0 | + | + | |||
| 11-- | + | + |
Выполним оптимальное покрытие конституент единицы 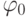простыми импликантами 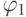и получаем минимальную форму функции f(x1x2 x3 x4)
Минимизация с помощью диаграмм Вейча неполностью определенных функций в наглядной и удобной форме позволяет отыскать минимальные формы.
Пример:
Рассмотрим функцию f(x1x2 x3 x4) и найдем ее минимальную форму. Заполнить диаграмму Вейча по следующим правилам: в клетки диаграммы поставим единицы, которые соответствуют конституентам единицы, нули – для отсутствующих конституент и символ неопределенности – " * " (звездочка) – в остальные.
Видно, что в клетки для конституент: x1x2x3x4, x1x2x3x4, x1x2x3x4 целесообразно "поставить" единицы вместо символов неопределенности, так как в этом случае образуется правильная конфигурация 2-го ранга, которая покрывается произведением x2x3.
Аналогично и в клетку x1x2x3x4 нужно "поставить" единицу.
Итак,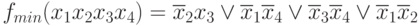 
.
Замечание. Все, что было сказано относительно минимизации функции, представленной в СДНФ или ДНФ справедливо для функции, заданной в СКНФ или КНФ.
В этом случае необходимо отыскивать правильные конфигурации, образованные нулями.
Людмила Долгих
|
Здравствуйте. В первой лекции курса "Логические и арифметические основы и принципы работы ЭВМ" у вас приведена классическая структурная схема ЭВМ. Если можно уточните, а как в классической архитектуре могла реализоваться прямая работа устройств ввода-вывода с оперативной памятью? Если я правильно понимаю - это режим прямого доступа к памяти, в классической архитектуре он не предусмотрен. |