Метод проб
Метод Квайна – Мак – Класки
Основное неудобство метода Квайна состоит в том, что при поиске простых импликант необходимо производить попарные сравнения вначале всех конститутент единицы, затем полученных в результате склеивания произведений.
С целью упрощения этой процедуры Мак – Класки предложил алгоритм, существо которого сводится к следующему:
- вводится понятие цифрового эквивалента для каждого произведения по следующему правилу: некоторому произведению ставится в соответствие цифровой эквивалент с использованием цифр 0 и 1 и – (прочерк). Переменной, входящей в произведение в прямом виде ставится в соответствие единица ( 1 ), в инверсном – нуль ( 0 ), отсутствие переменной обозначается прочерком;
- в любом произведении переменные располагаются только в одном порядке, а именно – по возрастанию индексов;
- склейке подлежат только те произведения, в которых прочерки расположены соответственно, количество нулей (или единиц) отличается на единицу и они расположены так же соответственно.
Пример:
Произведению x1x2x4 для функции, зависящей от пяти переменных нужно поставить в соответствие следующий цифровой набор: x1x2x4: 11-0-
Приведем графическое изображение процесса поиска простых импликант для функции, представленной в следующей СДНФ:
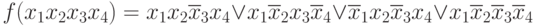
запишем выражение функции в виде дизъюнкции цифровых эквивалентов:
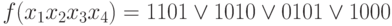
При графическом способе отыскания простых импликант вначале все цифровые наборы разбивают на группы и располагают эти группы в следующем порядке: вначале идет группа цифровых эквивалентов, содержащих только нули (такой набор может быть один), затем следует группа с наборами, содержащими по одной единице, затем по две и т.д. Сравнением наборов соседних групп устанавливается возможность склейки, делается необходимая пометка и пишется результат склейки. Процесс продолжается до тех пор, пока возможны склейки. Все несклеенные наборы, а также конечные результаты склейки дают простые импликанты. Расшифровка полученных цифровых эквивалентов - очевидна.
Для нашего примера это выглядит так:
| Цифровые эквиваленты конституенты единицы | Отметки о склейке | Результат склейки | Отметки о склейке |
|---|---|---|---|
| 1000 | * | 10-0 | - |
| 0101 | * | ||
| 1010 | * | -101 | - |
| 1101 | * |
10-0 и -101, т.е. 
Метод импликантных матриц
Для поиска минимальной формы функции пользуются методом импликантных матриц. Существо метода заключается в следующем: составляется импликантная матрица, колонки которой именуются конституентами единицы, а строки – простыми импликантами. Затем находится минимальное покрытие всех конституент единицы простейшими импликантами. При этом ищется такая минимальная совокупность простых импликант, которые совместно покрывают все конституенты единицы исходной функции. Факт покрытия отмечается в клетке матрицы символом * (звездочка) в случае, когда импликанта покрывает соответствующую конституенту (является ее собственной частью). Из всех простых импликант выбираются вначале только такие, которые только одни покрывают конституенты единицы (в колонке матрицы только один символ покрытия), затем производится перебор.
Пример:
Из матрицы видно, что в минимальную форму функции обязательно войдут импликанты n (покрывает конституенту F ), импликанта r (покрывает конституенту D ). То же справедливо отностительно импликанты p. Что касается остальных, то нужно выбрать минимальную совокупность.
Итак:
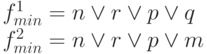
Т.е. данная функция имеет две одинаково минимальные формы.
Замечание: важным обстоятельством, усложняющим минимизацию функций, является присутствие перебора различных вариантов при поиске оптимального покрытия.
