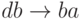Языки логического программирования
[+]
Ярославский Государственный Университет им. П.Г. Демидова
Опубликован: 06.11.2008 | Доступ: свободный | Студентов: 989 / 62 | Оценка: 4.50 / 4.00 | Длительность: 10:47:00
Тема: Программирование
Специальности: Программист, Архитектор программного обеспечения
Теги: nil, алгебра, алгоритмы, анализ, вычисления, законы, книги, кортеж, нормальный алгоритм, подстановка, потоки, предикат, программирование, процедуры, РЕФАЛ, рефал-выражение, рефал-предложение, спецификации, терм, цепочка символов, элементы
Лекция 1:

Нормальные алгоритмы Маркова
A
|
версия для печати
Лекция 1 || Лекция 2 >
Аннотация: Определение нормального алгоритма Маркова и его выполнение. Возможности нормальных алгоритмов Маркова и тезис Маркова. Методика разработки нормальных алгоритмов Маркова.
Ключевые слова: нормальный алгоритм, алгорифм, алгоритм, алгоритмическая, нормальный алгоритм Маркова, НАМ, логическое программирование, алфавит, пустой символ, слово, символ алфавита, подстановки, подстановка, левое слово, правое слово, качество данных, строка символов, Шаг работы алгоритма, строка данных, преобразование данных, правило остановки, входные данные, место, нормальная функция, область определения, входное слово, выходное слово, арифметическая операция, нормальных алгоритмов Маркова, входная строка, специальный символ, Рефал, значение, копирование, вычитание, ветвление, тезис Маркова, определенность алгоритма, методику разработки НАМ, декомпозиция

Определение нормального алгоритма и его выполнение

В середине прошлого века выдающийся русский математик А.А. Марков ввел понятие нормального алгоритма (алгорифма) с целью уточнения понятия "алгоритм", что позволяет решать задачи по определению алгоритмически неразрешимых проблем. Позже это понятие получило название нормального алгоритма Маркова (НАМ). Язык НАМ, с одной стороны, намеренно беден, что необходимо для цели введения понятия "алгоритм". Однако, с другой стороны, идеи НАМ положены в основу большой группы языков программирования, получивших название языки логического программирования, которые являются темой данного пособия.

Для определения НАМ вводится произвольный алфавит - конечное непустое множество символов, при помощи которых описывается алгоритм и данные. В алфавит также включается пустой символ, который мы будем обозначать греческой буквой \lambda. Под словом понимается любая последовательность непустых символов алфавита либо пустой символ, который обозначает пустое слово.

Всякий НАМ определяется конечным упорядоченным множеством пар слов алфавита, называемых подстановками . В паре слов подстановки левое (первое) слово непустое, а правое (второе) слово может быть пустым символом. Для наглядности левое и правое слово разделяются стрелкой. Например,

  1. ab\to bd
  2. db\to ba
  3. bba\to abb
  4. c\to \lambda

В качестве данных алгоритма берется любая непустая строка символов. Работа НАМ состоит из последовательности совершенно однотипных шагов. Шаг работы алгоритма может быть описан следующим образом:

  1. В упорядоченной последовательности подстановок ищем самую первую подстановку, левое слово которой входит в строку данных.
  2. В строке данных ищем самое первое (левое) вхождение левого слова найденной подстановки.
  3. Это вхождение в строке данных заменяем на правое слово найденной подстановки (преобразование данных).

Шаг работы алгоритма повторяется до тех пор, пока

  • либо не возникнет ситуация, когда шаг не сможет быть выполнен из-за того, что ни одна подстановка не подходит ( левое слово любой подстановки уже не входит в строку данных ) - правило остановки ;
  • либо не будет установлено, что процесс подстановок не может остановиться.

В первом случае строка данных, получившаяся при остановке алгоритма, является выходной (результатом) и алгоритм применим к входным данным, а во втором случае алгоритм не применим к входным данным.

Так, определенный выше в примере нормальный алгоритм Маркова преобразует слово 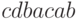cdbacab в слово bbddd следующим образом (над стрелкой преобразования мы пишем номер применяемой подстановки, а в преобразуемой строке подчеркиваем левое слово применяемой подстановки ):

cdbac\underline{ab}\stackrel{1}{\to} c\underline{db}acbd\stackrel{2}{\to} \underline{c}baacbd\stackrel{4}{\to} baa\underline{c}bd\stackrel{4}{\to} ba\underline{ab}d\stackrel{1}{\to} b\underline{ab}dd\stackrel{1}{\to} bbddd,

а при преобразовании слова abbc этот же алгоритм будет неограниченно работать, так как имеет место цикличное повторение данных:

\underline{ab}bc\stackrel{1}{\to} b\underline{db}c\stackrel{2}{\to} \underline{bba}c\stackrel{3}{\to} \underline{ab}bc\stackrel{1}{\to}\dots

Таким образом, всякий нормальный алгоритм Маркова определяет функцию, которую мы назовем нормальной (или вычислимой по Маркову), которая может быть частичной и которая в области определения входному слову ставит в соответствие выходное слово.

Возможности нормальных алгоритмов и тезис Маркова

Прежде всего рассмотрим возможности реализации арифметических операций с помощью нормальных алгоритмов Маркова. Сначала обратим внимание на одно обстоятельство, связанное с работой любого НАМ: нужно либо вводить дополнительное правило остановки работы нормального алгоритма (иначе в примере увеличения числа на 1 алгоритм продолжит работу и снова будет увеличивать полученный результат еще на 1 и т.д. неограниченное число раз), либо перед началом работы нормального алгоритма добавлять к входной строке специальные символы, отличные от других символов строки, которые учитываются подстановками алгоритма в начале его работы и которые удаляются в конце работы алгоритма. Мы будем придерживаться второго способа, как и одна из наиболее успешных реализаций нормальных алгоритмов Маркова в виде языка программирования Рефал. В качестве добавляемого символа возьмем символ "@".

Пример 1. Рассмотрим простейшую операцию увеличения десятичного числа на 1. В этом случае почти всегда необходимо увеличить последнюю цифру на 1, а последняя цифра отличается тем, что после нее идет символ "@". Поэтому первыми подстановками должны быть подстановки типа

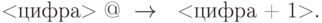
\mbox{<цифра> }@\ \to\ \mbox{ <цифра + 1>}.

Но если это цифра 9, то ее нужно заменить 0 и увеличение на 1 перенести в предыдущий разряд. Этому отвечает подстановка

9@\ \to\ @0.

Наконец, если число начинается с 9 и перед этой цифрой нужно поставить 1, то этому будет отвечать подстановка

@@\ \to\ 1,

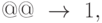
а если это не так, то в конце работы алгоритма символы @ надо стереть, что выполнит подстановка

@\ \to\ \lambda.

Таким образом, мы получаем следующий НАМ увеличения десятичного числа на 1:

1.\text{ } 0@ \to 1 \qquad \ 9.\ 8@\to 9\\ 2.\text{ } 1@ \to 2 \qquad 10.\ 9@ \to @0\\ 3.\text{ } 2@ \to 3 \qquad 11.\ @@ \to 1\\ \text{ } ............... \qquad 12.\ @\to \lambda

Приведем работу построенного алгоритма для чисел 79 и 99:

@7\underline{9@}\stackrel{10}{\to}@\underline{7@}0\stackrel{8}{\to} \underline{@}80\stackrel{12}{\to}80,\\ @9\underline{9@}\stackrel{10}{\to}@\underline{9@}0\stackrel{10}{\to} \underline{@@}00\stackrel{11}{\to}100.

Аналогичным образом разрабатывается нормальный алгоритм Маркова для уменьшения числа на 1 (см. упражнение 1.3.1).

Пример 2. Прежде, чем перейти к другим арифметическим операциям, рассмотрим как довольно типичный пример, используемый часто в других алгоритмах, алгоритм копирования двоичного числа. В этом случае прежде всего исходное и скопированное числа разделим символом "*". В разрабатываемом алгоритме мы будем копировать разряды числа по очереди, начиная с младшего, но нужно решить 2 проблемы: как запоминать значение символа, который мы копируем, и как запоминать место копируемого символа. Для решения второй проблемы используем символ "!", которым мы будем определять еще не скопированный разряд числа, после которого и стоит этот символ. Для запоминания значения копируемого разряда мы будем образовывать для значения 0 символ "a", а для значения 1 - символ "b". Меняя путем подстановок эти символы "a" или "b" с последующими, мы будем передвигать разряды "a" или "b" в начало копируемого числа (после "*"), но для того, чтобы пока не происходило копирование следующего разряда справа, мы перед передвижением разряда временно символ "!" заменим на символ "?", а после передвижения сделаем обратную замену. После того как все число окажется скопированным в виде символов "a" и "b", мы заменим эти символы на 0 и 1 соответственно. В результате нормальный алгоритм копирования двоичного числа можно определить следующей последовательностью подстановок:

\begin{displaymath} \begin{array}{ll} 1.\ 0@\ \to\ 0!*\\ 2.\ 1@\ \to\ 1!*\\ \end{array} \bigg\} \mbox{ начальные пометки копир. разряда и копии числа\qquad\qquad\qquad\qquad\qquad\quad\ } \end{displaymath} \begin{displaymath} \begin{array}{ll} 3.\ 0!\ \to\ ?0a\\ 4.\ 1!\ \to\ ?1b\\ \end{array} \bigg\} \mbox{ копирование разряда с заменой пометки разряда\qquad\qquad\qquad\qquad\qquad\quad\ } \end{displaymath} \begin{displaymath} \begin{array}{ll} 5.\ a0\ \to\ 0a\\ 6.\ a1\ \to\ 1a\\ 7.\ b0\ \to\ 0b\\ 8.\ b1\ \to\ 1b\\ \end{array} \Bigg\} \mbox{\ передвижение скопированного разряда\qquad\qquad\qquad\qquad\qquad\quad\ } \end{displaymath} \begin{displaymath} \begin{array}{ll} 9.\ a*\ \to\ *a\\ 10.\ b*\ \to\ *b\\ \end{array} \bigg\} \mbox{\ остановка передвижения скопированного разряда\qquad\qquad\qquad\qquad\qquad\quad\ } \end{displaymath} \begin{displaymath} \begin{array}{ll} 11.\ ?\ \to\ ! \end{array} \qquad\qquad\mbox{обратная замена пометки разряда\qquad\quad\qquad\qquad\qquad\qquad\qquad}\\ \end{displaymath} \begin{displaymath} \begin{array}{ll} 12.\ a\ \to\ 0\\ 13.\ b\ \to\ 1\\ \end{array} \quad\ \bigg\} \mbox{\ обратная замена скопированного разряда\qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad\quad\ } \end{displaymath} \begin{displaymath} \begin{array}{ll} 14.\ @!\ \to\ \lambda\end{array} \mbox{\qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad\quad} \end{displaymath}

Продемонстрируем работу алгоритма для числа 10:

@1\underline{0@}\stackrel{1}{\to} @1\underline{0!}*\stackrel{3}{\to} @1?0\underline{a*}\stackrel{9}{\to} @1\underline{?}0*a\stackrel{11}{\to} @\underline{1!}0*a\stackrel{4}{\to} @?1\underline{b0}*a\stackrel{7}{\to} @?10\underline{b*}a\stackrel{10}{\to} @\underline{?}10*ba\stackrel{11}{\to} @!10*\underline{b}a\stackrel{13}{\to} @!10*1\underline{0}\stackrel{12}{\to} \underline{@!}10*10\stackrel{14}{\to} 10*10

Для построения алгоритма сложения двух чисел можно использовать идею уменьшения одного числа на 1 с последующим увеличением другого числа на 1 и повторением этого до тех пор, пока уменьшаемое число не исчезнет после того, как станет равным 0. Но можно использовать и более сложную идею поразрядного сложения с переносом 1 в разряд слева. Построение этих алгоритмов, а также алгоритмов вычитания, умножения и деления выделено для самостоятельной работы в упражнениях 2 - 9 (см. 1.3).

Приведенные примеры показывают также возможности аппарата нормальных алгоритмов Маркова по организации ветвления и цикличных процессов вычисления. Это показывает, что всякий алгоритм может быть нормализован т. е. задан нормальным алгоритмом Маркова. В этом и состоит тезис Маркова, который следует понимать как определение алгоритма.

Вместе с тем построение алгоритма в последнем приведенном примере подсказывает следующую методику разработки НАМ:

  1. Произвести декомпозицию (разбиение на части) строящегося алгоритма. В примере это следующие части:
    1. разделение исходного числа и копии;
    2. копирование разряда;
    3. повторение предыдущей части до полного копирования всех разрядов.
  2. Решение проблем реализации каждой части. В примере это следующие проблемы:
    1. запоминание копируемого разряда - разряд 1 запоминается как символ "a", а разряд 0 - как символ "b";
    2. запоминание места копируемого разряда - пометка еще не скопированного символа дополнительным символом "!" с заменой его на символ "?" при передвижении копируемого разряда и обратной заменой после передвижения.
  3. Если часть для реализации является сложной, то она также подвергается декомпозиции.
  4. Сборка реализации в единый алгоритм.

Упражнения

  1. Определите нормальный алгоритм, который уменьшает число на единицу.
  2. Определите нормальный алгоритм сложения двух двоичных чисел методом уменьшения одного числа на 1 и увеличением другого числа на 1 до тех пор, пока уменьшаемое число не станет равным 0.
  3. Определите нормальный алгоритм логического сложения двух двоичных чисел.
  4. Определите нормальный алгоритм логического умножения двух двоичных чисел.
  5. Определите нормальный алгоритм сложения по модулю 2 двух двоичных чисел.
  6. Определите нормальный алгоритм поразрядного сложения двух двоичных чисел.
  7. Определите нормальный алгоритм вычитания двоичных чисел.
  8. Определите нормальный алгоритм умножения двух двоичных чисел столбиком.
  9. Определите нормальный алгоритм деления двух двоичных чисел с определением частного и остатка.
  10. Определите нормальный алгоритм вычисления наибольшего общего делителя двух двоичных чисел.
  11. Определите нормальный алгоритм вычисления наименьшего общего кратного двух двоичных чисел.
Дальше >>
Лекция 1 || Лекция 2 >

Вопросы и ответы

вопросов: 0