Теорема Робертса
Лемма 8.6. Для всех  :
:
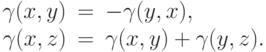
Доказательство. Доказательство проведем в два этапа. Сначала покажем, что для всякого 
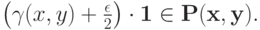
Это верно потому, что, начиная с 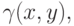 векторы
векторы  уже лежат в
уже лежат в  . Значит, по лемме 8.5,
. Значит, по лемме 8.5,
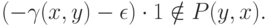
Но, с другой стороны,
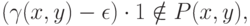
так как 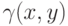 не лежит в
не лежит в  . Следовательно, наоборот:
. Следовательно, наоборот:
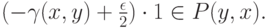
Таким образом, у нас получилось, что для любого 
 но при этом
но при этом
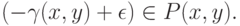
Второй этап: поделим  пополам и рассмотрим векторы
пополам и рассмотрим векторы

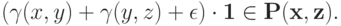
Только что мы доказали, что
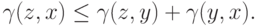
Обратное неравенство легко доказать, если поменять в этом неравенстве буквы  и
и 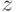 местами:
местами:
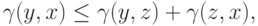
а затем заменить  на
на  :
:
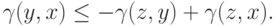
Итого мы получили два противоположных неравенства, то есть доказали искомое равенство  .
.
Теперь мы можем сдвинуть множества  . Введем новые множества
. Введем новые множества
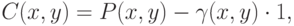
для того чтобы  . Иначе говоря,
. Иначе говоря,
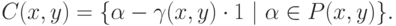
Также обозначим через  внутренность
внутренность  ; формально говоря:
; формально говоря:
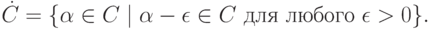
Лемма 8.7. Внутренности всех  совпадают:
совпадают:
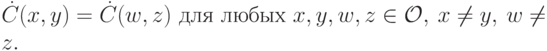
Доказательство. По второму пункту леммы 8.6,
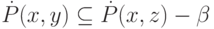
для любого  . Также это верно для
. Также это верно для 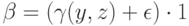 .
.
Аналогично,
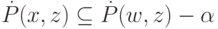
для любого  и получается, что
и получается, что
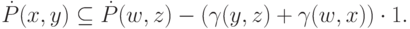
Также по второму пункту леммы 8.6,
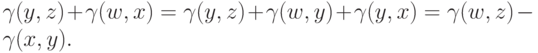
Перенося вправо  получаем, что
получаем, что
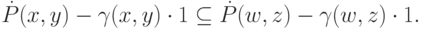
Тогда, поскольку  и
и 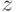 мы выбирали произвольно, получается, что все
мы выбирали произвольно, получается, что все 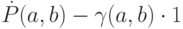 равны, то есть равны все
равны, то есть равны все  .
.
Cтоит заметить, что для неразличающихся  утверждение леммы 8.7 тоже выполняется. Докажем, например, что
утверждение леммы 8.7 тоже выполняется. Докажем, например, что  . Для доказательства выберем
. Для доказательства выберем  отличный от
отличный от  и
и  и используем лемму 8.7 для пар равенств из следующей цепочки
и используем лемму 8.7 для пар равенств из следующей цепочки

Оставляем читателю доказательство остальных случаев частичного равенства  между собой.
между собой.
Доказав, что всевозможные 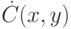 равны, обозначим их все через
равны, обозначим их все через  . Теперь, в полном соответствии с общей идеей доказательства, можно доказать, что
. Теперь, в полном соответствии с общей идеей доказательства, можно доказать, что  выпукло.
выпукло.
Лемма 8.8.  выпукло.
выпукло.
Доказательство. Пусть  . Для начала покажем, что
. Для начала покажем, что 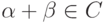 . Зафиксируем разные
. Зафиксируем разные  . Тогда
. Тогда
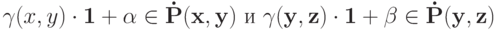
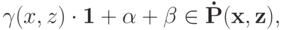
и, следовательно,  .
.
Вторая часть выпуклости – покажем, что если  то и
то и  . Предположим противное: пусть
. Предположим противное: пусть  но
но 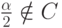 . Тогда
. Тогда
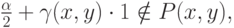
а значит,
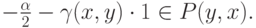
Следовательно, 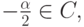 и
и  . Противоречие.
. Противоречие.
Таким образом, для всех  то есть
то есть  выпукло.
выпукло.
Теперь, наконец-то, можно завершать доказательство теоремы. Во-первых, 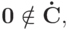 так как нулевой вектор должен быть на границе: мы уже видели, что если
так как нулевой вектор должен быть на границе: мы уже видели, что если  то
то  .
.
Вспомним теорему о подпирающей гиперплоскости: если есть выпуклое множество и есть точка, которая не лежит в его внутренности, то через нее можно провести такую гиперплоскость, что замыкание всего множества будет лежать по одну сторону от этой гиперплоскости. Значит, в нашей ситуации существует вектор  для которого
для которого  для любого
для любого 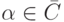 (в замыкании). Этот вектор
(в замыкании). Этот вектор  и будет теми константами
и будет теми константами  которые нам нужно найти для того, чтобы построить аффинный максимизатор.
которые нам нужно найти для того, чтобы построить аффинный максимизатор.
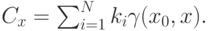
Докажем теперь все необходимые неравенства, то есть
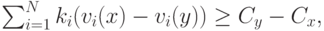
где  . Если
. Если 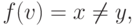 то
то  . Обозначим
. Обозначим
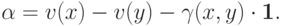
Тогда, по определению констант  и
и 
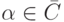 . Значит,
. Значит,  .
.
Так как  то
то
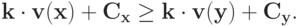
Это и есть утверждение теоремы, так как мы его доказали для произвольного  . Доказательство теоремы 8.1 тем самым завершено.
. Доказательство теоремы 8.1 тем самым завершено.

 . Cложим их:
. Cложим их: и
и