Теорема об эквивалентности доходности
Правдивость и эквивалентность доходности
Рассмотрим прямой механизм  . Напомним, что в нем у участников просто спрашивают их скрытую стоимость:
. Напомним, что в нем у участников просто спрашивают их скрытую стоимость:  , и механизм можно рассматривать как два правила:
, и механизм можно рассматривать как два правила:
-
правило распределения (allocation rule)
 определяет вероятность того, что агент
определяет вероятность того, что агент  получит объект ;
получит объект ; -
правило выплаты (payment rule)
 определяет ожидаемую выплату агента
определяет ожидаемую выплату агента  .
.
Тогда исходы механизма определяются как множество пар значений этих функций для всевозможных векторов ставок:
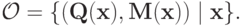
Введем два важных обозначения. Обозначим через 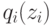 ожидаемую доходность агента
ожидаемую доходность агента  , когда он говорит
, когда он говорит 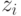 , а остальные говорят правду:
, а остальные говорят правду:

А через  — его ожидаемую выплату в этой ситуации:
— его ожидаемую выплату в этой ситуации:
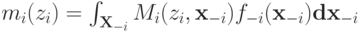
(в этих формулах, а также в дальнейшем, 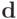 означает многомерный дифференциал, например
означает многомерный дифференциал, например  ). Тогда ожидаемый доход агента
). Тогда ожидаемый доход агента  , если он говорит
, если он говорит 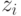 , получается как
, получается как
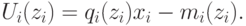
Теперь можно определить правдивость механизма в этих обозначениях.
Лемма 4.1. Прямой механизм  является правдивым тогда и только тогда, когда
является правдивым тогда и только тогда, когда
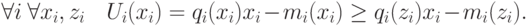
 называется равновесной функцией дохода.
называется равновесной функцией дохода.
Доказательство. Собственно, неравенство, которое приведено в формулировке леммы, и исчерпывает доказательство: для правдивости относительно агента  нужно, чтобы его ожидаемый доход при правдивой ставке был не ниже, чем при любой другой ставке; это должно происходить в ожидании по типам всех остальных агентов.
нужно, чтобы его ожидаемый доход при правдивой ставке был не ниже, чем при любой другой ставке; это должно происходить в ожидании по типам всех остальных агентов.
Ничего содержательно нового в этой вариации определения нет: по-прежнему механизм правдив, если выгодно говорить правду. Новизна — в удачно подобранных определениях, которые нам позволят доказать несколько важных свойств.
Теорема 4.2. (свойства правдивых механизмов). Каждый правдивый механизм  с равновесными функциями дохода
с равновесными функциями дохода 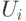 обладает следующими свойствами:
обладает следующими свойствами:
- Для каждого

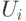 является выпуклой функцией.
является выпуклой функцией. - Для каждого
 функция
функция  является неубывающей.
является неубывающей. - Функция ожидаемого дохода агента с точностью до константы зависит только от правила распределения
 , но не от правила выплаты
, но не от правила выплаты  .
.
Более того, второе из этих свойств на самом деле равносильно правдивости.
- Если для некоторого механизма
 функции
функции  являются неубывающими, то
являются неубывающими, то  правдив.
правдив.
Доказательство.
- Выпуклость
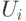 .
. 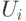 выпукла, потому что она является максимумом аффинных функций:
выпукла, потому что она является максимумом аффинных функций: .
. - Неубывание
 . Перепишем формулу для
. Перепишем формулу для  :
: .
.Значит,
 .
.Всякая выпуклая функция абсолютно непрерывна и, следовательно, дифференцируема почти всюду в своей области определения. Значит,
 почти всюду. И опять же, раз
почти всюду. И опять же, раз 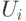 выпуклая, то, значит, ее вторая производная неотрицательна, а это означает, что ее первая производная
выпуклая, то, значит, ее вторая производная неотрицательна, а это означает, что ее первая производная  не убывает. Иначе говоря, если больше предложите, вероятность получить вещь не уменьшится.
не убывает. Иначе говоря, если больше предложите, вероятность получить вещь не уменьшится. - Независимость от правила выплаты. Абсолютно непрерывная функция представляет собой интеграл от своей производной:
 .
.Вот мы и получили, что форма ожидаемого дохода агента зависит только от правила распределения, но не от правила выплаты. Правило же выплаты определяет только
 (это называется эквивалентностью наград, payoff equivalence).
(это называется эквивалентностью наград, payoff equivalence). - Неубывание
 влечет правдивость механизма. Правдивость механизма по определению означает
влечет правдивость механизма. Правдивость механизма по определению означает .
.Но мы знаем, что
 .
.Значит,
 .
.Но если
 не убывает, это неравенство верно. Получилось, что из неубывания
не убывает, это неравенство верно. Получилось, что из неубывания  следует правдивость механизма.
следует правдивость механизма.
Обобщив все вышесказанное и вспомнив, что

можно сформулировать еще одну, более общую формулировку теоремы эквивалентности доходности.
Теорема 4.3. (теорема эквивалентности доходности). Если прямой механизм  правдив, то для всех
правдив, то для всех  и
и  ожидаемая выплата равна
ожидаемая выплата равна
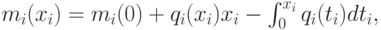
и это означает, что ожидаемая выплата агента с точностью до константы зависит только от правила распределения.
Это обобщает наш предыдущий результат (теорема 4.1) — теперь агенты могут быть несимметричными, и правила распределения тоже могут различаться. Предыдущая теорема получается как частный случай: если агенты симметричны, есть неубывающая равновесная стратегия и объект распределяется покупателю с наивысшей ставкой, то правила распределения у всех таких аукционов совпадают и зависят только от распределения  .
.
Когда теорема не помогает
Теорема об эквивалентности доходности — мощный инструмент, и теоретически она подтверждает, что доход продавца и ожидаемая прибыль участников от формы аукциона не особенно зависят. Разве что аукционер решит собрать со всех по лишнему доллару — тогда у всех доходность уменьшится на доллар, но смысл аукциона не изменится.
Однако практика не всегда подтверждает теорию; на практике есть некоторые вещи, в основном психологические, которые иногда приводят к тому, что агенты действуют не оптимально (точнее, не так, как планировалось, что для них будет оптимально).
В 2004 году компания Google решила весьма оригинально выйти на рынок. Их IPO прошло в виде большого голландского аукциона: потенциальные инвесторы выставляли заявки на цены, по которым они готовы купить акции Google, а конечная цена устанавливалась как наивысшая из всех, по которым на все акции еще нашелся бы покупатель. Google таким образом надеялся максимизировать доход от IPO.
Все прошло очень хорошо, но все же не настолько хорошо, насколько ожидалось изначально. Экономисты предполагали, что акции Google будут проданы по ценам между $108 и $135. Однако на самом деле по итогам аукциона они колебались между $85 и $95. Как можно объяснить эту "неудачу" (в кавычках, потому что на самом деле Google и так вышел на рынок очень уверенно, и его акции долгое время были одним из лучших вложений на рынке ценных бумаг)? Мог ли Google, выбрав другую модель IPO (другую модель аукциона или продажу по фиксированной цене), увеличить свои доходы от первого дня торгов?
Во-первых, могли сыграть роль психологические факторы. Специалисты отмечают, что голландский аукцион не понравился многим потенциальным инвесторам, в том числе по сугубо психологическим причинам: старый, редко ныне используемый формат, вряд ли что-то хорошее из него выйдет...
А во-вторых, и в-главных, теорема об эквивалентности доходности верна только для нейтральных к риску агентов. Для осторожных агентов она неверна, и разные модели аукционов приводят к разным доходностям для продавца. А инвесторам, особенно после неоднократного краха доткомов и при общей нестабильности рынка высоких технологий, свойственна осторожность. Поэтому, возможно, Google мог бы оптимизировать свой доход, используя другой формат IPO.
