Введение в дизайн механизмов
Несколько забавных примеров
В этом параграфе мы приведем несколько интересных примеров, позволяющих более детально рассмотреть сложности, с которыми нам предстоит столкнуться, а также еще немного мотивировать изучение дизайна механизмов.
1. Дилемма заключенного. Мы начнем с так называемой дилеммы заключенного (prisoner's dilemma) — с классического примера из теории игр. Двое заключенных сидят в тюрьме. Им предлагают признаться в преступлении, заложив тем самым своего сообщника. Реальных доказательств главного пункта обвинения у прокуратуры нет, следователи могут рассчитывать только на помощь самих заключенных. Поэтому каждому из них предлагают сделку:
- если оба заключенных промолчат, то оба отсидят по полгода за другие грешки;
- если оба признаются, то обоим за такое примерное поведение дадут по два года;
- но если один признается, а другой нет, то признавшегося за сотрудничество вообще отпустят, а упорствующему впаяют по полной, лет десять.
Держать связь заключенные не могут. Как же поступить каждому из них?
Вот какая получается матрица возможных стратегий этой игры:
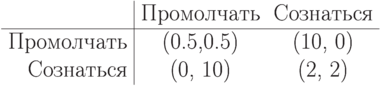
Посмотрите, как интересно получается: вне зависимости от выбора первого заключенного второму в любом случае выгоднее признаться! Получается, что для каждого из них "Сознаться" — доминантная стратегия, и в результате... они будут сидеть по 2 года, а не по 0.5. Равновесие получается в доминантных стратегиях, но для каждого из игроков оно неоптимально! И все это получилось благодаря разумным действиям следователя, который смог разработать правильный дизайн "игры" с заключенными.
Может показаться, что это абстрактный пример, не имеющий ничего общего с реальностью. Однако легко привести вполне жизненный пример, в котором возникает именно дилемма заключенного. Рассмотрим рынок, на котором две фирмы выпускают совершенно аналогичные продукты, и других производителей на рынке этого продукта нет. Как будут распределяться доходы компаний по отношению к их возможным рекламным кампаниям?
Если рекламы не будет вообще, у них будет одно распределение рынка, определенное производственными мощностями и другими факторами (сетью реализации, например). Предположим, что они обе будут получать прибыль по  . Если они обе будут активно рекламироваться, то реклама "взаимно сократится", потребитель будет хорошо осведомлен об обоих продуктах, и относительное потребление их продуктов не изменится. Но деньги на рекламу будут потрачены (обозначим их через
. Если они обе будут активно рекламироваться, то реклама "взаимно сократится", потребитель будет хорошо осведомлен об обоих продуктах, и относительное потребление их продуктов не изменится. Но деньги на рекламу будут потрачены (обозначим их через  , от "advertising")! Таким образом, ситуация, когда обе фирмы рекламируются, хуже для них обеих. Но если одна фирма не будет рекламироваться, а вторая будет, то та, что будет, получит куда большую прибыль от резко увеличившейся доли рынка (для простоты предположим, что доля рынка вырастет до 100%).
, от "advertising")! Таким образом, ситуация, когда обе фирмы рекламируются, хуже для них обеих. Но если одна фирма не будет рекламироваться, а вторая будет, то та, что будет, получит куда большую прибыль от резко увеличившейся доли рынка (для простоты предположим, что доля рынка вырастет до 100%).
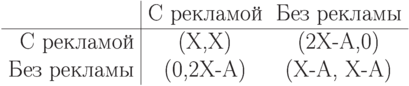
Вот вам и классическая дилемма заключенного. Кстати, гонка вооружений во время холодной войны тоже неплохо укладывается в эту схему.
2. Трагедия общин. Второй пример — так называемая трагедия общин. Этот пример имеет внушительную историю: он известен еще из Фукидида и Аристотеля. Трагедия общин возникает, когда у нескольких игроков на рынке есть некий общий ресурс. Выгоды от его использования индивидуальны, а затраты на использование общие, поэтому все пытаются максимизировать свое собственное использование ресурса, и ресурс истощается для всех.
Классическая постановка выглядит так: на принадлежащем городу пастбище пасут овец несколько местных овцеводов. Пастбище общее и бесплатное, а каждая дополнительная овца приносит овцеводу прибыль. Поэтому все начинают разводить все больше и больше овец, и пастбище окончательно вытаптывается. Однако при этом каждый овцевод полностью рационален, потому что лично для него дополнительная овца значит гораздо больше, чем дополнительный ущерб пастбищу от одной овцы.
Такие примеры возникают все время там, где есть общие ресурсы, которые трудно разделить: при загрязнении окружающей среды, использовании воды и воздуха, вырубке лесов, охоте, рыболовстве и в других аналогичных ситуациях. Решения в хорошем смысле этого слова — чтобы все сами по себе стали разумно использовать общий ресурс — у этой задачи нет (потому и трагедия, наверное). Решение может заключаться только в том, чтобы построить (при помощи государства) некий общественный механизм, например механизм налогообложения или квотирования, при котором общий ресурс не истощится. Вопрос, как сделать это наиболее эффективно, — предмет теории механизмов.
3. Парадокс аукциона за доллар. Это пример того, к чему может привести дизайн хитрых механизмов.
Рассмотрим такой аукцион: лот — один доллар, участники могут последовательно поднимать цену (как в самом обычном аукционе), давший максимальную цену платит ее и получает доллар. Но при этом — вот где дьявол в деталях — максимальные объявленные цены должны будут уплатить все участники аукциона, а не только победитель.
Участники, разумеется, действуют рационально. Пусть минимальная разность между соседними ставками — один цент. Первый участник, желая заработать 99 центов, объявляет цену в один цент. Второй перебивает ее двумя центами, третий — тремя... Тут первый решает, что заработать 96 центов куда лучше, чем потерять один, и объявляет цену в 4 цента. И так далее.
Рано или поздно цена достигнет 98 центов (пусть такую цену в очередном раунде дал первый участник). Второй участник, желая заработать один цент, дает цену в 99 центов. Но для первого даже остаться в нуле гораздо лучше, чем потерять те 98, которые он уже объявлял! И он ставит 100 центов за доллар. А второй... ставит 101!
Адекватного решения у этого парадокса нет. Собственно, и "парадокса" нет — у игры нет равновесия, и игроки могут в конце концов отдать хитрому аукционеру все свои деньги. С другой стороны, конечно, "рациональность" игроков в этом аукционе тоже под вопросом: когда игрок решает, что выгоднее — потерять 98 центов или получить доллар за 100 центов, вторая альтернатива не равна нулю, а должна принимать во внимание вероятность того, что его оппонент не остановится и сделает новую ставку. Ожидание выигрыша составляет бесконечный расходящийся ряд потерь. С третьей же стороны, если все будут так "рационально" рассуждать, то никто не начнет торг, и не такой умный первый игрок, объявивший цену в один цент, спокойно получит свои 99 центов прибыли. Игры без равновесия — непростое дело...
4. Winner's curse. Возьмем следующую простую ситуацию (в следующих лекциях мы рассмотрим ее гораздо подробнее): есть аукцион, на торги выставлен товар, у каждого участника свое мнение о ценности товара. Участники делают ставки, исходя из своих понятий о ценности. Выигрывает тот, кто сделал самую большую ставку.
Предположим, что истинную стоимость объекта участники доподлинно не знают, у них есть некоторая общая информация, а дальше происходят отклонения и в большую, и в меньшую сторону. Иначе говоря, предположим, что мнения участников распределены приблизительно нормально вокруг истинной стоимости продаваемого товара. Такая ситуация часто возникает, например, в аукционах на нефтеносные участки: информация о количестве нефти общедоступна, но неточна. Отклонения от настоящей цены в зависимости от оптимизма или пессимизма участников и их частной информации будут и в большую, и в меньшую сторону.
Но ведь в результате аукциона победит участник с максимальным отклонением в плюс! Он наверняка объявлял стоимость выше истинной! Иначе говоря, если вы победили на этом аукционе, сам факт вашей победы означает, что вы были чересчур оптимистичны (и, как следствие, переплатили). В этом и заключается парадокс winner's curse.
4. Парадокс Браесса. Это пример так называемой "цены анархии", который подтверждает, что зачастую свободный рынок приходит отнюдь не к оптимальному решению.
Рассмотрим две точки, "Старт" и "Финиш", между которыми есть два пути, проходящие через точки  и
и  . Если машина едет по незаполненной трассе, она едет со скоростью 100 км/ч. Если трасса заполнилась, то скорость передвижения падает до
. Если машина едет по незаполненной трассе, она едет со скоростью 100 км/ч. Если трасса заполнилась, то скорость передвижения падает до

Все водители все знают, включая текущее распределение автомобилей на других дорогах, и выбирают оптимальный для себя маршрут.
Понятно, что в этой симметричной ситуации водители будут выбирать менее загруженную трассу (когда они заполнятся). Пусть проехать должны 2500 машин. Тогда 1250 из них поедут по одной дороге, а другие 1250 — по другой. При этом путь каждого водителя занимает

(в числителе первого слагаемого — единица, а не 1250/2000, потому что быстрее 100 км/ч ехать все равно не получится, даже если трасса заполнена лишь наполовину).
Но вдруг государство решило, что надо бы людям помочь быстрее добираться от старта до финиша (или, возможно, муниципалитету просто вдруг выделили кучу бюджетных денег на дорожные работы), и была построена новая короткая дорога между  и
и  . Эта дорога имеет длину всего 60 км супротив 100 км старых дорог. Важно: старые дороги никто не закрывает, у водителей просто появляется новый выбор.
. Эта дорога имеет длину всего 60 км супротив 100 км старых дорог. Важно: старые дороги никто не закрывает, у водителей просто появляется новый выбор.
Рассмотрим старое равновесие (1250 на 1250). При появлении новой дороги по ней ехать будет выгоднее, и водители будут выбирать новую дорогу до тех пор, пока все три возможных пути не сравняются по времени. Новое равновесие (когда все пути одинаковы) достигается (проверьте это!), когда из 2500 машин 1500 едут по новой дороге, а по старым — по 500. Но давайте подсчитаем время в пути:
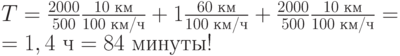
Оказывается, что, просто расширив спектр возможностей водителей, мы перевели систему из более эффективного равновесия в менее эффективное. При этом каждый водитель по отдельности действовал рационально: выбирал, где быстрее.
Замечание. Может показаться, что путей не три, а четыре: вдруг появившийся после постройки новой дороги четвертый путь
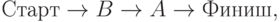
несмотря на большую длину, все-таки будет в каких-то случаях достаточно эффективным, чтобы его избрать? Но при нашей постановке задачи он все-таки будет всегда строго хуже пути 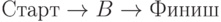 : даже если все 2500 машин едут по десятикилометровому участку
: даже если все 2500 машин едут по десятикилометровому участку 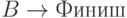 , там все равно можно добраться быстрее, чем в объезд по пустым дорогам.
, там все равно можно добраться быстрее, чем в объезд по пустым дорогам.
Важно заметить, что в некоторых формулировках парадокса Браесса новая дорога могла бы быть и на пользу. Для этого нужно было бы, грубо говоря, в пунктах "Старт" и  посадить двух регулировщиков, которые будут распределять потоки как надо.
посадить двух регулировщиков, которые будут распределять потоки как надо.
Давайте подсчитаем оптимальное время проезда в этой системе с 2500 машинами, если регулировщики работают оптимальным образом. Предположим, что регулировщик в точке "Старт" отправляет  машин к
машин к  и
и 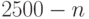 сразу к
сразу к  , а регулировщик в точке
, а регулировщик в точке  отправляет
отправляет  машин к точке "Финиш" и
машин к точке "Финиш" и  машин к
машин к  по новой дороге.
по новой дороге.
Тогда время в пути будет равно
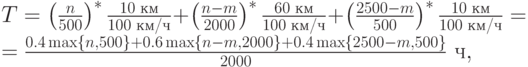
где звездочкой мы обозначили тот факт, что если числитель меньше знаменателя, то дробь равна единице. Если оптимизировать это по  и
и  ,
,
Этот эффект называется "ценой анархии" (price of anarchy): иногда регулируемый рынок действительно функционирует эффективнее, чем управляемый лишь невидимой рукой; наоборот, конечно, не бывает, потому что отсутствие вмешательства — частный случай вмешательства. Дизайн механизмов — один из способов (зачастую единственный) ввести на рынок "видимую руку" того, кто этот дизайн осуществляет.