Теория игр
Доминантные и доминируемые стратегии
Что же делать участвующим в игре агентам? Как им определить, какая стратегия лучше других?
Давайте для начала поставим перед собой более скромную цель: определить, какие стратегии точно не подойдут.
Определение 1.2. Стратегия  агента
агента 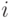 называется доминируемой, если существует такая стратегия
называется доминируемой, если существует такая стратегия  , что
, что
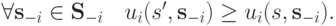
В таком случае говорят, что 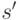 доминирует над
доминирует над  .
.
Иначе говоря, стратегия  доминируема, если существует другая стратегия, которая не хуже
доминируема, если существует другая стратегия, которая не хуже 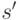 в каждой точке, при любых возможных комбинациях стратегий других агентов. Значит, нет вообще никакой причины предпочитать
в каждой точке, при любых возможных комбинациях стратегий других агентов. Значит, нет вообще никакой причины предпочитать  , и ее можно просто отбросить при анализе.
, и ее можно просто отбросить при анализе.
Пример 1.4. Вспомним пример 1.2, в котором полковник Блотто собирался расставить войска на поле. Если проанализировать матрицу из примера 1.2, станет очевидным, что стратегии  ,
,  и
и  доминируются другими: например, стратегия
доминируются другими: например, стратегия  окажется лучше любой из них. Разумеется, то же самое верно и для противника Блотто. Таким образом, матрица существенно сократится.
окажется лучше любой из них. Разумеется, то же самое верно и для противника Блотто. Таким образом, матрица существенно сократится.

Конец примера 1.4.
Пример 1.5. В примере 1.3, в котором мы обсуждали конкуренцию по Курно, было очень много доминируемых стратегий. Таковыми были все стратегии  : они гарантированно приносили неположительную прибыль, в то время как нулевая стратегия (
: они гарантированно приносили неположительную прибыль, в то время как нулевая стратегия (  , ничего не производить) гарантирует нулевую прибыль. Поэтому сразу можно было ограничиться анализом квадрата
, ничего не производить) гарантирует нулевую прибыль. Поэтому сразу можно было ограничиться анализом квадрата ![[0,2]\times [0,2]](/sites/default/files/tex_cache/a497fd8e2e402053982143694f1f7afb.png) в качестве множества стратегий.
в качестве множества стратегий.
Конец примера 1.5.
Правда, стоит заметить, что легко построить пример, в котором любая стратегия доминируема. Это будет значить, что некоторые стратегии эквивалентны, то есть доминируют друг над другом. В таких случаях хотя бы одну из них стоит оставить, а то совсем не из чего будет выбирать.
Продолжаем разговор. После доминируемых стратегий логично будет ввести доминантные стратегии.
Определение 1.3. Стратегия  агента
агента 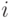 называется доминантной, если всякая другая стратегия
называется доминантной, если всякая другая стратегия  ею доминируется, то есть
ею доминируется, то есть
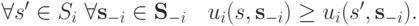
Доминантная стратегия для агента — настоящее счастье. Ему вообще думать не надо: достаточно выбрать доминантную стратегию, все равно никакая другая ни при каком исходе ничего лучшего не даст.
Более того, если у всех агентов есть доминантные стратегии, то анализ такой игры закончится, не успев начаться. Можно с уверенностью сказать, что все агенты выберут свои доминантные стратегии.
Определение 1.4. Равновесие в доминантных стратегиях для стратегической игры  — это такой профиль стратегий
— это такой профиль стратегий 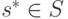 , что для всякого агента
, что для всякого агента  стратегия
стратегия  является доминантной.
является доминантной.
Такое равновесие является самым устойчивым из всех. В следующей лекции мы приведем пример из теории экономических механизмов, в котором возникает такое равновесие — так называемый аукцион Викри (см. теорему 2.1.
Но, к сожалению, счастье достижимо далеко не всегда. Ни в примере 1.1, ни в примере 1.2, ни в примере 1.3 никакого равновесия в доминантных стратегиях не получалось. Для каждой стратегии 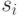 игрока
игрока 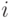 там существовал профиль стратегий других игроков
там существовал профиль стратегий других игроков  , в котором игроку
, в котором игроку 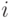 было бы выгодно сменить
было бы выгодно сменить 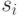 на ту или иную
на ту или иную  .
.
Равновесие Нэша
В предыдущем параграфе мы обсудили, что если у агента есть доминантная стратегия, то ему вообще размышлять и беспокоиться не о чем: он может просто выбирать эту стратегию. Но что же делать участвующим в игре агентам, когда таких стратегий нет и не предвидится?
Тогда приходится учитывать не только свои собственные стратегии, но и стратегии других агентов. Учет этот приведет к понятию равновесия, сформулированному в 1950 году Джоном Нэшем [60].
Определение 1.5. Равновесие Нэша в чистых стратегиях для стратегической игры  — это такой профиль стратегий
— это такой профиль стратегий  , что для всякого агента
, что для всякого агента  выполняется следующее условие:
выполняется следующее условие:
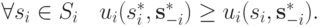
Иначе говоря, как и прежде, агенту невыгодно отклоняться от избранной стратегии  . Но теперь ему это невыгодно делать не абстрактно, при любом выборе стратегий у других агентов, а только в конкретном профиле стратегий
. Но теперь ему это невыгодно делать не абстрактно, при любом выборе стратегий у других агентов, а только в конкретном профиле стратегий  .
.
Пример 1.6. Продолжаем рассматривать беднягу Блотто. Матрица игры полковника без доминируемых стратегий была приведена в примере 1.4. Из матрицы легко видеть, что если один игрок выбирает стратегию  , то от выбора другого уже ничего не зависит, то есть можно сказать, что другому тоже нет резона отклоняться от стратегии
, то от выбора другого уже ничего не зависит, то есть можно сказать, что другому тоже нет резона отклоняться от стратегии  . Все это значит, что для данной игры профиль стратегий
. Все это значит, что для данной игры профиль стратегий  находится в равновесии Нэша.
находится в равновесии Нэша.
Конец примера 1.6.
Приведем и непрерывный пример — поверьте, нас еще ждут подобные рассуждения, и пора привыкать к чуть более серьезному анализу.
Пример 1.7. Вернемся к анализу конкуренции по Курно из примера 1.3. На этот раз мы не будем ничего упрощать: пусть цена задается неизвестной функцией  , а себестоимость производства для каждой фирмы — неизвестной функцией
, а себестоимость производства для каждой фирмы — неизвестной функцией  . Чтобы найти равновесие Нэша, найдем функцию лучшего ответа. Прибыль компании определяется как
. Чтобы найти равновесие Нэша, найдем функцию лучшего ответа. Прибыль компании определяется как

Чтобы определить максимум функции  для фиксированного
для фиксированного 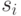 , нужно просто найти производную
, нужно просто найти производную
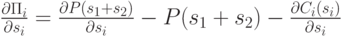
и приравнять ее к нулю. Соответственно, равновесие Нэша достигается там, где обе фирмы выдают оптимальный ответ на стратегию противника, то есть на решениях следующей системы дифференциальных уравнений:
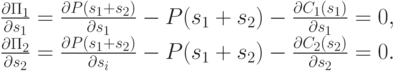
Оставим читателю удовольствие проверить, что в рассмотренном в примере 1.3 частном случае равновесием Нэша действительно будет точка пересечения прямых на рис. 1.1.
Конец примера 1.7.
В определении 1.5 упоминался странный термин "чистые стратегии": а какими еще они бывают? Оказывается, что стратегии бывают не только чистыми, но и смешанными. Смешанные стратегии — логичное расширение понятия стратегии: давайте разрешим игроку не только выбирать одну из  , но и делать из них более или менее случайный выбор.
, но и делать из них более или менее случайный выбор.
Определение 1.6. Смешанная стратегия для игрока 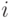 в стратегической игре
в стратегической игре  — это распределение вероятностей
— это распределение вероятностей  , где
, где 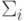 — множество всех распределений вероятностей над
— множество всех распределений вероятностей над 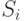 .
.
Смешанную стратегию также можно рассматривать как задание весов для каждой стратегии так, чтобы сумма (в непрерывном случае — интеграл) всех весов была равна 1.
Бывают игры, где нет равновесий Нэша для чистых стратегий. Но оно всегда (в конечном случае) есть в смешанных стратегиях.
Пример 1.8. Вспомним игру "камень-ножницы-бумага", матрицу которой мы уже выписывали в примере 1.1.

Очевидно, что никакого равновесия Нэша в чистых стратегиях здесь нет: для любой стратегии найдется кому ее опровергнуть. Но равновесие Нэша в смешанных стратегиях здесь имеется. Предположим, что второй игрок выбирает камень, ножницы или бумагу с вероятностью  , а первый выбирает их с вероятностями
, а первый выбирает их с вероятностями 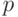 ,
, 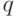 и
и  . Тогда первый игрок выигрывает с вероятностью
. Тогда первый игрок выигрывает с вероятностью
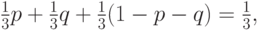
а также проигрывает и делает ничью с той же вероятностью. Иначе говоря, если противник выбирает стратегию равновероятно, для игрока все стратегии эквивалентны. Поскольку игра симметрична, получается, что профиль смешанных стратегий
![\left[\left(\frac{1}{3},\frac{1}{3},\frac{1}{3}\right),\left(\frac{1}{3},\frac{1}{3},\frac{1}{3}\right)\right]](/sites/default/files/tex_cache/fcafc3b3e52134e48a2f4a4512d69aba.png)
находится в равновесии.
Конец примера 1.8.
Доказательство того, что равновесие в смешанных стратегиях всегда существует, следует из теоремы Какутани о неподвижной точке [12,31].
Теорема 1.1 (Какутани) Пусть  — непустое выпуклое компактное подмножество евклидова пространства
— непустое выпуклое компактное подмножество евклидова пространства  , а
, а  — многозначная функция на
— многозначная функция на  с замкнутым графиком, такая, что множество
с замкнутым графиком, такая, что множество  непусто, замкнуто и выпукло для всех
непусто, замкнуто и выпукло для всех  . Тогда у
. Тогда у  есть неподвижная точка:
есть неподвижная точка:  .
.
Замечание. Чтобы понять условие теоремы, обычно лучше всего привести пример, в котором без одного из условий теорема оказывается неверной. Вот и здесь: давайте рассмотрим многозначную функцию на единичном отрезке ![f:[0,1]\to 2^{[0,1]}](/sites/default/files/tex_cache/12abe8c85300c75f1e3da32bf5609282.png) , заданную как
, заданную как
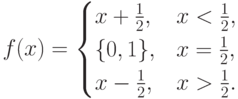
Получилась функция с замкнутым графиком (график ее изображен на рис. рис. 1.2), но прямую  он не пересекает, а все потому, что в точке
он не пересекает, а все потому, что в точке  график не является выпуклым (если замкнуть его по выпуклости в этой точке, то она и будет неподвижной для
график не является выпуклым (если замкнуть его по выпуклости в этой точке, то она и будет неподвижной для  ). Ну а для любой функции, удовлетворяющей всем условиям теоремы, все в порядке: вот, например, на рис. рис. 1.3 функция
). Ну а для любой функции, удовлетворяющей всем условиям теоремы, все в порядке: вот, например, на рис. рис. 1.3 функция ![f(x)=\left[\frac12-\frac12x,1-x\right]](/sites/default/files/tex_cache/5b779ce8ea9494363f608c682c4f6f98.png) , заданная на все том же отрезке
, заданная на все том же отрезке ![S=[0,1]](/sites/default/files/tex_cache/955cbecda23de7c1d1294af5e571e1a5.png) . Как видно, она пересекает прямую
. Как видно, она пересекает прямую  (причем далеко не в одной точке);
(причем далеко не в одной точке);  -координаты всего этого пересечения представляют собой неподвижные точки функции
-координаты всего этого пересечения представляют собой неподвижные точки функции  .
.
Следствие 1.1.1. В любой конечной игре существует равновесие Нэша в смешанных стратегиях.
Каждая смешанная стратегия есть распределение вероятностей на множестве возможных действий агента, а значит, сумма этих вероятностей равна единице. Но в  -мерном евклидовом пространстве симплекс
-мерном евклидовом пространстве симплекс
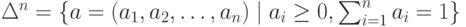
является выпуклым компактным множеством. Выигрыш игрока в игре со смешанными стратегиями есть математическое ожидание вида
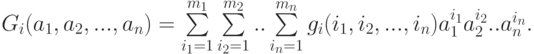
Эта функция является линейной и непрерывной по  при фиксированных остальных аргументах. Следовательно, по теореме Какутани, у этой функции будет неподвижная точка. Это и означает существование равновесия по Нэшу в играх со смешанными стратегиями.
при фиксированных остальных аргументах. Следовательно, по теореме Какутани, у этой функции будет неподвижная точка. Это и означает существование равновесия по Нэшу в играх со смешанными стратегиями.
Говорят, в 1949 году Нэш рассказал фон Нейману о своей новой идее насчет равновесия для смешанных стратегий. Фон Нейман в своем стиле ответил: "Это, знаете ли, тривиально; это же всего лишь теорема о неподвижной точке". Позже Нэшу за это "тривиальное наблюдение" дали Нобелевскую премию (хотя, конечно, не только за него).


