|
Неоднократно находил ошибки в тестах, особенно в экзаменационных вопросах, когда правильно данный ответ на вопрос определялся в итоге как не правильно отвеченный... Из-за этого сильно страдает конечный бал! Да еще в заблуждение студентов вводит! Они-то думают, что это они виноваты!!! Но они тут не причем! Я много раз проверял ответы на некоторые такие "ошибочные" вопросы по нескольким источникам - результат везде одинаковый! Но ИНТУИТ выдавал ошибку... Как это понимать? Из-за подобных недоразумений приходиться часами перерешивать экзамен на отличную оценку...!!! Исправьте, пожалуйста, такие "ошибки"... |
Дополнительные встраиваемые элементы контроля в механизмах параллельной структуры
Дополнительные встраиваемые элементы контроля.
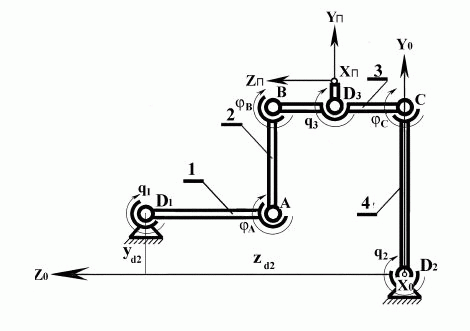
В лекциях 13 и 14 излагается возможность расширения функциональных характеристик и интеллектуальных свойств системы <<низшего>> уровня путем установки дополнительных датчиков и приводов. Дополнительные встраиваемые элементы контроля в механизмах параллельной структуры существенно упрощают вычисление положения выходного звена, а также дают возможность повысить точность определения его положения. Рассмотрим данную задачу на примере механизма, представляющего манипулятор перемещения изделия специального робота-станка для обработки пера лопаток (рис. 10.4). Представим данный рисунок с некоторым уточнением (рис. 13.1) и рассмотрим управление только плоским пятизвенником. Манипулятор имеет три управляемых двигателя D1, D2, D3 для перемещения выходного звена по трем координатам: двум линейным и одному углу поворота выходного звена в плоскости Y00Z0. Кроме датчиков контроля углов поворота двигателей q1,q2 и q3
, в механизме установлены датчики измерения углов взаимного положения звеньев, расположенные в сочленениях 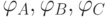 .
.
Для определения положения выходного звена (XYZ)П относительно базовой системы координат (XYZ)0 достаточно знать длины звеньев L1 L4, yd2, zd2 и три угла поворота. При наличии шести датчиков контроля углового положения звеньев q1,q2,q3 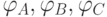 требуется найти такое сочетание трех из шести: C63 информационных датчиков углового положения, которое обеспечит минимальную погрешность определения координат выходного звена механизма относительно (XYZ)0. Следует отметить, что при рассмотрении только линейных перемещений выходного звена достаточно из пяти датчиков q1,q2,
требуется найти такое сочетание трех из шести: C63 информационных датчиков углового положения, которое обеспечит минимальную погрешность определения координат выходного звена механизма относительно (XYZ)0. Следует отметить, что при рассмотрении только линейных перемещений выходного звена достаточно из пяти датчиков q1,q2, 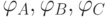 выбрать только два.
выбрать только два.
Рассмотрим решение данной задачи в общем случае. Связь между вектором, определяющим погрешности выходного звена механизма, -  (в общем случае размерности 6x1 ) и погрешностями информационных датчиков qj (размерности nx1, где n>6 ) однозначно выражается линейной зависимостью
(в общем случае размерности 6x1 ) и погрешностями информационных датчиков qj (размерности nx1, где n>6 ) однозначно выражается линейной зависимостью
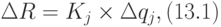
где Kj - матрица весовых множителей 6 x n. Вектор ![\Delta R=[\Delta r_{i}]^{T}](/sites/default/files/tex_cache/406760c70a909e3f80db337ae7f9ab9f.png) включает погрешность линейных координат
включает погрешность линейных координат  и
и  в точке i конечного звена механизма и погрешность угловых координат
в точке i конечного звена механизма и погрешность угловых координат  и
и  вокруг данных осей,
вокруг данных осей,
![\Delta R=[\Delta r_{i}]^{T}=[\Delta x\Delta y\Delta z\Delta \varphi \Delta \Phi \Delta \theta ]^{T}.](/sites/default/files/tex_cache/63993d1603f7281e11e8cdc531691edc.png)
Погрешности определяются в неподвижной или связанной с деталью системах координат.
Общее возможное количество датчиков, с помощью которых можно определить положение выходного звена механизма параллельной структуры, для механизма, имеющего m степеней свободы, равно n=m2. Максимальное число возможных сочетаний информационных датчиков, которое может быть взято для определения положения выходного звена, вычисляется соотношением
Cnm=(n(n-1)(n-2)...(n-m+1))/(1x2x3x...xm) .
Для шестистепенного механизма
C366=(36x35x34x33x32x31)/(1x2x3x4x5x6)=1947792.
Чаще всего требуется обеспечить высокую точность вычисления линейных координат. В этом случае число возможных вариантов определения трех линейных координат составляет C363=7140 и одной координаты C361=36.
Для механизма, представленного на рисунке 13.1, выходным звеном плоского пятизвенника D1,A,B,C,D2 является звено L3, на котором располагается привод q3. Две линейные координаты, определяющие положение центра привода q3, могут быть определены датчиками углов q1,q2 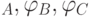 различным их сочетанием по два: C52=10. Поэтому число способов вычисления координат выходного звена в этом случае также равно 10.
различным их сочетанием по два: C52=10. Поэтому число способов вычисления координат выходного звена в этом случае также равно 10.
Вычисление и анализ элементов матрицы Kj является основной задачей при выборе информационных датчиков, определяющих координаты выходного звена механизма. Элементы данной матрицы являются весовыми множителями при погрешностях датчиков и определяют вклад погрешности каждого датчика в погрешность соответствующей координаты выходного звена механизма. Рассмотрим способ определения данных весовых множителей.