|
Неоднократно находил ошибки в тестах, особенно в экзаменационных вопросах, когда правильно данный ответ на вопрос определялся в итоге как не правильно отвеченный... Из-за этого сильно страдает конечный бал! Да еще в заблуждение студентов вводит! Они-то думают, что это они виноваты!!! Но они тут не причем! Я много раз проверял ответы на некоторые такие "ошибочные" вопросы по нескольким источникам - результат везде одинаковый! Но ИНТУИТ выдавал ошибку... Как это понимать? Из-за подобных недоразумений приходиться часами перерешивать экзамен на отличную оценку...!!! Исправьте, пожалуйста, такие "ошибки"... |
Системы контроля геометрических параметров и распознавания качества обрабатываемых поверхностей
Контроль изделий сложной формы в составе технологических систем.
В составе технологического комплекса оптическая система может быть применена для контроля геометрических размеров поверхности, определения границ контура детали. На рисунке 12.9 приведена конструкция оптической системы в составе робота—станка. Прежде всего для определения геометрических параметров анализируемой поверхности и их погрешностей введем основные координатные системы, относительно которых осуществляется преобразование оптического изображения.
Основной координатной системой, относительно которой определяются геометрические параметры поверхности и ее погрешности, является система координат детали (XYZ)д. Для пера лопаток турбинных двигателей ось Zд направлена вдоль оси лопатки, ось Xд — по "ширине" поверхности пера лопатки и ось Yд образует правую систему координат и направлена по "толщине" пера. При этом выпуклую часть поверхности пера обычно называют "спинкой", а вогнутую "корытом".
На плоскость Zд0Xд под углом к данной плоскости падает параллельный пучок света, проходящий через дифракционную решетку (рис. 12.4) в направлении стрелки B (рис. 12.9). Благодаря этому на плоскости Zд0Xд образуется сетка из параллельных линий "зебра". Данные линии параллельны между собой, а также исходя из конструктивного расположения дифракционной решетки (рис. 12.10), остаются параллельными оси 0Xд. Уравнения плоскостей параллельных пучков света, проходящих через дифракционную решетку и образующих параллельные линии ("зебру") на плоскости Zд0Xд можно представить в виде
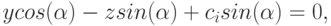 |
( 12.14) |
где ci — координата z для каждого луча, расположенного в координатной плоскости Zд0Yд.
В плоскости, параллельной Zд0Xд, на расстоянии OD (для рассматриваемой на рис. 12.9 системы это расстояние равно OD=1120 мм) располагается фотоматрица, на которую проецируется изображение "зебры".
Лучи, отраженные от поверхности, через оптическую систему с фокусным расстоянием f попадают на фотоматрицу. В этом случае принимается, что каждый луч, отраженный от поверхности, проходит через фокус (точку F ) с координатами (0,yf,zf), задаваемыми в системе координат (XYZ)д. Для обеспечения симметричности преобразований принимается, что фокус располагается в плоскости Zд0Yд.
Параллельность плоскости расположения фотоматрицы и плоскости Zд0Xд должна создаваться специальной настройкой, обеспечивающей симметричность изображения на фотоматрице точек, симметрично расположенных в плоскости Zд0Xд, относительно перпендикуляра, опущенного из точки F на плоскость Zд0Xд.
Рассмотрим сложную поверхность, располагаемую таким образом, чтобы отраженные от нее лучи полностью попадали в телекамеру. Параллельные лучи, проходящие через светлые линии дифракционной решетки, образуют плоские сечения, рассекающие поверхность и образующие линии, проецируемые на фотоматрицу (рис. 12.10).
Оптическая система позволяет определять координаты точек поверхности в системе координат (XYZ)д. Отраженные от анализируемой поверхности линии "зебры" на плоскости фотоматрицы образуют искаженные линии "зебры". В данном случае рассматриваются непрерывные координаты линий в плоскости фотоматрицы, получаемые уже после обработки границ зон светлых и темных полос и их аппроксимации в соответствии с методикой, изложенной выше. Координаты точек на фотоматрице задаются в системе координат (XYZ)д.
По координатам точек линий "зебры", определяемых в плоскости Zф0Xф, определяются координаты точек данных линий на анализируемой поверхности (рис. 12.10) в системе (XYZ)д. Рассмотрим методику определения координат для одной из точек линии поверхности, например, точки A (рис. 12.10), образованной пересечением плоскости параллельных лучей с поверхностью, по координатам данной точки (т. A* ) на фотоматрице — A*(xA*,yA*,zA*). Если данные координаты известны, то уравнение прямой, проходящей через две точки F и A* в системе координат (XYZ)д, принимает вид
Координаты точки A поверхности, соответствующие ее координатам на плоскости фотоматрицы, получаются пересечением прямой (12.15) с соответствующей плоскостью параллельных лучей (12.14). Совместное решение системы уравнений, полученной из (12.14) и (12.15),
относительно x, y и z позволяет определить координаты т. A поверхности. С учетом того, что yA*=OD и xf=0, получим
Аналогично могут быть вычислены координаты всех точек линий "зебры" на анализируемой поверхности по их координатам в плоскости расположения фотоматрицы.





