|
Неоднократно находил ошибки в тестах, особенно в экзаменационных вопросах, когда правильно данный ответ на вопрос определялся в итоге как не правильно отвеченный... Из-за этого сильно страдает конечный бал! Да еще в заблуждение студентов вводит! Они-то думают, что это они виноваты!!! Но они тут не причем! Я много раз проверял ответы на некоторые такие "ошибочные" вопросы по нескольким источникам - результат везде одинаковый! Но ИНТУИТ выдавал ошибку... Как это понимать? Из-за подобных недоразумений приходиться часами перерешивать экзамен на отличную оценку...!!! Исправьте, пожалуйста, такие "ошибки"... |
Методы поиска решений
Задачи планирования последовательности действий
Многие результаты в области ИИ достигнуты при решении " задач для робота ". Одной из таких простых в постановке и интуитивно понятных задач является задача планирования последовательности действий, или задача построения планов.
В наших рассуждениях будут использованы примеры традиционной робототехники (современная робототехника во многом основывается на реактивном управлении, а не на планировании). Пункты плана определяют атомарные действия для робота. Однако при описании плана нет необходимости опускаться до микроуровня и говорить о датчиках, шаговых двигателях и т. п. Рассмотрим ряд предикатов, необходимых для работы планировщика из мира блоков. Имеется некоторый робот, являющийся подвижной рукой, способной брать и перемещать кубики. Рука робота может выполнять следующие задания ( U, V, W, X, Y, Z - переменные).
goto(X,Y,Z) перейти в местоположение X, Y, Z
pickup(W) взять блок W и держать его
putdown(W) опустить блок W в некоторой точке
stack(U,V) поместить блок U на верхнюю грань блока V
unstack(U,V) убрать блок U с верхней грани блока V
Состояния мира описываются следующим множеством предикатов и отношений между ними.
on(X,Y) блок X находится на верхней грани блока Y
clear(X) верхняя грань блока Х пуста
gripping(X) захват робота удерживает блок Х
ontable(W) блок W находится на столе
Предметная область из мира кубиков представлена на рис. 3.8 в виде начального и целевого состояния для решения задачи планирования. Требуется построить последовательность действий робота, ведущую (при ее реализации) к достижению целевого состояния.
Состояния мира кубиков представим в виде предикатов. Начальное состояние можно описать следующим образом:
start = [handempty, ontable(b),
ontable(c), on(a,b), clear(c),
clear(a)]где: handempty означает, что рука робота Робби пуста.
Целевое состояние записывается так:
goal = [handempty, ontable(a),
ontable(b), on(c,b), clear(a),
clear(c)]Теперь запишем правила, воздействующие на состояния и приводящие к новым состояниям.
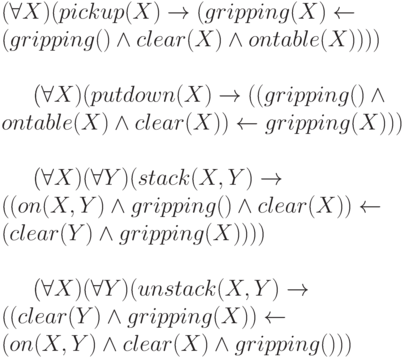
Прежде чем использовать эти правила, необходимо упомянуть о проблеме границ. При выполнении некоторого действия могут изменяться другие предикаты и для этого могут использоваться аксиомы границ - правила, определяющие инвариантные предикаты. Одно из решений этой проблемы предложено в системе STRIPS.
В начале 1970-х годов в Стэнфордском исследовательском институте (Stanford Research Institute Planning System) была создана система STRIPS для управления роботом. В STRIPS четыре оператора pickup, putdown, stack, unstack описываются тройками элементов. Первый элемент тройки - множество предусловий ( П ), которым удовлетворяет мир до применения оператора. Второй элемент тройки - список дополнений ( Д ), которые являются результатом применения оператора. Третий элемент тройки - список вычеркиваний ( В ), состоящий из выражений, которые удаляются из описания состояния после применения оператора.
Ведя рассуждения для рассматриваемого примера от начального состояния, мы приходим к поиску в пространстве состояний. Требуемая последовательность действий (план достижения цели) будет следующей:
unstack(A,B), putdown(A), pickup(C), stack(C,B)
Для больших графов (сотни состояний) поиск следует проводить с использованием оценочных функций. Более подробно о работах по планированию, в том числе современные публикации по адаптивному планированию, можно прочитать в литературе [ 1.6 ] , [ 3.3 ] , [ 3.4 ] , [ 3.5 ] , [ 3.6 ] .
В качестве заключения по данному разделу лекции следует сказать, что планирование достижения цели можно рассматривать как поиск в пространстве состояний. Для нахождения пути из начального состояния к целевому ( плана последовательности действий робота ) могут применяться методы поиска в пространстве состояний с использованием исчисления предикатов.
Поиск решений в системах продукций
Поиск решений в системах продукций наталкивается на проблемы выбора правил из конфликтного множества, как это указывалось в предыдущей лекции. Различные варианты решения этой проблемы рассмотрим на примере ЭСО CLIPS, на которой нам предстоит в 7 лекции разработать исследовательский прототип ЭС. Правила в ЭС, кроме фактора уверенности эксперта, имеют приоритет выполнения (salience). Конфликтное множество (КМ) - это список всех правил, имеющих удовлетворенные условия при некотором, текущем состоянии списка фактов и объектов и которые еще не были выполнены. Как отмечалось ранее, конфликтное множество это простейшая база целей. Когда активизируется новое правило с определенным приоритетом, оно помещается в список правил КМ ниже всех правил с большим приоритетом и выше всех правил с меньшим приоритетом. Правила с высшим приоритетом выполняются в первую очередь. Среди правил с одинаковым приоритетом используется определенная стратегия.
CLIPS поддерживает семь стратегий разрешения конфликтов.
Стратегия глубины (depth strategy) является стратегией по умолчанию (default strategy) в CLIPS. Только что активизированное правило помещается поверх всех правил с таким же приоритетом. Это позволяет реализовать поиск в глубину.
Стратегия ширины (breadth strategy) - только что активизированное правило помещается ниже всех правил с таким же приоритетом. Это, в свою очередь, реализует поиск в ширину.
LEX стратегия - активация правила, выполненная более новыми образцами (фактами), располагается перед активацией, осуществленной более поздними образцами. Например, как это указано в таблица 3.3 ниже.
MEA стратегия - сортировка образцов не производится, а осуществляется только упорядочение правил по первым образцам, как это показано в столбце 3 таблица 3.3.
Стратегия упрощения (simplicity strategy) - среди всех правил с одинаковым приоритетом только что активизированное правило располагается выше всех правил с равной или большей определенностью (specificity). Определенность правила задается количеством сопоставлений в левой части правил плюс количество вызовов функций. Логические функции не увеличивают определенность правила.
Стратегия усложнения (complexity strategy) - среди всех правил с одинаковым приоритетом только что активизированное правило располагается выше всех правил с равной или большей определенностью.
Случайная стратегия (random strategy) - каждой активации назначается случайное число, которое используется для определения местоположения среди активаций с определенным приоритетом.
Подход на основе стратегий поиска решений в продукционных ЭС известен достаточно давно. Весьма популярная в начале 90-х годов ЭСО GURU (ИНТЕР-ЭКСПЕРТ) также использовала подобные механизмы управления стратегиями поиска. Возможность смены стратегии в ходе решения задачи программным образом и накопление опыта, какие стратегии дают лучшие результаты для определенных классов задач, позволяет получить эффективные механизмы поиска решений в СПЗ на основе продукций.
Завершая данную лекцию, следует отметить, что существуют различные методы поиска решений в семантических сетях, например, метод обхода семантической сети - мультипарсинг. Данный метод оригинален тем, что позволяет параллельно "вести" по графу несколько маркеров и, тем самым, распараллеливать процесс поиска информации в семантической сети, что увеличивает скорость поиска. Эти методы используются, как правило, при представлении текста в виде объектно-ориентированной семантической сети и в данной лекции не рассматриваются.
Поиск в сетях фреймов, основанный на прецедентах вывод (Case-based Reasoning - CBR), правдоподобные рассуждения (plausible reasoning), методы поиска на основе нечеткой логики и другие методы поиска решений ИИ в данной лекции также не рассматриваются из-за ограничений на объем данного учебного пособия. Читателю рекомендуется обратиться к соответствующей литературе [ 3.5 ] , [ 3.6 ] , [ 3.7 ] , [ 3.8 ] , [ 3.9 ] .

